6.6 Q&A

Q: What is stochastic approximation?

A: Stochastic approximation refers to a broad class of stochastic iterative algorithms for solving root-finding or optimization problems.

Q: Why do we need to study stochastic approximation?

A: This is because the temporal-difference reinforcement learning algorithms that will be introduced in Chapter 7 can be viewed as stochastic approximation algorithms. With the knowledge introduced in this chapter, we can be better prepared, and it will not be abrupt for us to see these algorithms for the first time.

Q: Why do we frequently discuss the mean estimation problem in this chapter?

A: This is because the state and action values are defined as the means of random variables. The temporal-difference learning algorithms introduced in Chapter 7 are similar to stochastic approximation algorithms for mean estimation.

Q: What is the advantage of the RM algorithm over other root-finding algorithms?

A: Compared to many other root-finding algorithms, the RM algorithm is powerful in the sense that it does not require the expression of the objective function or its derivative. As a result, it is a black-box technique that only requires the input and output of the objective function. The famous SGD algorithm is a special form of the RM algorithm.

Q: What is the basic idea of SGD?

A: SGD aims to solve optimization problems involving random variables. When the probability distributions of the given random variables are not known, SGD can solve the optimization problems merely by using samples. Mathematically, the SGD algorithm can be obtained by replacing the true gradient expressed as an expectation in the gradient descent algorithm with a stochastic gradient.

Q: Can SGD converge quickly?

A: SGD has an interesting convergence pattern. That is, if the estimate is far from the optimal solution, then the convergence process is fast. When the estimate is close to the solution, the randomness of the stochastic gradient becomes influential, and the convergence rate decreases.

Q: What is MBGD? What are its advantages over SGD and BGD?

A: MBGD can be viewed as an intermediate version between SGD and BGD. Compared to SGD, it has less randomness because it uses more samples instead of just one as in SGD. Compared to BGD, it does not require the use of all the samples, making it more flexible.

Chapter 7

Temporal-Difference Methods

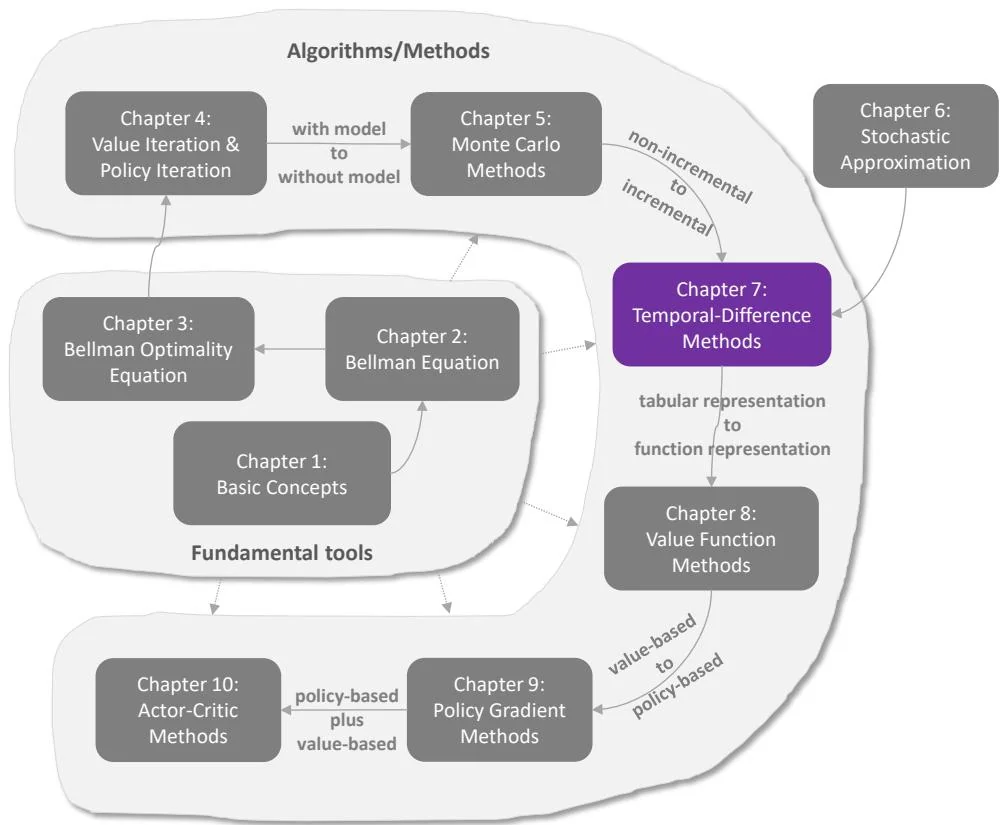
Figure 7.1: Where we are in this book.

This chapter introduces temporal-difference (TD) methods for reinforcement learning. Similar to Monte Carlo (MC) learning, TD learning is also model-free, but it has some advantages due to its incremental form. With the preparation in Chapter 6, readers will not feel alarmed when seeing TD learning algorithms. In fact, TD learning algorithms can be viewed as special stochastic algorithms for solving the Bellman or Bellman optimality equations.

Since this chapter introduces quite a few TD algorithms, we first overview these algorithms and clarify the relationships between them.

$\diamond$ Section 7.1 introduces the most basic TD algorithm, which can estimate the state

values of a given policy. It is important to understand this basic algorithm first before studying the other TD algorithms.

$\diamond$ Section 7.2 introduces the Sarsa algorithm, which can estimate the action values of a given policy. This algorithm can be combined with a policy improvement step to find optimal policies. The Sarsa algorithm can be easily obtained from the TD algorithm in Section 7.1 by replacing state value estimation with action value estimation.
$\diamond$ Section 7.3 introduces the $n$ -step Sarsa algorithm, which is a generalization of the Sarsa algorithm. It will be shown that Sarsa and MC learning are two special cases of $n$ -step Sarsa.
$\diamond$ Section 7.4 introduces the Q-learning algorithm, which is one of the most classic reinforcement learning algorithms. While the other TD algorithms aim to solve the Bellman equation of a given policy, Q-learning aims to directly solve the Bellman optimality equation to obtain optimal policies.
$\diamond$ Section 7.5 compares the TD algorithms introduced in this chapter and provides a unified point of view.