13.1 定义与变形

包容性扫描（inclusive scan）需要一个符合结合律的二元操作符和长度为N的数组

并返回如下数组

可以看出，输出的每个元素依赖于输入中前一位置元素。

排他性扫描（exclusive scan）被类似地定义，但对输出作了移位，并使用一个单位元素id⊕（单位元素同某个值执行操作符⊕的运算，不会对这个值产生任何改变，例如，0为整数加法的单位元素，1为乘法的单位元素等）。

包容性和排他性扫描可以通过依次添加或减去输入数组的元素而相互转化，如图13-1所示。

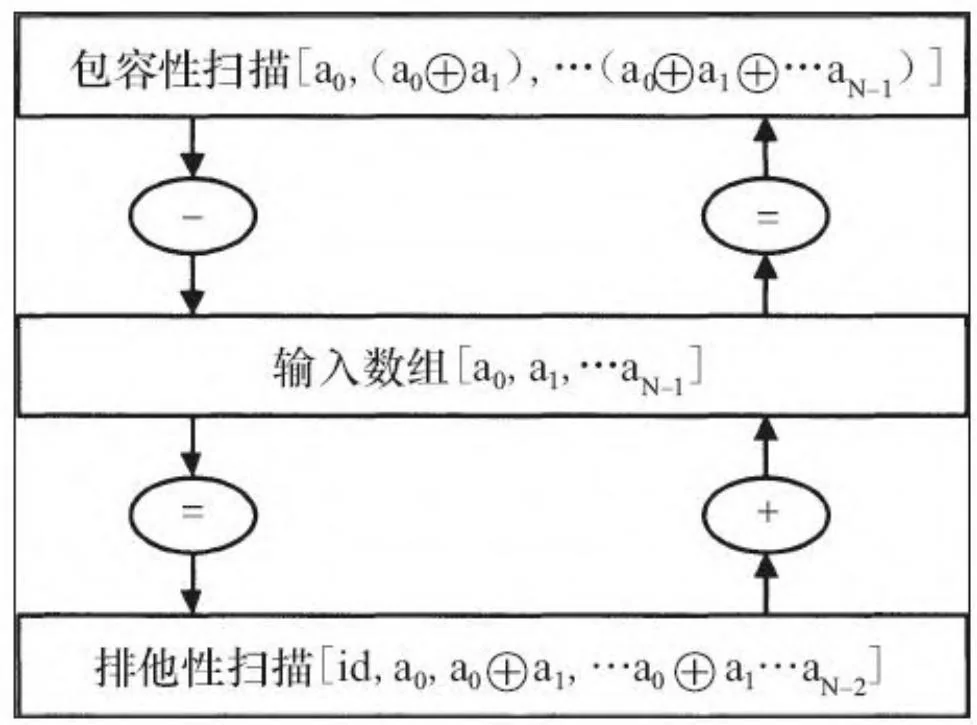
图13-1 包容性和排他性扫描

流压缩是根据一定标准提取数组中元素的操作。如果一个断定（0或1）被用于判断输入数组的每个元素是否应该包含在输出流中，那么接着可以按照此断定执行一个排他性扫描来计算输出的元素的索引。一个流压缩的变形，被称为流拆分，按照每个断定值独立的写回紧凑的输出。分段扫描（segmented scan）也是一种变形。它在输入数组的基础上配有一组输入标志（每个数组元素对应一个标志），并在由标志分割的子阵列上执行扫描。

鉴于扫描原语的重要性，在实现优化的CUDA扫描算法方面，已投入了大量努力。在本章结尾处，提供了一个参考文献列表。无论是CUDPP，还是Thrust库，都包括一组优化了的扫描原语，它们使用模板

达到通用性和性能之间的最佳折衷。然而，总体而言，使用扫描原语的应用程序通常能够从“充分利用了具体问题的领域知识的自定义实现”中获益。