13.2 概述

一个简单的 $\mathrm{C}++$ 实现如代码清单13-1所示。

代码清单13- 1 包容性扫描代码（C++）

template<class T> T InclusiveScan(T *out, const T *in, size_t N) {
    T sum(0);
    for (size_t i = 0; i < N; i++) {
        sum += in[i];
        out[i] = sum;
    }
    return sum;
}

对于代码清单13-1和13-2这些串行实现，包容性和排他性扫描之间的唯一区别在于如下行

代码清单13-2 排他性扫描代码（C++）

out[i] = sum;

和

sum  $+ =$  in[i];

作了交换。 [1]

template<class T>  
T ExclusiveScan(T *out, const T *in, size_t N)  
{  
    T sum(0);  
    for (size_t i = 0; i < N; i++) {  
        out[i] = sum;  
        sum += in[i];  
    }  
    return sum;

扫描的串行实现是如此显而易见而又微不足道，如果你拿不准它的并行实现，是可以理解的！所谓的前缀依赖性，即其中每个输出依赖于前面的所有输入。由于扫描的前缀依赖性，可能有些人甚至会怀疑它是否能够并行。但是，经过思考，你可以看到，相邻两个数的操作（ $\mathrm{a}_{i} \oplus \mathrm{a}_{i+1} 0 \leqslant i < N-1$ ）可以并行的计算，对于 $i=0$ ， $\mathrm{a}_{i} \oplus \mathrm{a}_{i+1}$ 计算扫描的最终输出，否则，这些针对一对数的操作计算部分和，并在后面归入最终输出，就像我们在第12章中那样使用部分和。

Blelloch [2] 描述了一个两遍算法。其中自底向上阶段（upsweep phase）计算数组的归约，并依次存储中间结果；随后的自顶向下阶段（downsweep phase）计算扫描的最终输出。自底向上阶段的伪代码如下。

upswep(a,N) for d from 0 to (1g N)-1 in parallel for i from 0 to N-1 by  $2^{0 - 1}$  a[i+2²i-1] +=a[i+2d-1]

该操作类似于之前讨论过的对数步长的归约，不同之处在于部分和要存储起来，以备后面用到产生扫描的最终输出中去。

按照Blelloch的方法，图13-2显示了一个使用该自底向上代码运行的例子，该例子对8个元素构成的数组施行整数加法运算。“自底向上”这一术语源于将数组看作一颗平衡树（见图13-3）。

一旦完成自底向上阶段，一个自顶向下阶段把“中间和”传播到树的叶子。自顶向下阶段的伪码如下。

downsweep(a, N)  
a[N-1] = 0  
for d from (lg N)-1 downto 0  
in parallel for i from 0 to N-1 by  $2^{d-1}$   
t := a[i+2^d-1]  
a[i+2^d-1] = a[i + 2^{d+1}-1]  
a[i+2^{d+1}-1] += t

步骤

0 3 1 7 0 4 1 6 3
1 3 4 7 7 4 5 6 9
2 3 4 7 11 4 5 6 14
3 4 7 11 4 5 6 25

图13-2 自底向上阶段（数组视图）

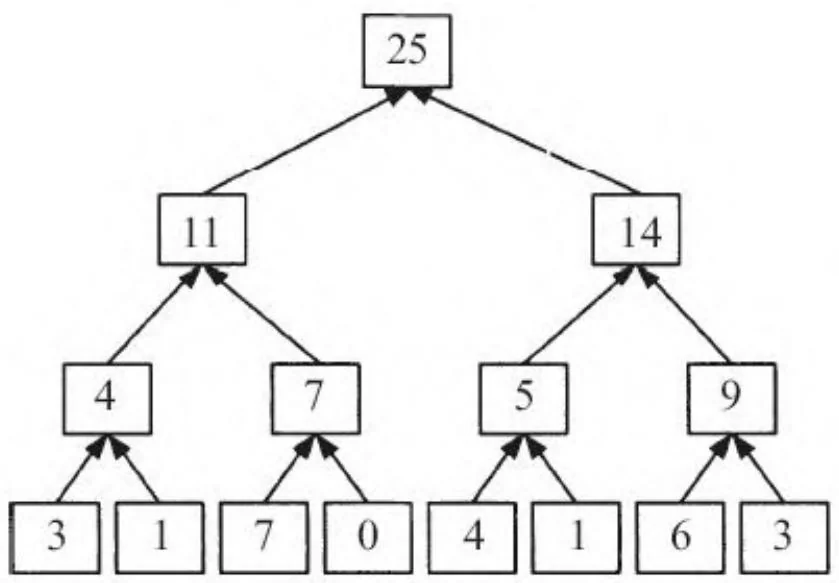
图13-3 自底向上阶段（树视图）

图13-4显示了示例数组是如何在自顶向下阶段进行转化的，而图13-5以树的形式显示了自顶向下阶段的过程。CUDA早期实现的扫描算法紧密遵循了这一算法，而且它在促使大家思考扫描算法的实现上起到了很好的作用。遗憾的是，这一算法跟CUDA架构的匹配存在瑕疵，简单地实现它会导致共享内存的存储片冲突，并且为了弥补冲突而使用的寻址方案，会导致得不偿失的开销。

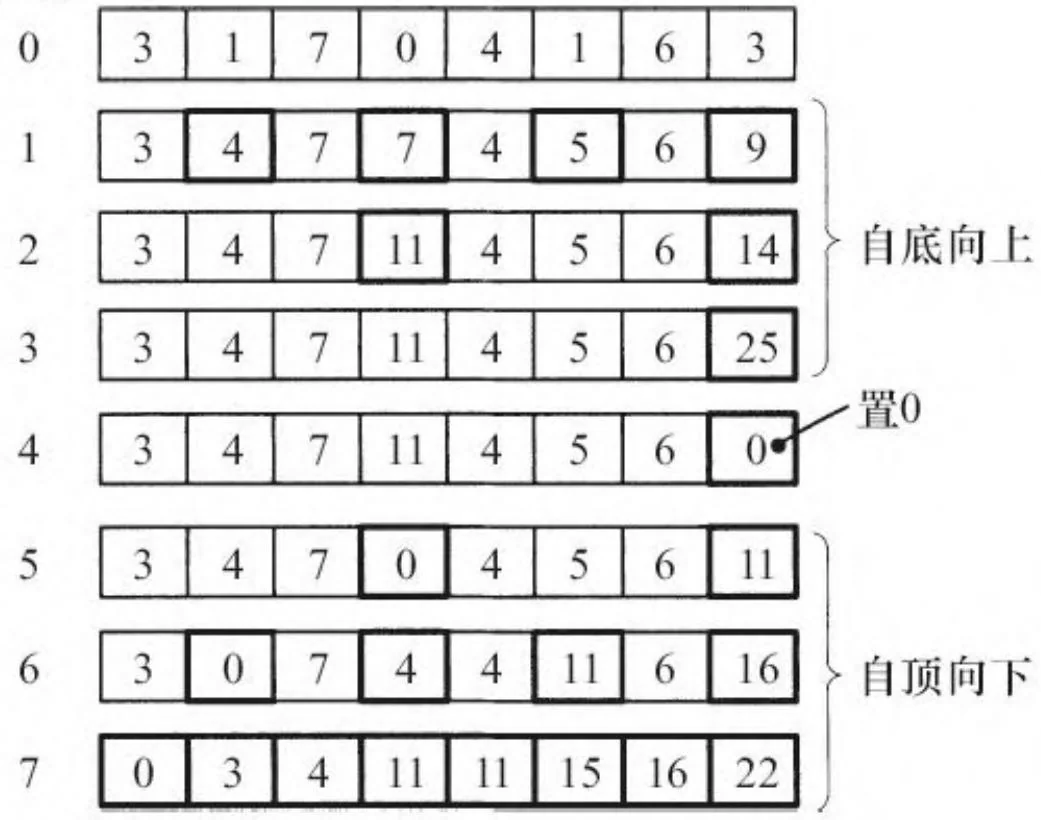
步骤

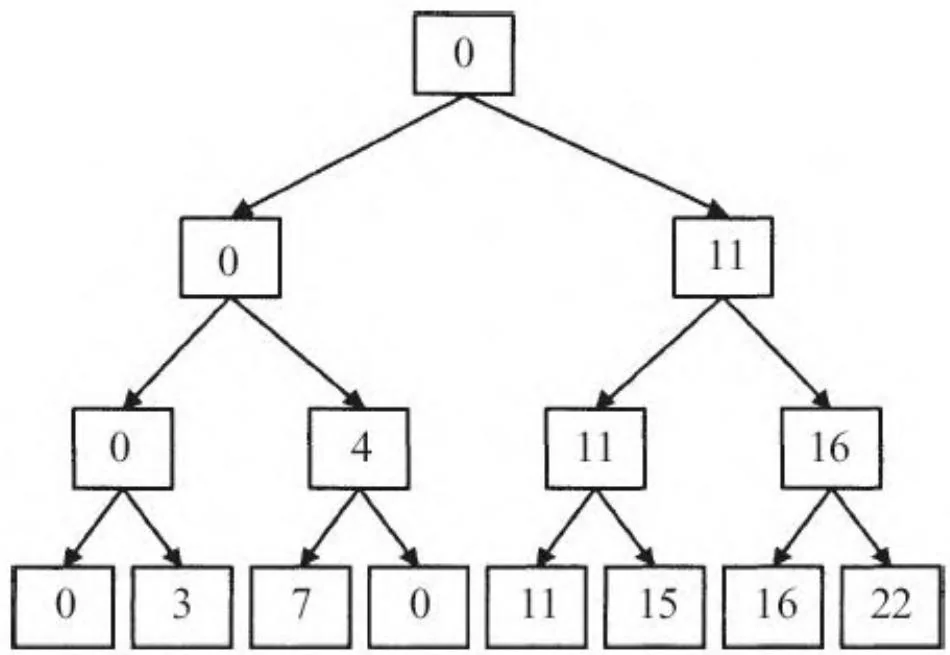
图13-4 自顶向下阶段（数组视图）
图13-5 自顶向下阶段（树视图）

[1] 成书之际，排他性扫描的实现还不支持原地计算（in-place computation）。为了让输入和输出数组保持不变，in[i]必须保存到一个临时变量中。
[2] http://bit.ly/YmTmGP。