10.5 使用非归一化坐标的纹理操作

除了tex1Dfetch()，其他所有的纹理指令均使用浮点值指定纹理中的坐标位置。当使用非归一化的纹理坐标时，坐标的范围将为[0,MaxDim)，其中MaxDim表示纹理的宽度、高度或深度。非归一化的坐标是一种按符合人类直觉的方式对纹理进行索引的方式，使用该坐标时许多纹理特性将变得不可用。

研究纹理操作行为的一种简单方式就是将纹理中的每个元素填充为该纹理的索引值。图10-4显示的一个浮点值类型且只有16个元素的一维纹理。图中使用标识元素填充每个纹理，图的下方还注释了部分使用tex1D()得到的返回值。

尽管使用非归一化的纹理坐标时，会导致部分纹理操作特性不可用，但若结合线性过滤以及有限形式的纹理寻址模式，也可使用这些纹理特性。纹理寻址模式指明了硬件如何处理超出范围的纹理坐标的方式。图10-4显示了：针对于非归一化的坐标，在从纹理获取数据之前，将范围夹取在[0,MaxDim）之间的默认纹理寻址模式。图中值16.0超出了范围，通过夹取，获取的值为15.0。当使用非归一化的坐标时，还可以使用另一种称为边缘寻址模式的纹理寻址选项，即超出范围的坐标对应的返回值为零。

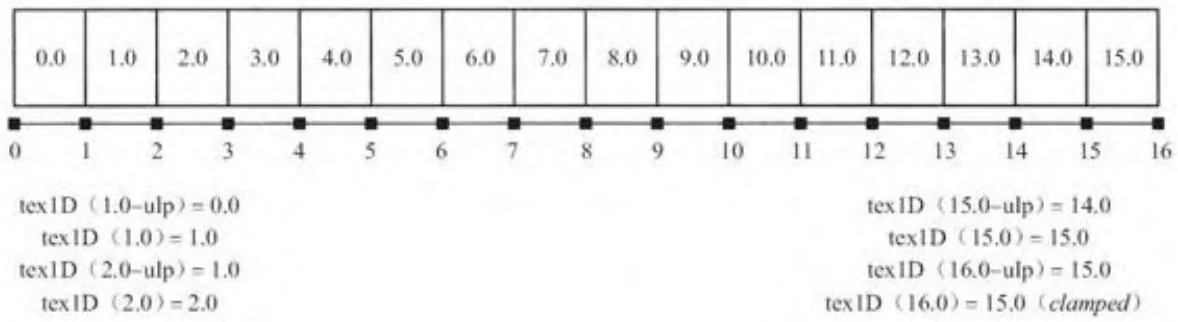
图10-4 使用非归一化坐标进行纹理操作（不包含线性过滤）

过滤模式默认使用的是“点过滤”，其根据浮点坐标值返回一个纹理元素。相反，线性过滤将使纹理硬件获取相邻的两个纹理元素，并在它们之间根据纹理坐标作为权重进行线性插值。图10-5显示了含16个元素的一维纹理，附有返回自tex1D()的若干样例值。注意，纹理坐标必须加上0.5才能获得标识元素。

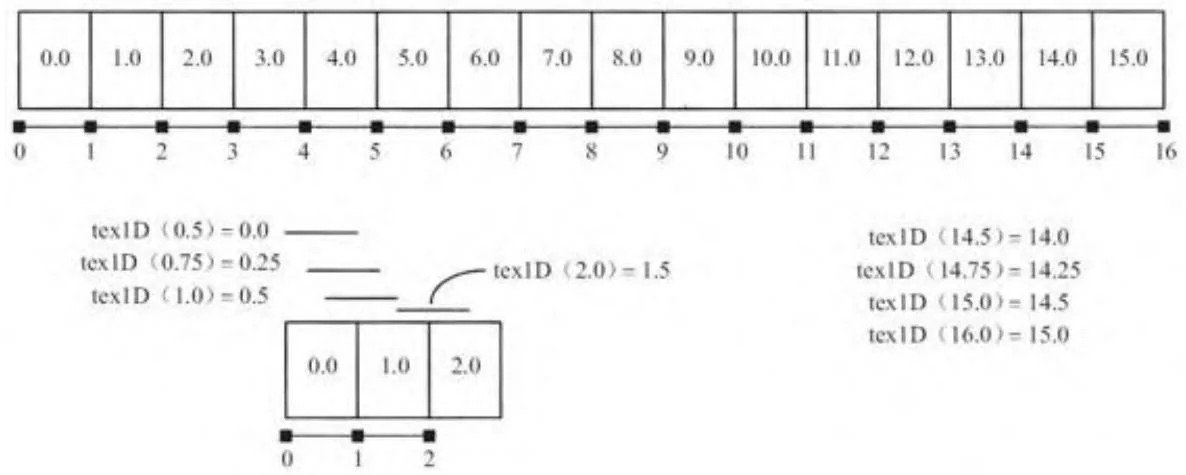
图10-5 使用非归一化纹理坐标的纹理操作（线性过滤模式）

许多纹理操作特性可以相互结合使用，例如，线性过滤可以与之前讨论的整型增强为浮点型的操作结合使用。若这样使用，指令

tex1D()将返回根据相邻两个增强的浮点纹理元素进行插值之后的精确结果。

程序演示：tex1d_unnormalized.cu

程序texld_unnormalized.cu就像一个显微镜，通过打印出纹理坐标以及对应tex1D()的返回值仔细的检视纹理操作。与程序texldfetch_int3float.cu不同，该程序的纹理数据使用的是一维CUDA数组存储的。该程序根据指定的基地址与增量，在一定浮点数范围内执行了一系列的纹理读取操作，并将插值得到的值与tex1D()的返回值一起保存到float2类型的输出数组中。以下是该CUDA内核的源代码。

texture<float, 1> tex;
extern "C" __global__void
TexReadout(float2 *out, size_t N, float base, float increment)
{
    for (size_t i = BlockIdx.x*blockDim.x + threadIdx.x; i < N; i++)
        gridDim.x*blockDim.x)
    {
        float x = base + (float) i * increment;
        out[i].x = x;
        out[i].y = tex1D.tex, x);
    }
}

代码清单10-4列出了一个主机端函数CreateAndPrintTex()的代码，该函数接受将要创建的纹理的大小、执行纹理采样操作的次数、将传给tex1D()的浮点范围基地址和增量以及两个可选的纹理过滤和寻址方式等几个参数。函数创建了保存纹理数据的CUDA数组，然后根据调用者的需要，可以选择将该数组初始化为调用者提供的数据（若调

用者传递的值为NULL则初始化为标识元素），接着函数将纹理绑定到 CUDA数组上，最后打印float2类型的输出数组。

代码清单10-4 CreateAndPrintTex()

template<class T>   
void   
CreateAndPrintTex(T \*initTex,size_t texN,size_t outN, float base,float increment, CUDATextureFilterMode filterMode  $=$  CUDAFilterModePoint, CUDATextureAddressMode addressMode  $=$  CUDAAddressModeClamp ） { T\*texContents  $= 0$  . CUDAArray \*texArray  $= 0$  ： float2 \*outHost  $= 0$  \*outDevice  $= 0$  . CUDAError_t status; CUDAChannelFormatDesc channelDesc  $=$  CUDACreateChannelDesc<T>(); //use caller-provided array，if any,to initialize texture if（initTex）{ texContents  $\equiv$  initTex; } else{ //default is to initialize with identity elements texContents  $=$  (T\*) malloc( texN\*sizeof(T)); if（！texContents） goto Error; for（int i  $= 0$  ;i< texN；i++）{ texContents[i]  $\equiv$  (T)i; 1 CUDART_CHECK(cudaMallocArray(&texArray,&channelDesc,texN)); CUDART_CHECK(cudaHostAlloc(void \*\*)&outHost, outN\*sizeof(float2), CUDAHostAllocMapped); CUDART_CHECK(cudaHostGetDevicePointer( (void \*\*) &outDevice, outHost,0));

CUDART_CHECK(cudaMemcpyToArray( texArray, 0, 0, texContents, texN*sizeof(T), CUDAMemcpyHostToDevice)); CUDART_CHECK(cudaBindTextureToArrayTEX, texArray)); tex.filterMode  $=$  filterMode; tex-addressMode[0]  $\equiv$  addressMode; CUDART_CHECK(cudaHostGetDevicePointer(&outDevice,outHost,0)); TexReadout<<2,384>>>(outDevice,outN-base,increment); CUDART_CHECK(cudaThreadSynchronize()); for (int i = 0; i < outN; i++) { printf("%.2f,%.2f)\n",outHost[i].x,outHost[i].y); } printf("\n"); Error: if(!initTex) free(texContents); if (texArray)cudaFreeArray(texArray); if(outHost)cudaFreeHost(outHost); }

该程序的main()函数可以通过修改来帮助我们更好的理解纹理操作的行为。当前版本的main()函数创建了一个包含8个元素的纹理，并打印出tex1D()的输出值，范围从 $0.0 \sim 7.0$ 。

int   
main(int argc, char \*argv[])   
{ CUDA_ERROR_t status; CUDA_CHECK(cudaSetDeviceFlags(cudaDeviceMapHost)); CreateAndPrintTex(float>NULL,8,8,0.0f,1.0f); CreateAndPrintTexfloat>NULL,8,8,0.0f,1.0f, CUDAFilterModeLinear); return 0;

该程序的输出结果如下所示：

(0.00, 0.00)  
(1.00, 1.00)  
(2.00, 2.00)  
(3.00, 3.00)  
(4.00, 4.00)  
(5.00, 5.00)  
(6.00, 6.00)  
(7.00, 7.00)  
(0.00, 0.00)  
(1.00, 0.50)  
(2.00, 1.50)  
(3.00, 2.50)  
(4.00, 3.50)  
(5.00, 4.50)  
(6.00, 5.50)  
(7.00, 6.50)

如果将main()函数按以下方式修改函数CreateAndPrintTex()的调用方式，

CreateAndPrintTex<float>(NULL, 8, 20, 0.9f, 0.01f, CUDAFilterModePoint);

从输出的结果可以看出，当使用点过滤模式时，1.0是0号纹理元素与1号纹理元素的分界线。

(0.90, 0.00)  
(0.91, 0.00)  
(0.92, 0.00)  
(0.93, 0.00)  
(0.94, 0.00)  
(0.95, 0.00)  
(0.96, 0.00)  
(0.97, 0.00)  
(0.98, 0.00)  
(0.99, 0.00)  
(1.00, 1.00)  
(1.01, 1.00)  
(1.02, 1.00)  
(1.03, 1.00)  
(1.04, 1.00)  
(1.05, 1.00)  
(1.06, 1.00)  
(1.07, 1.00)  
(1.08, 1.00)  
(1.09, 1.00)

线性过滤的一个限制就是使用9位的权重因子。注意，插值的精度不是依赖于纹理元素的精度而是权重。以一个10元素的纹理为例，纹

理元素初始化为归一化的标识元素，即用（0.0,0.1,0.2,0.3…0.9）代替（0,1,2…9），CreateAndPrintTex()函数可以指定纹理内容，因此可以按照以下代码进行操作：

float texData[10];   
for（int  $\mathrm{i} = 0$  ：i<10；i++）{ texData[i]  $=$  (float)i/10.of; } CreateAndPrintTex<float>(texData，10,10,0.0f,1.0f）;

调用未修改的CreateAndPrintTex()得到的输出，改变并不大。

(0.00, 0.00)  
(1.00, 0.10)  
(2.00, 0.20)  
(3.00, 0.30)  
(4.00, 0.40)  
(5.00, 0.50)  
(6.00, 0.60)  
(7.00, 0.70)  
(8.00, 0.80)  
(9.00, 0.90)

若想让CreateAndPrintTex()在头两个元素（值为0.1和0.2）之间进行线性插值，则需要改为如下所示的代码：

CreateAndPrintTex<float>(tex,10,10,1.5f,0.1f,cudaFilterModelLinear);

得到的输出结果如下所示:

(1.50, 0.10)  
(1.60, 0.11)  
(1.70, 0.12)  
(1.80, 0.13)  
(1.90, 0.14)  
(2.00, 0.15)  
(2.10, 0.16)  
(2.20, 0.17)  
(2.30, 0.18)  
(2.40, 0.19)

通过截断为2位小数部分，得到的数据看起来表现很好。但若将CreateAndPrintTex()的输出改为十六进制，则输出结果将变为

(1.50, 0x3dcccccd)  
(1.60, 0x3de1999a)  
(1.70, 0x3df5999a)  
(1.80, 0x3e053333)  
(1.90, 0x3e0f3333)  
(2.00, 0x3e19999a)  
(2.10, 0x3e240000)  
(2.20, 0x3e2e0000)  
(2.30, 0x3e386667)  
(2.40, 0x3e426667)

很明显，大多数十进制小数无法准确描述为浮点数。不过，尽管执行插值操作时不需要过高的精度，这些值仍是以全精度（full precision）进行插值的。

程序演示：tex1d_9bit.cu

为了进一步了解精度问题，我们编写了另一个程序演示texld_9bit.cu。该程序中，纹理将以32位的浮点数填充，每个浮点数必须以全精度才能正确表示。若以全精度进行插值操作，程序中除了传递纹理坐标的基地址和增量这对参数外，还需要传递另一对参数，即“期待”插入的值的基地址和增量。

在程序tex1d_9bit.cu中，函数CreateAndPrintTex()被修改为代码清单10-5中所示的代码以打印输出结果。

代码清单10-5 texld_9bit.cu（节选）

printf("X\tY\tActual Value\tExpected Value\tDiff\n");   
for (int i = 0; i < outN; i++) { T expected; if (bEmulateGPU) { float x = base + (float)i*increment - 0.5f; float frac = x - (float) (int) x; int frac256 = (int) (frac*256.0f+0.5f); frac = frac256/256.0f; } int index = (int) x; expected = (1.0f-frac)*initTex[index] + frac*initTex[index+1]; } else { expected = expectedBase + (float) i*expectedIncrement; float diff = fabsf(outHost[i].y - expected); printf("%2f\t%.2f\t",outHost[i].x,outHost[i].y); printf("%08x\t",*(int*)(&outHost[i].y)); printf("%08x\t",*(int*)(&expected)); printf("%E\n",diff); } printf("\n");

对之前包含10个值的纹理（以0.1递增），可以把调用该函数产生的真实纹理结果与预期的全精度结果进行对比。函数的调用为：

CreateAndPrintTex<float>(tex, 10, 4, 1.5f, 0.25f, 0.1f, 0.025f); CreateAndPrintTex<float>(tex, 10, 4, 1.5f, 0.1f, 0.1f, 0.01f);

得到的输出为:

X Y Actual Value Expected Value Diff 1.50 0.10 3dcccccd 3dcccccd 0.000000E+00 1.75 0.12 3e00000 3e00000 0.000000E+00 2.00 0.15 3e1999a 3e1999a 0.000000E+00 2.25 0.17 3e33333 3e33333 0.000000E+00 X Y Actual Value Expected Value Diff 1.50 0.10 3dcccccd 3dcccccd 0.000000E+00 1.60 0.11 3de1999a 3de147ae 1.562536E-04 1.70 0.12 3df5999a 3df5c290 7.812679E-05 1.80 0.13 3e053333 3e051eb8 7.812679E-05

通过输出结果中最右侧的“Diff”列可以看出，第一组输出均是以全精度插值的，而第二组的则不是。《CUDA编程指南》一书的附录F解释了产生这种差别的原因，给出了一维纹理的线性插值公式：

$\operatorname{tex}(\mathrm{x}) = (1 - \alpha) \mathrm{T}(\mathrm{i}) + \alpha \mathrm{T}(\mathrm{i} + 1)$

这里

$\mathrm{i} = \text{floor}(\mathrm{X}_{\mathrm{B}})$ ,  $\mathrm{a} + \text{frac}(\mathrm{X}_{\mathrm{B}})$ ,  $\mathrm{X}_{\mathrm{B}} = \mathrm{x} - 0.5$

其中 $\alpha$ 保存了一个9位的定点值，它使用8位表示小数部分。

代码清单10-5中，该公式是基于bEmulateGPU的值分别模拟的。texld_9bit.cu中可以通过将函数CreateAndPrintTex()中的参数bEmulateGPU值设置为true，从而模拟9位的权重值。相应得到的输出如下所示：

X Y Actual Value Expected Value Diff  
1.50 0.10 3dcccccd 3dcccccd 0.000000E+00  
1.75 0.12 3e00000 3e00000 0.000000E+00  
2.00 0.15 3e19999a 3e19999a 0.000000E+00  
2.25 0.17 3e33333 3e33333 0.000000E+00  
X Y Actual Value Expected Value Diff  
1.50 0.10 3dcccccd 3dcccccd 0.000000E+00  
1.60 0.11 3de1999a 3de1999a 0.000000E+00  
1.70 0.12 3df5999a 3df5999a 0.000000E+00  
1.80 0.13 3e053333 3e053333 0.000000E+00

从最右栏的一列0中可以看出，当采用9位的精度计算插值时，预期值与真实值之间不再存在差异。