8.3_浮点支持

8.3 浮点支持

快速的本地浮点硬件是GPU一大优势，而且在许多方面，它们都等同于或优于CPU的浮点实现。可以全速支持非归一化的浮点数，[1]可在每一条指令级别执行定向舍入操作，并提供特殊函数单元，支持高性能的近似6种流行的单精度超越函数。相比之下，对非归一化的浮点数，x86 CPU执行它们的微码可能会比归一化浮点指令慢100倍。取整方向由一个控制字指定，改变取整方向可能需要几十个时钟周期，SSE指令集中唯一的超越近似函数是取倒数和平方根倒数，且仅提供12位的近似结果，必须使用牛顿-拉夫逊迭代完善后方可使用。

由于受其较低的时钟频率影响，GPU在核心数量上的优势有所抵消，在相同的条件下开发者可以预期10倍（左右）加速。如果有论文指出从优化的CPU实现移植到CUDA会产生100倍或更大的加速，很可能是以上描述的“指令集不匹配”的原因。

8.3.1 格式

CUDA支持图8-1所示的3种IEEE标准浮点格式：双精度（64位）、单精度（32位）和半精度（16位）。每1个数被分成3个字段：符号、指数和尾数。


图8-1 浮点数格式

对于双精度、单精度和半精度来说，指数位数分别为11、8和5位，相应的尾数位数分别是52、23和10位。

指数字段更改了浮点数的解释方式。最常见的（“归一化”）编码表示是，对尾数加入一个隐含“1”位并用尾数乘以 2e−bias2^{e - bias} ，其中 bias 是在编码为浮点数表示之前加入到实际指数值的偏移。例如，bias 对于单精度来说是 127。

表8-7总结了浮点值如何进行编码。大多数指数值（即“归一化”的浮点值），假定尾数有一个隐含的“1”，并将它乘以偏移后的指数值。最大指数值被保留为无穷大和NaN（Not A Number）值。被0除（或除数溢出）结果为无限大；执行无效操作（如使用负数的平方根或对数）会产生一个NaN。最小的指数值为那些非常小的数保留，这些数无法用隐含的首位“1”格式表示。随着非归一化浮点数[2]趋向

零，它们失去了有效位的精度，这种现象被称为渐近下溢。表8-8给出了3种格式的某些临界值的编码和具体值。

表8-7 浮点数的表示

表8-8 浮点数的临界值

1. 舍入

IEEE标准提供四种舍入模式。

·舍入到最近偶数（也称为“最近舍入”）
·向0舍入（也被称为“截断”或“斩断”）
·向下舍入（或“向负无穷大舍入”）

向上舍入（或“向正无穷大舍入”）

最近舍入是中间值四舍五入到每次操作后最接近的可表示的浮点数值，是迄今为止最常用的舍入模式。向上舍入和向下舍入（“定向舍入模式”），用于区间算术，其中一对浮点值是用来界定一个计算的中间结果。要正确界定结果，区间的下限和上限的值必须分别向负无穷大（“向下”）和向正无穷大（“向上”）舍入。

C语言没有为每条指令提供任何方式来指定舍入模式，而且CUDA硬件也没有提供一个可以隐式指定舍入模式的控制字。因此，CUDA提供了一套内置函数来指定一个操作的舍入模式，见表8-9。

表8-9 舍入操作的内置函数

2.转换

一般而言，开发者可以在不同的浮点表示和整型之间使用标准C语言的转换：隐式的或显式的类型转换。然而，如果需要的话，开发者

可以使用表8-10中列出的函数来执行转换，这些转换不属于C语言标准，例如，它们涉及定向取整的函数。

因为half不是标准C语言的类型，CUDA使用unsigned short作为函数__half2float()和__float2half()的接口。其中__float2half()只支持最近舍入模式。

float half2float(unsigned short); unsigned short float2half(float);

表8-10 转换函数

8.3.2 单精度（32位）

单精度浮点支持是GPU计算的主力所在。GPU做了许多优化，以在传输这种数据类型上拥有很高的性能表现[3]，不仅仅表现在进行核

心的IEEE标准操作，例如加和乘，还表现在不标准的操作，像sin()和log()这类超越函数的近似。32位浮点数存储在与整型值相同的寄存器中，所以在单精度浮点数与整型之间的转换（使用_float_as_int()和_int_as_float()）是非常轻松的。

1. 加、乘和乘加

编译器会自动的将应用在浮点数上的操作符+、-和*翻译为加、乘和乘加指令。函数__fadd_rn()和__fmul_rn()可以被用来支持将加法和乘法操作转换为乘加指令。

2. 倒数与除

对于计算能力2.x或更高的机器，使用选项--prec-div=true编译会使除法运算符遵从IEEE标准。对于计算能力1.x或者使用编译选项--prec-div=false的计算能力为2.x的机器，除法操作符和 __fdividef(x,y)有着相同精度，但是对于 2126<y<21282^{126} < y < 2^{128} ，函数 __fdividef(x,y)会得到0，而除操作符会得到正确结果。同样，对于 2126<y<21282^{126} < y < 2^{128} ，如果x为无穷大，__fdividef(x,y)返回一个NaN，而除法操作符返回无穷大。

3. 超越函数（SFU）

SM中的特殊函数单元（Special Function Unit，SFU）实现了6种常用的超越函数，并且函数的运算速度非常快。

·正弦与余弦
对数与指数
·倒数与平方根倒数

表8-11节选自关于特斯拉架构的一篇论文 [4]，这篇论文总结了特斯拉架构支持的操作和兼容的精度。SFU并没有实现全精度，但是合理的近似了这些函数的结果，并取得了很好的运行速度。对于大多数依赖SFU运算的代码，CUDA可以远远的领先于优化的CPU版本的性能表现（25倍或更多）。

表8-11 SFU精度

（续）

SFU通过表8-12中给出的内置函数调用。指定编译器选项--fast-math会让编译器使用兼容的SFU函数替代传统的C函数。

表8-12 SFU内置函数

4. 其他函数

_saturate(x)在x<0时返回0，在x>1时返回1，而x为其他值时返回其本身。

8.3.3 双精度（64位）

在SM1.3（首次在GeForce GTX 280中实现）中添加了对CUDA双精度浮点计算的支持，并在SM 2.0中有了大幅度的提升（功能和性能上）。CUDA硬件支持非归一化双精度浮点数的全速计算，并且，从SM 2.x开始，一个原生的乘加指令（FMAD），兼容IEEE 754c.2008标准，只需要一个指令就可实现取整。除了作为一个有用操作，FMAD使那些可以在牛顿-拉尔逊迭代中聚合的特定函数实现全精度运算。

在单精度操作中，编译器自动地将标准C操作符翻译为乘法、加法和乘加指令。内置函数__dadd_rn()和__dmul_rn()可以用来防止乘和

加运算符合并为乘加指令。

8.3.4 半精度（16位）

半精度拥有5位指数和10位尾数，所以half值拥有足够的高动态域（high dynamic range，HDR）图像精度，并且可以用来存储其他类型中不需要达到float精度的值，例如角度。半精度值的出发点在于节省存储，而不是快速计算，所以硬件仅仅提供与32位浮点数之间的转换指令 [5]。这些指令被包装为函数__halftofloat()和__floattohalf()。

float __halftofloat(unsigned short); unsigned short __floattohalf(float);

这些内置函数使用unsigned short数据类型，因为C语言中没有标准的half浮点类型。

8.3.5 案例分析：float到half的转换

分析float到half之间的转换操作对于理解浮点编码和取整的细节非常有用。因为它是简单的一元操作，我们可以把主要精力集中于编码和取整，而不去被浮点运算的细节和中间表示的精度所分心。

当从float转换为half时，对任意的float，如果太大，以至于half形式表现不了时，正确的输出应为无穷大的half。任意的float值，如果太小，以至于half形式表现不了的（即使是一个非正规half），也应该被取整为0.0。取整为half的0.0值的float为 0x32FFFFFF0\mathrm{x}32\mathrm{FFFFFF} 或 2.98−82.98^{-8} ，最小的取为half的无穷大的float为65520.0。在此区间的float值可以被转化为half：通过传递符号位，重新对指数进行偏移（由于float有8位指数，偏移为127，而half有5位指数，偏移为15），最后取整float尾数值到最近的half尾数值。除非待转换的浮点值恰好落于两个可能输出值的正中间，取整是非常容易理解的。对上述这种势均力敌的情形，IEEE标准制定取整到最近的偶数。在十进制算术运算中，这意味着1.5取整为2.0，而且2.5同样取整为2.0，但0.5取整到0.0。

代码清单8-3展示了float到half转换操作的完整的CUDA硬件实现。变量exp和mag分别存储了输入的指数和“幅度”（magnitude）尾数与指数的符号位都屏蔽掉了。许多操作，像比较与取整操作，可以直接通过参数mag执行，而不必分离指数与尾数。

代码清单8-3中的宏LG MAKE_MASK，根据给定的位计数创建一个掩码：#define LG MAKE_MASK(bits) (1≪≪(1\ll \ll bits)-1)。volatile union使得同一个32位的值既可以当作float又可以当做unsigned int类型来处

理；像*(float*)(&u))这样的使用方式是不可移植的。转换会首先传递符号位，并用掩码将其过滤掉。

在提取幅度和指数后，函数会处理输入float为INF和NaN的特殊情况，并作提前退出处理。注意INF是有符号的，但是NaN是一个典型的无符号值。代码的 50∼8050\sim 80 行夹取输入的float值为half可表现的最小或最大值，并重计算幅度的夹取值。不要被构造f32MinRInfin和f32MaxRf16_zero的代码迷惑住，它们分别是常数0x477ff000和0x32FFFFFF。

程序的其余部分处理了输出的归一化和非归一化情况（输入非归一化的情况在之前的代码做了夹取处理，所以mag对应一个归一化的float）。在这段夹取代码中，f32Minf16Normal是一个常量，值为0x38FFFFFF。

为了构造一个归一化数，必须计算一个新的指数（ 92∼9392\sim 93 行），并且正确移出已经取整的10位尾数到输出。为了构造一个非归一化数，输出的尾数要与隐含的1做OR操作，得到的尾数要根据输入指数的数值进行移位。无论是归一化还是非归一化数，输出尾数的取整由2个步骤完成。取整由恰好比输出的有效低位（LSB）短的一个由1组成的掩码序列实现，如图8-2所示。

这一操作在位12被置为1时将输出的尾数增1。如果所有的输入尾数都为1，溢出会使输出指数正确增加。如果我们添加另外一个1到有效高位（MSB），会用传统的取整模式，即在势均力敌时，取整到最接近的大于真实数的整数。相反，为了实现最近偶数取整，我们在10位输出的有效低位（LSB）被置1的情况下，增加输出的尾数值（见图8-3）。注意这些步骤可以顺序实现，也可以通过许多不同的方式实现。


图8-2 舍入操作的掩码


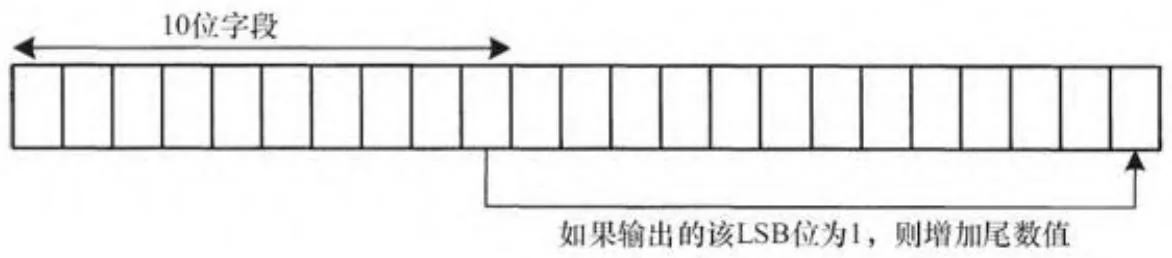
图8-3 舍入到最近偶数（半精度）

代码清单8-3 ConvertToHalf()

$\begin{array}{l}\text{一} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{一} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \\ \text{*} \end{array}$    
const int f16ExpShift  $= 10$  .   
const int f16MantissaBits  $= 10$  ..   
const int f16ExpBias  $= 15$  .   
const int f16MinExp  $= -14$  .   
const int f16MaxExp  $= 15$  .   
const int f16SignMask  $= 0x8000$  ..   
const int f32ExpShift  $= 23$  .   
const int f32MantissaBits  $= 23$  ..   
const int f32ExpBias  $= 127$  ..   
const int f32SignMask  $= 0x80000000$  ..   
unsigned short   
ConvertFloatToHalf(floatf）{ /\* ·Use a volatile union to portably coerce ·32-bit float into 32-bit integer ·/ volatile union { floatf; unsigned int u; }uf; uf.f  $=$  f;   
// return value: start by propagating the sign bit. unsigned short w  $=$  (uf.u >> 16) & f16SignMask; // Extract input magnitude and exponent unsigned int mag  $=$  uf.u & -f32SignMask; int exp  $=$  (int) (mag >> f32ExpShift) - f32ExpBias; // Handle float32 Inf or NaN if（exp  $= =$  f32ExpBias+1）{//INForNaN if（mag&LG MAKE_MASK(f32MantissaBits)) return 0x7fff; // NaN // INF-propagate sign return w|0x7c00;   
/\* ·clamp float32 values that are not representable by float16 /\* if/minfloat32 magnitude that rounds to float16 infinity unsigned int f32MinRInfin  $=$  (f16MaxExp+f32ExpBias)  $<  <  _{\cdot}$  f32ExpShift; f32MinRInfin  $| =$  LG MAKE_MASK( f16MantissaBits+1 ) << (f32MantissaBits-f16MantissaBits-1); if (mag  $>$  f32MinRInfin) mag  $=$  f32MinRInfin;   
1 max float32 magnitude that rounds to float16 0.0
unsigned int f32MaxRf16_zero = f16MinExp + f32ExpBias - (f32MantissaBits - f16MantissaBits - 1); f32MaxRf16_zero <= f32ExpShift; f32MaxRf16_zero |= LG MAKE_MASK(f32MantissaBits); if (mag < f32MaxRf16_zero) mag = f32MaxRf16_zero; } /* * compute exp again, in case mag was clamped above */ exp = (mag >> f32ExpShift) - f32ExpBias; // min float32 magnitude that converts to float16 normal unsigned int f32Minf16Normal = ((f16MinExp + f32ExpBias) << f32ExpShift); f32Minf16Normal |= LG MAKE_MASK(f32MantissaBits); if (mag >= f32Minf16Normal) { // Case 1: float16 normal // Modify exponent to be biased for float16, not float32 mag += (unsigned int) ((f16ExpBias - f32ExpBias) << f32ExpShift); int RelativeShift = f32ExpShift - f16ExpShift; // add rounding bias mag += LG MAKE_MASK(RelativeShift - 1); // round-to-nearest even mag += (mag >> RelativeShift) & 1; w |= mag >> RelativeShift; } else { /* Case 2: float16 denomial // mask off exponent bits - now fraction only mag &= LG MAKE_MASK(f32MantissaBits); // make implicit 1 explicit mag |= (1 << f32ExpShift); int RelativeShift = f32ExpShift - f16ExpShift + f16MinExp-exp; // add rounding bias mag += LG MAKE_MASK(RelativeShift - 1); // round-to-nearest even mag += (mag >> RelativeShift) & 1; w |= mag >> RelativeShift; } return w; }

实际上，开发者应该使用内置函数__floattohalf()将float转换为half，编译器会将其翻译为单条F2F机器指令。这一样例程序只是单

纯的用来解释浮点结构和取整；同样，检查所有的INF/NAN特殊情况和非归一化值的代码，帮助我们展示了“为什么IEEE标准的这些特性从它诞生以来就争议不断”：由于它不仅仅增加了硅的面积，还增加了工程师验证正确性的付出，它使硬件变得更慢、代价更大或者两者兼而有之。

在随同本书一同发布的代码中，代码清单8-3中的程序ConvertFloatToHalf()被整合在程序float_to_float16.cu文件中，并对每一个32位浮点值测试了它的输出。

8.3.6 数学函数库

CUDA包含了一个类似于C语言运行时库的内置数学函数库，但有一些差别：CUDA硬件不包括取整模式寄存器（相反，取整模式由每条指令来编码）[6]。所以，像rint()函数会默认使用最近取整模式。除此之外，硬件不会抛出浮点异常；异常操作的结果，例如对负数取平方根，会被编码为NaN。

表8-13列出了所有的数学函数库函数和每个函数的最大ulp误差。大多数使用float进行运算的函数，会在函数名之后追加一个f，例如，计算正弦函数的函数有：

double sin(double angle); floatsinf(floatangle);

在表8-13中，它们被表示为sin[f]。

表8-13 数学函数

原公式有误，已修正。——译者注

原文把平方根倒数误为倒数，已修改。——译者注

注：*对于贝塞尔函数 jnf(n,x)\mathrm{jnf}(\mathrm{n}, \mathrm{x}) 和 jn(n,x)\mathrm{jn}(\mathrm{n}, \mathrm{x}) ，当 n=128\mathrm{n}=128 时，最大绝对误差分别为 2.2×10−62.2 \times 10^{-6} 和 5×10−125 \times 10^{-12} 。

**对贝塞尔函数 ynf(n,x)\mathrm{ynf}(\mathrm{n},\mathrm{x}) ， ∣x∣|\mathbf{x}| 的误差为 [2+2.5n][2 + 2.5n] ；另一方面，当 n=128n = 128 时最大绝对误差为 2.2×10−62.2 \times 10^{-6} 。对 yn(n,x)\mathrm{yn}(\mathrm{n},\mathrm{x}) ，最大绝对误差为 5×10−125 \times 10^{-12} 。

(1)在SM 1.x硬件上, 合并在FMAD指令中的加和乘指令的精度会因为中间尾数的截断而降低精度。
②在SM 2.x和之后的硬件上，开发者可以通过指定选项--prec-div=true来使误差降低到0ulp。
(3)对float类型， ∣x∣<8|\mathrm{x}| < 8 时误差为9ulp；否则，最大绝对误差为 2.2×10−62.2 \times 10^{-6} 。对double， ∣x∣<8|\mathrm{x}| < 8 的误差为7ulp；否则，最大绝对误差为 5×10−125 \times 10^{-12} 。
④函数lgamma()在区间-10.001,-2.264之间的误差大于6。lgamma()在区间-11.001,-2.2637内的误差大于4。
⑤在SM 2.x或者之后的硬件上，开发者可以指定--prec-sqrt=true，使误差降为0。

1. 转换为整型

根据C语言的运行时库的定义，函数nearbyint()和rint()会将浮点数按照当前方向取整到最接近的整型值，在CUDA中，会始终取整到最接近的偶数（round-to-nearst-even）。在C运行时中，nearbyint()和rint()的不同仅仅在处理INEXACT异常上。但是CUDA不会抛出浮点数的异常，2个函数的表现完全相同。

函数round()实现了最基本的取整策略：对处于相邻2个整数中间的浮点数，永远向上取整。英伟达公司反对使用这个函数，因为这个函数使用8条指令完成，而rint()函数和其变种仅仅使用1条。trunc()函数截断浮点值，向零取整，它会编译为1条指令。

2. 分数与指数

float frexpf(float x, int *eptr);

函数frexpf()会将输入的浮点数x分割为范围在[0.5,1.0]之间的浮点值Significand和以2为底的指数：

x=Significand  $\times 2$  Exponent
float logbf(float x);

函数logbf()取出x的指数并返回这个浮点数。除了它更快一点，它几乎等价于floorf(log2f(x))，如果x是非归一化，logbf()返回将x归一化后的指数值。

float ldexpf(float x, int exp); float scalbnf(float x, int n); float scanblnf(float x, long n);

函数ldexpf()、scalbnf()和scalblnf()都是通过在浮点指数上进行操作计算x2n的函数。

3. 浮点求余

函数modff()会分割输入的参数为小数和整数两部分。

float modff(float x, float *intpart);

返回值是x的小数部分，与x有着相同的符号。

函数remainderf(x,y)计算用x除以y的浮点余数。返回值为 x−n∗yx - n * y ，这里 nn 为 x/yx / y 并向最近的整数取整。如果 ∣x−n∗y∣=0.5|x - n * y| = 0.5 ， nn 会向偶数取整。

float remquof(float x, float y, int *quo);

计算余数，并将x/y整数商的低位返回，它与x/y有相同符号。

4. 贝塞尔函数

n阶贝塞尔函数与下述微分方程有关:

x2d2ydx2+xdydx+{x2−n2}y=0x ^ {2} \frac {d ^ {2} y}{d x ^ {2}} + x \frac {d y}{d x} + \left\{x ^ {2} - n ^ {2} \right\} y = 0

这里n可以为实数，但是为了与C运行时兼容，n被限定为非负整数。

解决二阶传统微分方程的方法结合了第一和第二类贝塞尔函数，如下所示：

y[x]=c1Jn[x]+c2Yn[x]y [ x ] = c _ {1} J _ {n} [ x ] + c _ {2} Y _ {n} [ x ]

数学函数 jn[f]()\mathrm{jn[f]()} 和 yn[f]()\mathrm{yn[f]()} 分别计算 Jn(x)\mathrm{J}_{\mathrm{n}}(\mathrm{x}) 和 Yn(x)\mathrm{Y}_{\mathrm{n}}(\mathrm{x}) 。j0f()、j1f()、y0f()和y1f()计算 n=0\mathrm{n} = 0 和 n=1\mathrm{n} = 1 情况下的函数值。

5.伽马函数

伽马函数是阶乘函数的扩展，对实数参数x，伽马函数对它减1。伽马函数的形式有许多种，其中的一种形式如下：

Γ[x]=∫0∞e−ttx−1dt\Gamma [ x ] = \int_ {0} ^ {\infty} e ^ {- t} t ^ {x - 1} d t

函数增长的非常快，以致即使使用相对较小输入值，其返回值也会超出精度，因此在函数tgamma()（“真实伽马函数”）之外，函数库提供了另一个函数lgamma()，返回伽马函数的自然对数。

8.3.7 延伸阅读

关于本节的专题，Goldberg的综述文章（标题很吸引人“whatever computer scientist should know about floating-point arithmetic”）是一个很好的介绍。

http://download.Oracle.com/docs/cd/E19957-01/806-3568/ncg_goldberg.html
英伟达公司的Nathan Whitehead和Alex Fit-Florea曾经共同撰写过白皮书：“Precision&Performance:Floating Point and IEEE 754 Compliance for NVIDIA GPUs.”。http://developer.download.nvidia.com/assets/cuda/files/NVIDIA-CUDAFloating-Point.pdf

增加有效精度

Dekker和Kahan研究了能提高浮点硬件有效精度几乎一倍的方法。他们用数对来换取指数范围的微小降低（源于中间数在区间两端的下溢和上溢）。阐述这一方法的论文包括：

Dekker, T.J. Point technique for extending the available precision. Numer. Math. 18, 1971, pp. 224 - 242.

Linnainmaa, S. Software for doubled-precision floating point computations. ACM TOMS 7, pp. 172 - 283 (1981).

Shewchuk, J.R. Adaptive precision floating-point arithmetic and fast robust geometric predicates. Discrete&Computational Geometry 18, 1997, pp. 305 - 363.

在该议题上，Andrew Thall、Da Graa和Defour做了一些直接与GPU相关的工作：

Guillaume, Da Graa, and David Defour. Implementation of float-float operators on graphics hardware, 7th Conference on Real Numbers and Computers, RNC7 (2006).

http://hal.archivesouvertes.fr/docs/00/06/33/56/PDF,float-float.pdf

Thall, Andrew. Extended-precision floating-point numbers for GPU computation. 2007.

http://andrewthall.org/papers/df64_qf128.pdf

[1] 有一例外，单精度非归一化浮点数在SM 1.x上根本不被支持。
[2] 有时也被称为次归一化。
[3] 事实上，GPU在具备完整的32位整型数支持之前就有完整的32位浮点支持。因此，一些早期的著作解释怎样用浮点硬件实现整型操作。
[4] Lindholm,Erik,John Nickolls,Stuart Oberman,and John Montrym.NVIDIA Tesla:A unified graphics and computing architecture.IEEE Micro,March-April 2008,p.47.
[5] half浮点值为纹理结构所支持，TEX指令会返回float型值，并且半浮点到浮点的转换是由纹理硬件自动执行的。

[6] 让每条指令编码取整模式和将其保存在控制寄存器中并不矛盾，Alpha处理器拥有一个2位编码来指定每一个指令的取整模式，其中一个设置是使用控制寄存器中指定的取整模式！CUDA硬件只使用了两个位编码来实现IEEE标准中的4种取整模式。

前の章8.2_整型支持
次の章8.4_条件代码
8.3_浮点支持 - CUDA专家手册 | OpenTech