14.1 概述

给定N个个体，个体i（1<N）的初始位置为x i，速度为v i，个体i受到来自个体j作用的力向量f ij 为：

f _ {j} = G \frac {m _ {i} m _ {j}}{\| d _ {j} \| ^ {2}} \cdot \frac {d _ {j}}{\| d _ {j} \|}

这里 $m_{i}$ 和 $m_{j}$ 分别表示个体 $i$ 和个体 $j$ 的质量； $d_{ij}$ 表示个体 $i$ 到个体 $j$ 的差向量； $G$ 是引力常数。由于除法可能导致溢出，表达式会因为 $d_{ij}$ 的幅值过小而发散。通常进行补偿的方法是使用一个软化因子，对两个普拉默质点（plummer mass）间的相互作用进行建模，普拉默质点把个体看成球形星体。假设软化因子为 $\varepsilon$ ，表达式将变成：

f _ {0} = G \frac {m _ {1} m _ {2} d _ {0}}{\left(\| d _ {0} \| ^ {2} + \varepsilon^ {2}\right) ^ {3 / 2}}

鉴于对i的影响来自其他N-1个个体，所有对个体i的作用为F $\mathbf{\mu}_{\mathrm{i}}$ ，是所有作用力的和：

\mathbf {F} _ {i} = \sum_ {j = 1} ^ {N} \mathbf {f} _ {i j} = G m _ {i} \sum_ {j = 1} ^ {N} \frac {m _ {i} m _ {j} \mathbf {d} _ {i j}}{\left(\left\| \mathbf {d} _ {i j} \right\| ^ {2} + \varepsilon^ {2}\right) ^ {3 / 2}}

原文公式中有笔误，已修正。——译者注

为了更新每个个体的位置和速度，对个体i产生的作用力（加速度）为 $a_{i} = F_{i} / m_{i}$ ，因此 $m_{i}$ 可以从表达式分子中删去，如下：

\mathbf {F} _ {i} = \sum_ {\substack {1 < j < N \\ j \neq i}} ^ {N} \mathbf {f} _ {i j} = G m _ {i} \sum_ {j = 1} ^ {N} \frac {m _ {j} \mathbf {d} _ {i j}}{\left(\| \mathbf {d} _ {i j} \| ^ {2} + \varepsilon^ {2}\right) ^ {3 / 2}}

就像Nyland等人一样，我们使用一个轮替跨越Verlet算法（整数步长的时间点），进行一个时间步长的模拟。个体的位置和速度值的改变是按照比对方增长半个时间步长方式进行，因为在我们的例子中，初始位置和速度是随机值，所以这一特点在代码中并不是十分的明显。我们的轮替Verlet方法先来更新速度，接下来更新位置：

\begin{array}{l} \mathbf {V} _ {i} \left(t + \frac {1}{2} \partial t\right) = \mathbf {V} _ {i} \left(t - \frac {1}{2} \partial t\right) + \partial t \mathbf {F} _ {i} \\ \mathbf {P} _ {i} (t + \partial t) = \mathbf {P} _ {i} (t) + \partial_ {t} \mathbf {V} _ {i} \left(t + \frac {1}{2} \partial t\right) \\ \end{array}

这种方式只是用于更新模拟系统的众多积分算法的一种，但是进一步的讨论已经超出本书的范畴。

因为积分运算的时间复杂度为O（N），而计算个体相互作用力的时间复杂度为O（N²），因此移植到CUDA平台的最大优势就是优化作用力计算的运行时间。优化这部分的计算时间也是本章的主要任务。

力的矩阵

一个实现N-体计算的简单算法，通过双重嵌套循环，计算每一个个体受到其他所有个体作用力的和。复杂度为 $O(N^{2})$ 的个体之间相互作用力的计算可以看作是一个NxN的矩阵，矩阵第i行的和是个体i的所有作用力的和：

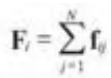
矩阵的对角线值为零，因为个体对自身作用力为零，因此可以忽略。

矩阵中的每一个元素是独立计算得到的，因此存在大量潜在的并行。每一行的和是一个归约，可以使用一个线程计算，也可以使用第12章中组合多个线程的结果进行计算。

图14-1考察了一个8-体矩阵。每一行的和对应的是计算的输出。当使用CUDA时，N-体计算通常使用一个线程来计算每一行的和。

因为矩阵中的每一个元素都是独立的，它们也可以在给定行中进行并行计算：例如计算每隔4个元素的和，然后将4个部分结果相加得到最终结果。Harris等人使用过这种方式，由于N较小以致没有足够的线程隐藏GPU的延时，他们的方法是这样的：启动更多的线程，在每个线程计算部分和，然后在共享内存上进行归约计算最终结果。Harris等人展示了当N<=4096时能够收到成效。

由于物理作用力是对称的（例如，个体i受到个体j的作用和个体j受到个体i作用是等大反向的），就像引力，矩阵的转置元素有相反的符号：

\textsf {f} _ {\textsf {i j}} = - \textsf {f} _ {\textsf {j i}}

在这种情况下，矩阵的形式如图14-2展示的那样。利用对称性，只需要计算矩阵右上三角的值，进行大约一半的计算。[1]

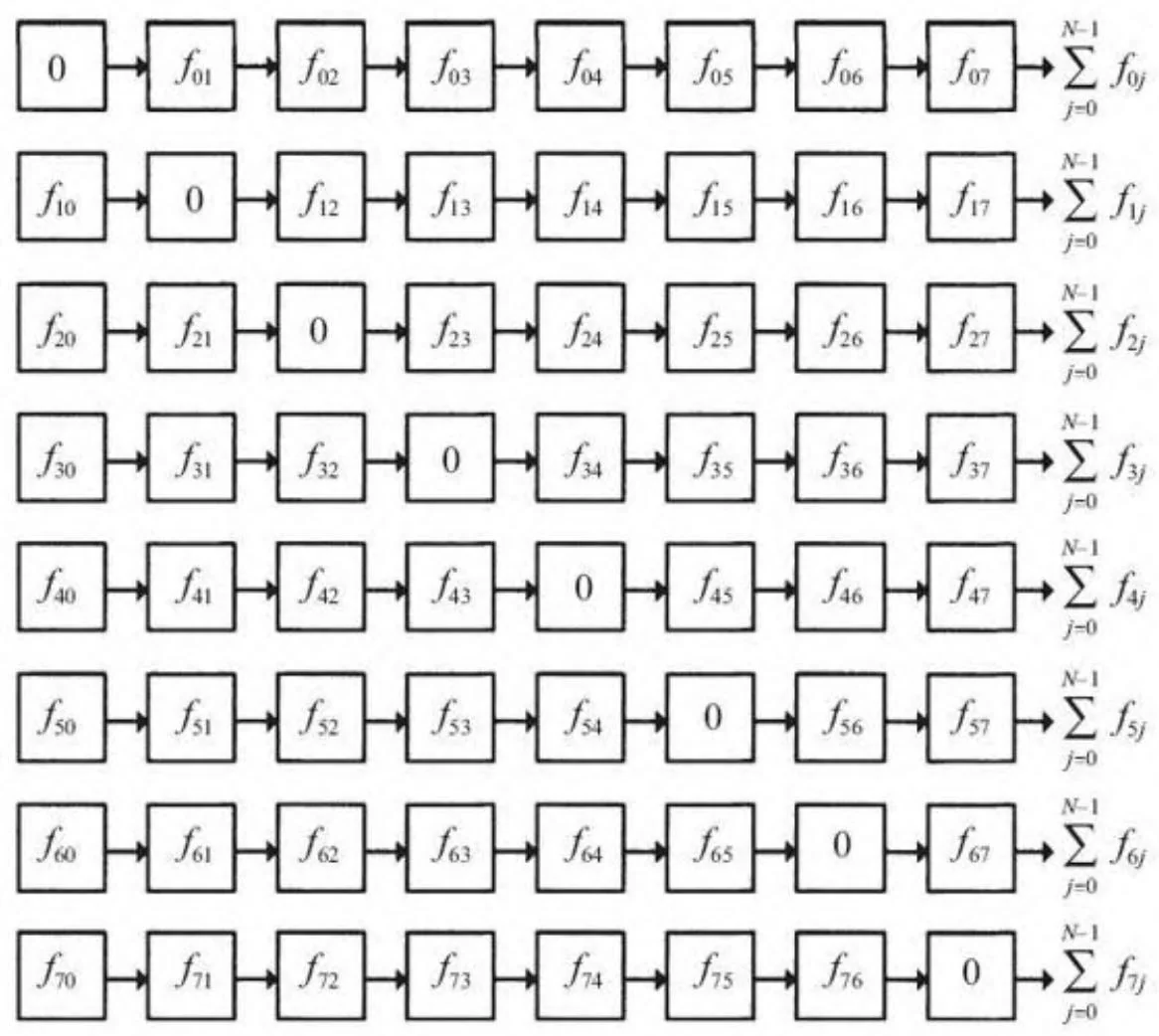
图14-1 作用力矩阵（8个体）

图14-2 作用力对称时的矩阵

现在的问题并不像图14-1那种暴力计算方法，当方法利用作用力的对称性时，不同的线程会对给定的输出和有所贡献。部分和不断被累计并保存到一个临时变量，最后进行归约计算，或者系统使用互斥机制来保护最终结果（使用原子操作或线程同步）。由于个体之间的计算量大约是20FLOPS（单精度）或者30FLOPS（双精度），减少总和的计算似乎对于性能的提升有着决定性作用。

不幸的是，多余的开销往往超过了仅执行一半计算带来的好处。例如，一个实现个体间计算中两个浮点数的原子加法比暴力计算方法更慢。

图14-3展示了一个对两种极端方法的折衷方案：通过对计算分块，只需要对右上角进行计算。对于一个尺寸为k的分块，这种方法需要在总数为 $\frac{N / k(N / k - 1)}{2}$ 的每个分块中进行k²次计算，然后再加上N/k个对角分块上分别进行k(k-1)个个体间计算。对于尺寸很大的N，个体间的计算节约时间大致相同，[2]但因为在尺寸为k的分块上可以进行部分和的计算并加到最终结果，可以降低同步带来的时间开销。图14-3展示了尺寸k=2的分块，但分块尺寸对应线程束（k=32）的大小是更实用的。

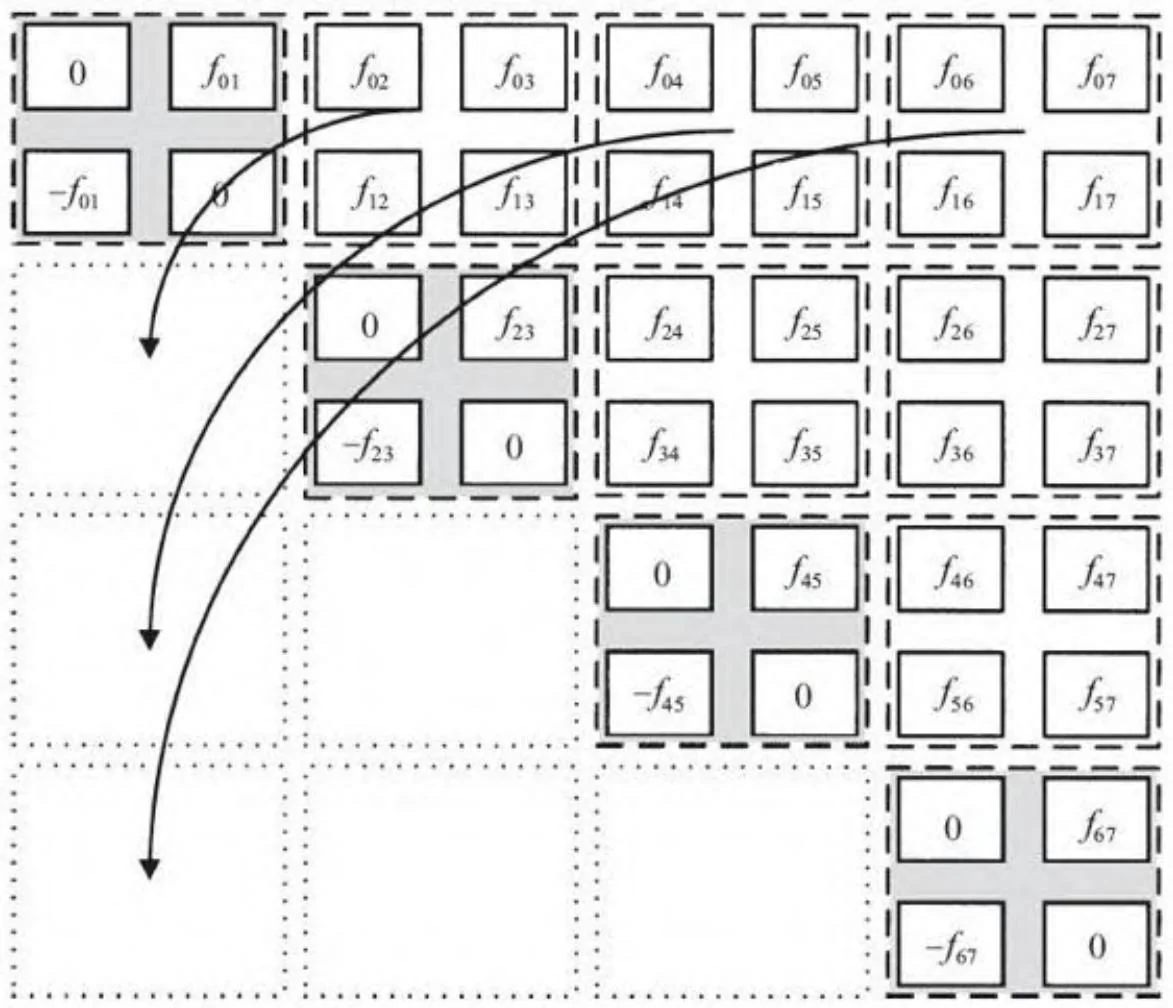
图14-3 分块的N-体问题 $(k = 2)$

图14-4展示了如何在给定的分块上进行部分和的计算。在行和列计算得到部分和（分别进行加和减），以得到必须被加到对应输出上的部分和。

流行于分子建模领域的“AMBER应用”利用了力的对称性，使用的分块大小调优后设置为线程束的大小32，[3]但是在大量的测试中，这种方法并未在此处描述的轻量级计算中显现出优势。

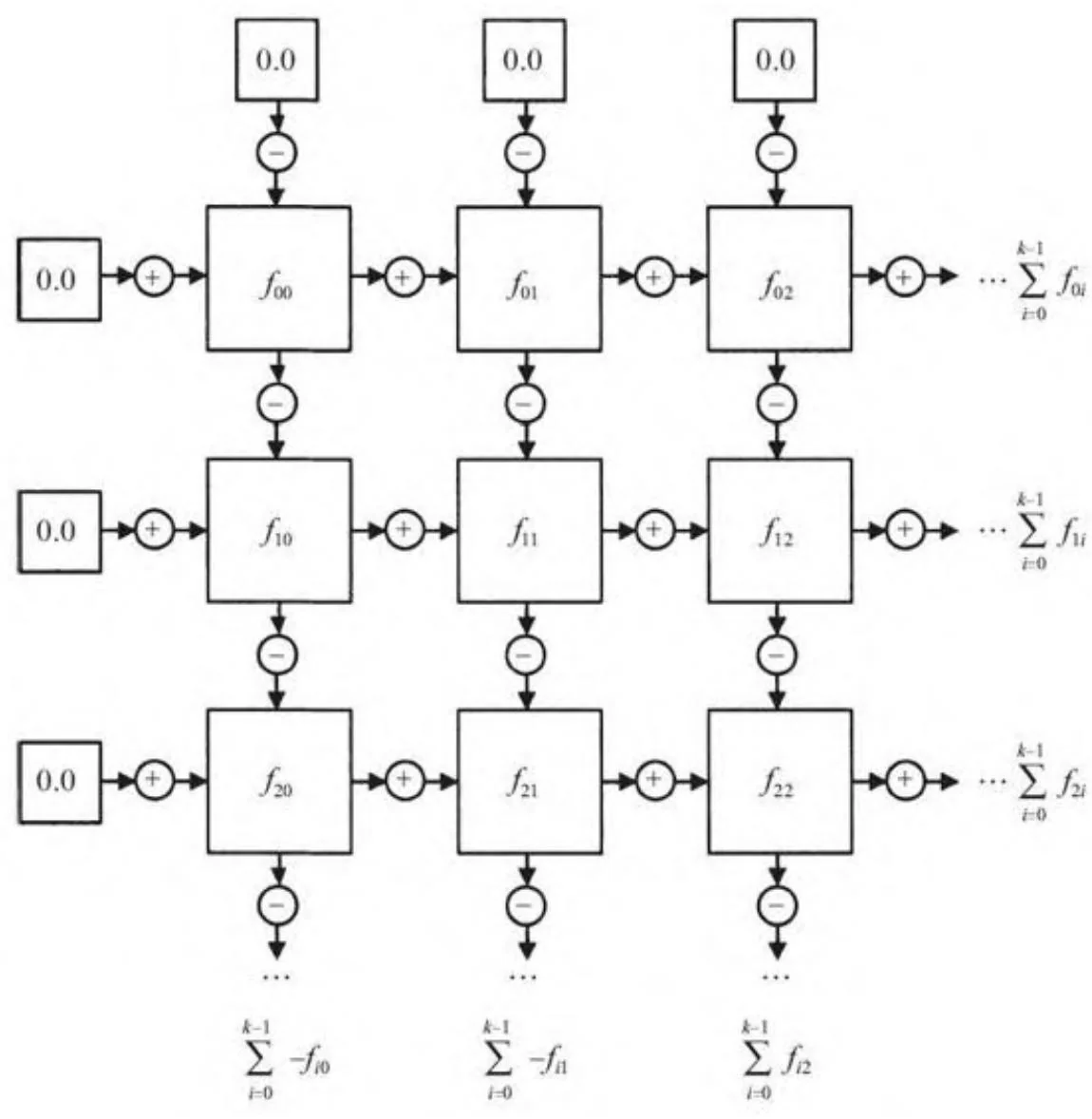
图14-4 N-体的一个分块

[1] 准确来说，要计算N（N-1）/2个作用力。
[2] 例如，使用 $\mathrm{N} = 65536$ 和 $\mathrm{k} = 32$ ，这种方法仅是暴力计算 $52.5\%$ 的性能，虽然相对于对称算法提高了 $3\%$ 的性能。
[3] Gótz, Andreas, Mark J. Williamson, Dong Xu, Duncan Poole, Scott Le Grand, and Ross C. Walker. Routine microsecond molecular dynamics

simulations with AMBER on GPUs—Part I: Generalized Born, J. Chem. Theory Comput. 8, no.5 (2012), pp.1542-1555.

14.1_概述

14.1 概述

力的矩阵