假设车间生产了一批螺丝,你想检验这些产品质量情况,你随机抽查了一些螺丝,此时就可以使用统计抽样的四大分布是:正态分布、卡方分布、t分布和F分布,他们分别对应 Z检验、卡方检验、t检验和F检验。 如果你抽查的样本比较多(n>30)优先使用Z检验 (对应正态分布 ),如果抽查样本比较少(n<20)则使用t检验 (对应t分布 ),如果你想比较两个机床生产的螺丝质量差异则使用F检验 (对应F分布 )。如果想分析螺丝质量和原材料质量的关系则使用χ²卡方检验 (对应卡方分布 )
χ²分布、t分布、F分布的主要用途,其实不是拿来用于自然现象的建模,而是用于假设检验用的。只有正态分布既可以进行建模又可以进行检验
F分布的引入-F检验 假设你是公司的老板,有两台机床加工同种零件,有一天,你分别从车床A A A B B B 6 6 6 9 9 9 s 1 2 = 0.345 s_1^2=0.345 s 1 2 = 0.345 s 2 2 = 0.375 s_2^2=0.375 s 2 2 = 0.375 A A A B B B 9 9 9 9 9 9 A A A B B B B B B A A A A A A B B B
对于这个问题,我们先给出解答,详细的可以在后面章节理解。
解 设两总体 X X X Y Y Y N ( μ 1 , σ 1 2 ) N\left(\mu_1, \sigma_1^2\right) N ( μ 1 , σ 1 2 ) N ( μ 2 , σ 2 2 ) , μ 1 , μ 2 , σ 1 2 , σ 2 2 N\left(\mu_2, \sigma_2^2\right), \mu_1, ~ \mu_2, ~ \sigma_1^2, ~ \sigma_2^2 N ( μ 2 , σ 2 2 ) , μ 1 , μ 2 , σ 1 2 , σ 2 2 H 0 : σ 1 2 = σ 2 2 , H 1 : σ 1 2 ≠ σ 2 2 H_0: \sigma_1^2=\sigma_2^2, ~ H_1: \sigma_1^2 \neq \sigma_2^2 H 0 : σ 1 2 = σ 2 2 , H 1 : σ 1 2 = σ 2 2 F = S 1 2 / S 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) F=S_1^2 / S_2^2 \sim F\left(n_1-1, n_2-1\right) F = S 1 2 / S 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) α \alpha α k 1 , k 2 k_1, ~ k_2 k 1 , k 2 P { F < k 1 P\left\{F<k_1\right. P { F < k 1 F > k 2 } = α \left.F>k_2\right\}=\alpha F > k 2 } = α
k 1 = F 1 − α / 2 ( n 1 − 1 , n 2 − 1 ) = F 0.95 ( 5 , 8 ) = 1 F 0.05 ( 8 , 5 ) = 0.208 , k 2 = F α / 2 ( n 1 − 1 , n 2 − 1 ) = F 0.05 ( 5 , 8 ) = 3.69 , \begin{gathered}
k_1=F_{1-\alpha / 2}\left(n_1-1, n_2-1\right)=F_{0.95}(5,8)=\frac{1}{F_{0.05}(8,5)}=0.208, \\
k_2=F_{\alpha / 2}\left(n_1-1, n_2-1\right)=F_{0.05}(5,8)=3.69,
\end{gathered} k 1 = F 1 − α /2 ( n 1 − 1 , n 2 − 1 ) = F 0.95 ( 5 , 8 ) = F 0.05 ( 8 , 5 ) 1 = 0.208 , k 2 = F α /2 ( n 1 − 1 , n 2 − 1 ) = F 0.05 ( 5 , 8 ) = 3.69 , 从而拒绝域为 F < 0.208 F<0.208 F < 0.208 F > 3.69 F>3.69 F > 3.69 s 1 2 = 0.345 , s 2 2 = 0.375 s_1^2=0.345, s_2^2=0.375 s 1 2 = 0.345 , s 2 2 = 0.375 F = s 1 2 / s 2 2 = 0.92 F=s_1^2 / s_2^2=0.92 F = s 1 2 / s 2 2 = 0.92 0.208 < 0.92 < 3.69 0.208<0.92<3.69 0.208 < 0.92 < 3.69 H 0 H_0 H 0
这就是F分布在方差分析里的实际作用的一个实例
F分布广泛应用在方差分析 、回归分析显著性检验 以及两正态总体方差比 的推断里
F分布的定义 定义 :设随机变量 X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X \sim \chi^2(m), Y \sim \chi^2(n) X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X X X Y Y Y F = X / m Y / n F = \frac{X / m}{Y / n} F = Y / n X / m m m m n n n F ∼ F ( m , n ) F \sim \mathrm{F}(m, n) F ∼ F ( m , n )
F分布通常定义为:两个独立的卡方分布随机变量各自除以其自由度后的比值所服从的分布。
F分布是由英国统计学家罗纳德·艾尔默·费舍尔(Ronald Aylmer Fisher)于1924年首次提出并系统阐述的。所以这一分布以他姓氏的首字母“F”命名,以表彰其开创性贡献。美国统计学家乔治·W·斯内德科尔(George W. Snedecor)在后续推广和应用中也发挥了关键作用,因此该分布有时也被称为Fisher-Snedecor分布
咦,有没有感觉奇怪?F分布没有密度函数,为什么? 因为表达式太长了,基本上没有存在的意义,就这么着吧,直接使用定义。这也说明,密度函数(比如指数分布,伽玛分布,正态分布)都看起来非常吓人,其实,那都是数学家拟合出来的,没有密度函数,照样可以建模。
F分布用于检验方差是否不同,本质用于分析两个方差是否相等的问题。它的构造是基于正态分布的样本方差的比值来定义的。具体来说,假设有两个样本x 1 , x 2 , . . . x m x_1,x_2,...x_m x 1 , x 2 , ... x m y 1 , y 2 , . . . . y n y_1,y_2,....y_n y 1 , y 2 , .... y n x i {x_i} x i y i {y_i} y i s 2 x s^2x s 2 x s 2 y s^2y s 2 y F = s 2 x s 2 y F=\frac{s^2x}{s^2y} F = s 2 y s 2 x F F F F F F m m m n n n
F F F F F F
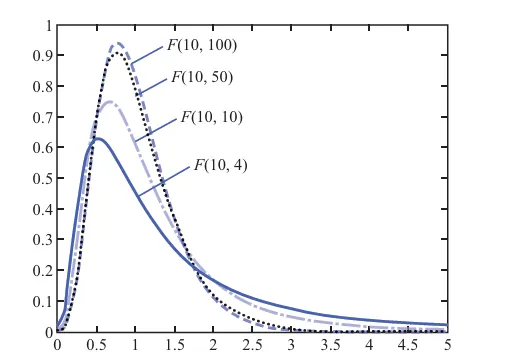
不同自由度的F分布图
F分位数 设 X ∼ F ( m , n ) X \sim F(m, n) X ∼ F ( m , n ) α \alpha α F α ( m , n ) F_\alpha(m, n) F α ( m , n ) F α ( m , n ) F_\alpha(m, n) F α ( m , n )
P ( X ≤ F α ( m , n ) ) = α .
P\left(X \leq F_\alpha(m, n)\right)=\alpha \text {. }
P ( X ≤ F α ( m , n ) ) = α . 根据 F F F
F α ( m , n ) = 1 F 1 − α ( n , m ) . \boxed{
F_\alpha(m, n)=\frac{1}{F_{1-\alpha}(n, m)} .
} F α ( m , n ) = F 1 − α ( n , m ) 1 . 证明:设 F ∼ F ( m , n ) F \sim F(m, n) F ∼ F ( m , n ) F = X / m Y / n F {=} \frac{X / m}{Y / n} F = Y / n X / m X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X \sim \chi^2(m), Y \sim \chi^2(n) X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X X X Y Y Y 1 F = Y / n X / m ∼ F ( n , m ) \frac{1}{F} {=} \frac{Y / n}{X / m} \sim F(n, m) F 1 = X / m Y / n ∼ F ( n , m ) P ( F ≤ F α ( m , n ) ) = P ( 1 F ≥ 1 F α ( m , n ) ) = α P\left(F \leq F_\alpha(m, n)\right)=P\left(\frac{1}{F} \geq \frac{1}{F_\alpha(m, n)}\right)=\alpha \quad P ( F ≤ F α ( m , n ) ) = P ( F 1 ≥ F α ( m , n ) 1 ) = α P ( 1 F ≤ 1 F α ( m , n ) ) = 1 − α P\left(\frac{1}{F} \leq \frac{1}{F_\alpha(m, n)}\right)=1-\alpha P ( F 1 ≤ F α ( m , n ) 1 ) = 1 − α 1 F ∼ F ( n , m ) \frac{1}{F} \sim F(n, m) F 1 ∼ F ( n , m )
1 F α ( m , n ) = F 1 − α ( n , m ) \frac{1}{F_\alpha(m, n)}=F_{1-\alpha}(n, m) F α ( m , n ) 1 = F 1 − α ( n , m ) 例题 例 设随机变量 X 1 , X 2 , ⋯ , X 5 X_1, X_2, \cdots, X_5 X 1 , X 2 , ⋯ , X 5 X i ∼ N ( 0 , 1 ) , i = 1 , ⋯ , 5 X_i \sim N(0,1), i=1, \cdots, 5 X i ∼ N ( 0 , 1 ) , i = 1 , ⋯ , 5 a a a
a X 1 2 + X 2 2 X 3 2 + X 4 2 + X 5 2 a \frac{X_1^2+X_2^2}{X_3^2+X_4^2+X_5^2} a X 3 2 + X 4 2 + X 5 2 X 1 2 + X 2 2 服从 F F F X i ∼ N ( 0 , 1 ) , i = 1 , 2 , ⋯ , 5 X_i \sim N(0,1), i=1,2, \cdots, 5 X i ∼ N ( 0 , 1 ) , i = 1 , 2 , ⋯ , 5
X 1 2 + X 2 2 ∼ χ 2 ( 2 ) , X 3 2 + X 4 2 + X 5 2 ∼ χ 2 ( 3 ) X_1^2+X_2^2 \sim \chi^2(2), X_3^2+X_4^2+X_5^2 \sim \chi^2(3) X 1 2 + X 2 2 ∼ χ 2 ( 2 ) , X 3 2 + X 4 2 + X 5 2 ∼ χ 2 ( 3 ) 且两者相互独立,由定义知
( X 1 2 + X 2 2 ) / 2 ( X 3 2 + X 4 2 + X 5 2 ) / 3 ∼ F ( 2 , 3 ) 所以,取 a = 3 2 即可,且自由度为 2 和 3. \begin{aligned}
&\frac{\left(X_1^2+X_2^2\right) / 2}{\left(X_3^2+X_4^2+X_5^2\right) / 3} \sim F(2,3)\\
&\text { 所以,取 } a=\frac{3}{2} \text { 即可,且自由度为 } 2 \text { 和 } 3 .
\end{aligned} ( X 3 2 + X 4 2 + X 5 2 ) /3 ( X 1 2 + X 2 2 ) /2 ∼ F ( 2 , 3 ) 所以,取 a = 2 3 即可,且自由度为 2 和 3. 例设随机变量 T ∼ t ( n ) T \sim t(n) T ∼ t ( n ) F = 1 T 2 F=\frac{1}{T^2} F = T 2 1
解:由于 T ∼ t ( n ) T \sim t(n) T ∼ t ( n ) T = X Y / n T=\frac{X}{\sqrt{Y / n}} T = Y / n X X X X Y Y Y X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X \sim N(0,1), Y \sim \chi^2(n) X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n )
则 F = 1 T 2 = Y / n X 2 F=\frac{1}{T^2}=\frac{Y / n}{X^2} F = T 2 1 = X 2 Y / n X 2 ∼ χ 2 ( 1 ) X^2 \sim \chi^2(1) X 2 ∼ χ 2 ( 1 ) X 2 X^2 X 2 Y Y Y F F F F ∼ F ( n , 1 ) F \sim F(n, 1) F ∼ F ( n , 1 )
由F定义可知,若 X 1 , X 2 , X 3 X_1, X_2, X_3 X 1 , X 2 , X 3 N ( 0 , 1 ) N(0,1) N ( 0 , 1 ) X 1 2 ∼ χ 2 ( 1 ) , X 2 2 + X 3 2 ∼ χ 2 ( 2 ) \quad X_1^2 \sim \chi^2(1), X_2^2+X_3^2 \sim \chi^2(2) X 1 2 ∼ χ 2 ( 1 ) , X 2 2 + X 3 2 ∼ χ 2 ( 2 ) X 1 2 X_1^2 X 1 2 X 2 2 + X 3 2 X_2^2+X_3^2 X 2 2 + X 3 2
X 1 2 / 1 ( X 2 2 + X 3 2 ) / 2 = 2 X 1 2 X 2 2 + X 3 2 = ( 2 X 1 X 2 2 + X 3 2 ) 2 ∼ F ( 1 , 2 ) . \frac{X_1^2 / 1}{\left(X_2^2+X_3^2\right) / 2}=\frac{2 X_1^2}{X_2^2+X_3^2}=\left(\frac{\sqrt{2} X_1}{\sqrt{X_2^2+X_3^2}}\right)^2 \sim F(1,2) . ( X 2 2 + X 3 2 ) /2 X 1 2 /1 = X 2 2 + X 3 2 2 X 1 2 = ( X 2 2 + X 3 2 2 X 1 ) 2 ∼ F ( 1 , 2 ) . 例 设 X 1 , X 2 , ⋯ , X 15 X_1, X_2, \cdots, X_{15} X 1 , X 2 , ⋯ , X 15 N ( 0 , 2 2 ) N\left(0,2^2\right) N ( 0 , 2 2 ) Y = X 1 2 + X 2 2 + ⋯ + X 10 2 2 ( X 11 2 + X 12 2 + ⋯ + X 15 2 ) Y=\frac{X_1^2+X_2^2+\cdots+X_{10}^2}{2\left(X_{11}^2+X_{12}^2+\cdots+X_{15}^2\right)} Y = 2 ( X 11 2 + X 12 2 + ⋯ + X 15 2 ) X 1 2 + X 2 2 + ⋯ + X 10 2
解 由 X i ∼ N ( 0 , 2 2 ) X_i \sim N\left(0,2^2\right) X i ∼ N ( 0 , 2 2 ) X i 2 ∼ N ( 0 , 1 ) ( i = 1 , 2 , ⋯ , 15 ) \frac{X_i}{2} \sim N(0,1)(i=1,2, \cdots, 15) 2 X i ∼ N ( 0 , 1 ) ( i = 1 , 2 , ⋯ , 15 ) χ 2 \chi^2 χ 2
X 1 2 + X 2 2 + ⋯ + X 10 2 2 2 ∼ χ 2 ( 10 ) , X 11 2 + X 12 2 + ⋯ + X 15 2 2 2 ∼ χ 2 ( 5 ) . \begin{aligned}
& \frac{X_1^2+X_2^2+\cdots+X_{10}^2}{2^2} \sim \chi^2(10), \\
& \frac{X_{11}^2+X_{12}^2+\cdots+X_{15}^2}{2^2} \sim \chi^2(5) .
\end{aligned} 2 2 X 1 2 + X 2 2 + ⋯ + X 10 2 ∼ χ 2 ( 10 ) , 2 2 X 11 2 + X 12 2 + ⋯ + X 15 2 ∼ χ 2 ( 5 ) . 进而有
Y = X 1 2 + X 2 2 + ⋯ + X 10 2 2 ( X 11 2 + X 12 2 + ⋯ + X 15 2 ) = X 1 2 + X 2 2 + ⋯ + X 10 2 2 2 ÷ 10 X 11 2 + X 12 2 + ⋯ + X 15 2 2 2 ÷ 5 ∼ F ( 10 , 5 ) \begin{aligned}
Y & =\frac{X_1^2+X_2^2+\cdots+X_{10}^2}{2\left(X_{11}^2+X_{12}^2+\cdots+X_{15}^2\right)} \\
& =\frac{\frac{X_1^2+X_2^2+\cdots+X_{10}^2}{2^2} \div 10}{\frac{X_{11}^2+X_{12}^2+\cdots+X_{15}^2}{2^2} \div 5} \sim F(10,5)
\end{aligned} Y = 2 ( X 11 2 + X 12 2 + ⋯ + X 15 2 ) X 1 2 + X 2 2 + ⋯ + X 10 2 = 2 2 X 11 2 + X 12 2 + ⋯ + X 15 2 ÷ 5 2 2 X 1 2 + X 2 2 + ⋯ + X 10 2 ÷ 10 ∼ F ( 10 , 5 ) {width=500px}