14._卡方分布χ²-前世今生-Part5
如《深入理解χ2分布》的几个例子,χ2值的计算很简单,就是用(观测值频数-理论值频数)^2之后,除以理论值频数,然后再求和Σ,就计算出来了。
我们现在很多统计应用的书籍中,关于χ2值的计算都是这样。
那到底χ2是如何与观测值频数与理论值的频数相扯上关系的?
此时我们回到《深入理解χ2分布(上)》文中最初的式子。
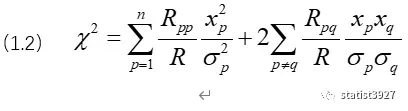
它是χ2值一般的形式。
在这里插一嘴:
其实刚看到(1.2)式的时候,我总觉得好像哪里见过
比方说有点儿像中学学的和平方公式
只不过上式套一个Σ而已
或者说已故的经济学诺奖得主 哈利·马克思·马科维茨(Harry Max Markowitz),他的经典资产组合理论中有这么一条关于投资组合的方差表达式:
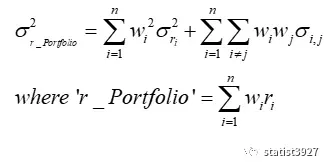
上式中,w代表每种资产的配置权重,r代表不同的资产收益率。
也正因为看着比较眼熟,所以才激发了我持续对这个经典理论的微考古的兴趣和动力。
下面言归正传
要对一般形式进行计算得到χ2值,这里面有几个元素就必须要计算出来。
它们分别是:行列式R,余子式Rpp和Rpq,以及σp,σq
下面就是关于它们的计算。
如果有N次的观测值,分了n个组,那么就会有n个观测频数 m1’,m2’……mn’,同时也存在n个理论频数m1,m2……mn,
令e=m’-m,那么就会有n个观测和理论差异产生的误差,e1,e2,……en。
I. 令p∈{n},ep的标准差由二项式分布的方差开方得
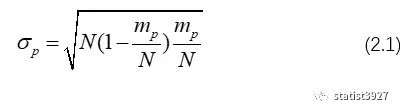
II. 如果rpq是ep和eq的相关系数,那么根据2组变量的相关系数
rpq=cov (p,q)/σpσq,得:
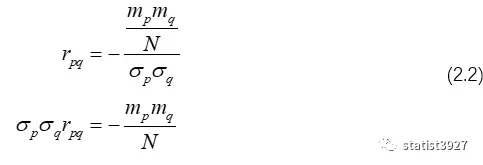
在这里Pearson给相关系数加了个负号。
III. 引入一个辅助角β,构建ep的概率为mq/N=sin2βq,代入(2.1)于是可以得到

(2.3)代入到(2.2),得到

因此,(1.2)式中的R,也就是相关系数矩阵行列式,把(2.4)式代入后,可以表示为
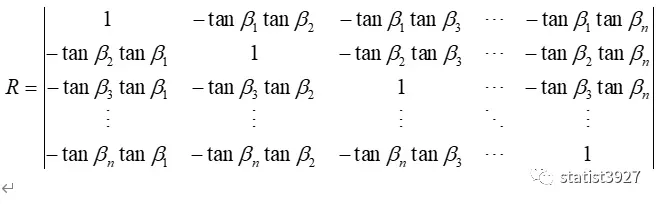
接下来进行的推导和简化R:
这里Pearson没有显性化他的推导过程,直接就给了结论。我在此补充下
第1列提取公因子-tanβ1,第2列提取公因子-tanβ2,第3列提取公因子-tanβ3
依此类推,会得到过渡行列式的公因式(-1)ntanβ1tanβ2tanβ3…tanβn
接下来,再在这个过渡行列式中,
第1行提取公因子tanβ1,第2行提取公因子tanβ2,第3行提取公因子tanβ3.....依次类推,
最后会得到R的公因子式:(-1)ntan2β1tan2β2tan2β3…tan2βn,于是整个行列式R就会变型成如下:

基于这种变换,上式中蓝色部分,可以用于表示(1.2)式中Rpq代表的余子式,并依次类推。
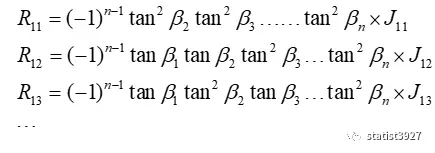
那么问题又来了,如何去简化计算这个R和它的这些余子式呢?
IV. 此时,根据III. 中的mq/N=sin2βq构建

那么,在III.中的蓝色部分式子中的J,将(2.5)代入,就可以表示成

J的代数余子式,例如J12,根据代数余子式定义可以表示成
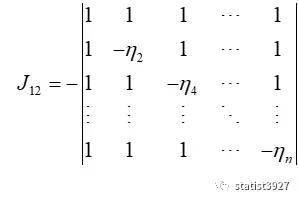
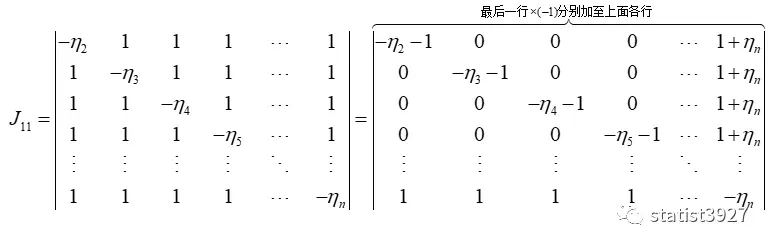
此时,用第1行×(-1)与第2行相加,第1行×(-1)与第3行相加……,一直加到最后一行,就构成了个一个上三角行列式,就很容易求得到J12的值
J12=(-1)n-1(η3+1) (η4+1)……(ηn+1)
特别的,令
λ=(η1+1) (η2+1) (η3+1)……(ηn+1),
那么就有
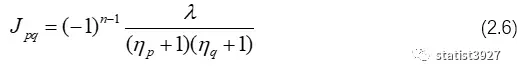
注意,此时必须是p≠q,因为以J11为例,就不是(2.6)能够表示的。
所以,必须补齐J11场景下的表达式。
在这里,我没有用Pearson原文的过程
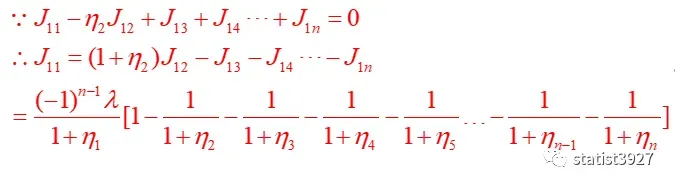
主要是这个过程从第一步开始,我思考了很久,也检索了很多线性代数的知识,还是没找到背后的原理。
于是我直接通过行列式的代数余子式外加基本的行列式计算规则,也得到了这个相同的结果。
不过这个J11的推导过程很考验读者的线性代数基本功底。
我是用了1页多A4纸才完整的推导出来。
由于中间过程要很仔细,因此我没有拿笔算,而是用公式编辑器来推导。
用公式编辑器推导的好处,就是一旦发现有错可以立刻原地修改,里面的元素位置对正、行列调整等等的操作很规范,非常容易检查。
我把J11的推导过程放到了本文的最后部分,有兴趣的读者可以自行阅读。
在这里得到:
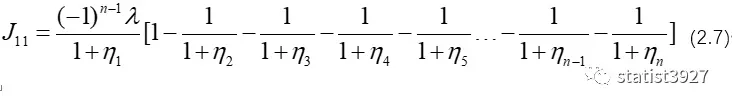
也非常感谢自己,趟了一次完整的(2.7)推导,我能够比较轻松地通过这个推导过程,得到J的值
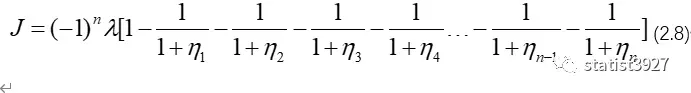
于是设定n∈{N},可以通过(2.5)得到

将上面的过程代入到(2.8),得到
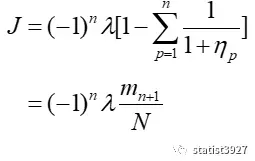
类似的,将之代入到(2.7) 以及其他主对角线元素的Jpp也会得到
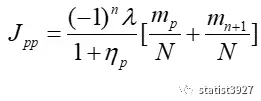
知道了J和Jpp后,回代入由之前的
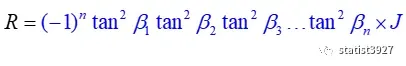
和Rpq代表的余子式
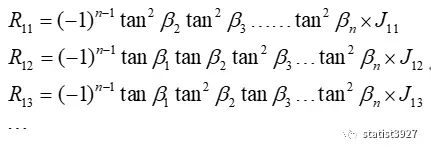 得到:
得到:
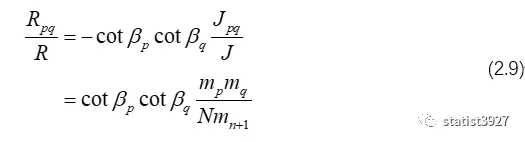
以及

将(2.9)和(2.10)最终跨过太平洋代回到最早的(1.2)式
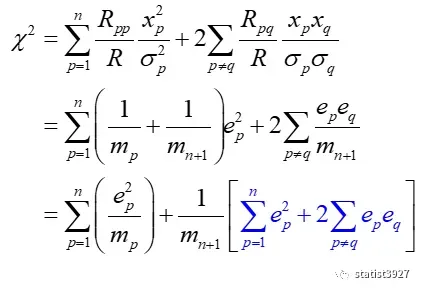
在这里,又出现一个隐藏的,不容易让人看懂的一点,就是上面式子最后一步中的蓝色部分
巧妙之处在哪里呢?
I: p和q都在[1,n]中,由于p≠q,它们分别对不同的观测误差e进行标识;
II: ΣΣepeq代表了n个观测误差e中,任意2个不同的观测误差相乘,然后求和
III: 这样,上式的蓝色部分刚好就是n个ep之和的平方展开,也就是
(ep1+ep2+ep3……+epn)2,尽管里面没有q再出现了。
这样上式就会变化成这样
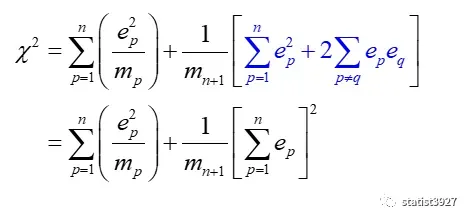
此时要处理掉mn+1项,于是请出上一文章就讲到的自由度的概念:
因为Σen+en+1=0→Σen=-en+1
因此得到了终极答案:

(2.11)也就是我们经常在教科书里介绍的那个公式
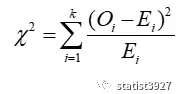
最后回顾
I: 卡方χ2值,无论是一般场景还是独立同标准正态分布,都可以由
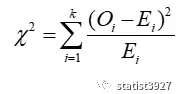
进行计算
II: 如果总的分组n是奇数,n去掉自由度后为偶数,那么P值的计算为
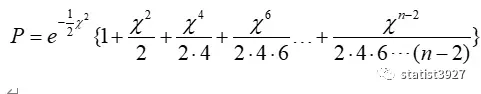
III: 如果n总的分组是偶数,n去掉自由度后为奇数,那么P值的计算
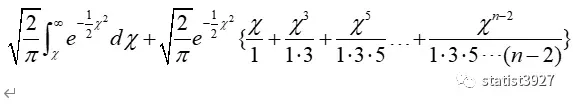
附:J11的推导过程
本文摘自微信公众号,点击 https://mp.weixin.qq.com/s/acr1Jm8Y0iJkkaib2V6MIw 查看原文