假设车间生产了一批螺丝,你想检验这些产品质量情况,你随机抽查了一些螺丝,此时就可以使用统计抽样的四大分布是:正态分布、卡方分布、t分布和F分布,他们分别对应 Z检验、卡方检验、t检验和F检验。 如果你抽查的样本比较多(n>30)优先使用Z检验 (对应正态分布 ),如果抽查样本比较少(n<20)则使用t检验 (对应t分布 ),如果你想比较两个机床生产的螺丝质量差异则使用F检验 (对应F分布 )。如果像分析螺丝质量和原材料质量的关系则使用χ²卡方检验 (对应卡方分布 )
χ²分布、t分布、F分布的主要用途,其实不是拿来用于自然现象的建模,而是用于假设检验用的。只有正态分布既可以进行建模又可以进行检验
引入 ①假设你是一个初中中学的校长,有一天,你希望了解一下全校初一年级学生的平均身高,学校初一年级共10个班级,为了减少干扰,你随机找了三个初一班级的班主任,记做X 1 , X 2 , X 3 X_1,X_2,X_3 X 1 , X 2 , X 3 X 1 = { x ∣ 1.65 , 1.68 , 1.7 , 1.6 , 1.58 , 1.66 , 1.66 , 1.67 , 1.69 , 1.65 } X_1=\{x|1.65,1.68,1.7,1.6,1.58,1.66,1.66,1.67,1.69,1.65 \} X 1 = { x ∣1.65 , 1.68 , 1.7 , 1.6 , 1.58 , 1.66 , 1.66 , 1.67 , 1.69 , 1.65 } X 2 = { x ∣ 1.75 , 1.72 , 1.54 , 1.60 , 1.66 , 1.66 , 1.66 , 1.67 , 1.68 , 1.65 } X_2=\{x|1.75,1.72,1.54,1.60,1.66,1.66,1.66,1.67,1.68,1.65 \} X 2 = { x ∣1.75 , 1.72 , 1.54 , 1.60 , 1.66 , 1.66 , 1.66 , 1.67 , 1.68 , 1.65 } X 3 = { x ∣ 1.6 , 1.61 , 1.7 , 1.66 , 1.64 , 1.65 , 1.66 , 1.67 , 1.68 , 1.9 } X_3=\{x|1.6,1.61,1.7,1.66,1.64,1.65,1.66,1.67,1.68,1.9 \} X 3 = { x ∣1.6 , 1.61 , 1.7 , 1.66 , 1.64 , 1.65 , 1.66 , 1.67 , 1.68 , 1.9 } Y = X 1 2 + X 2 2 + X 3 2 Y=X_1^2+X_2^2+X_3^2 Y = X 1 2 + X 2 2 + X 3 2
②想象你在玩掷骰子的游戏,每掷一次就记录下来点数。如果你掷了很多次,比如几百甚至几千次,你可能会好奇:我得到的这些点数分布,是否真的是公平的?即每个点数出现的概率都是相同的?卡方分布就是用来回答这类问题的一个工具。它能帮助我们检验观察到的数据与预期数据之间是否有显著差异。例如你有一个骰子,掷了 600 次,想检验它是否是公平的。理论上,每个面出现的次数应该是 100 次,实际观察到的次数可能是 [ 95 , 105 , 93 , 107 , 100 , 100 ] [95,105,93,107,100,100] [ 95 , 105 , 93 , 107 , 100 , 100 ]
以特定概率 分布为某种情况在进行数学建模时,事物长期结果较为稳定,能够清晰进行把握。但是期望与事实存在差异怎么办?偏差是正常的小幅度波动?还是建模错误?此时,利用卡方分布分析结果,排除可疑结果。【事实与期望不符合情况下使用卡方分布进行检验】
比如:抽奖机,肯定都不陌生,现在一些商场超市门口都有放置。正常情况下出奖概率是一定的,基本商家收益。倘若突然某段时间内总是出奖,甚是反常,那么到底是某阶段是小概率事件还是有人进行操作了?抽奖机怎么了?针对这种现象或者类似这种现象问题则可以借助卡方进行检验,具体如何检验后面会介绍。这里说明一下基础知识。
这里为什么要使用X 2 X^2 X 2
在上节里,得到一个重要公式
∑ ( 观察值 − 预期值 ) 2 预期值 {
\sum \dfrac{(\text { 观察值 }- \text { 预期值 })^2}{\text { 预期值 }}
} ∑ 预期值 ( 观察值 − 预期值 ) 2 现在我们对上面公式进行抽象,改写为
χ c 2 = ∑ ( O i − E i ) 2 E i \boxed{
\chi_c^2=\sum \frac{\left(O_i-E_i\right)^2}{E_i}
} χ c 2 = ∑ E i ( O i − E i ) 2 用于卡方检验的卡方统计量。 c:自由度。O:观测值。E:期望值。
这个等式是什么意思?为什么这个公式是卡方检验的检验统计量?
提示:检验统计量看起来类似于方差公式 ∑ ( x i − μ ) 2 / n \sum\left(x_i-\mu\right)^2 / n ∑ ( x i − μ ) 2 / n
卡方检验统计量基本上是观察值与期望值之间标准化的平方差之和。之所以说它是标准化的,是因为它将平方差除以预期值,就像任何典型的标准化一样。基本上,这个检验统计量可以告诉你观测值与预期值的偏差有多大。
χ 2 \chi^2 χ 2 定义 设 X 1 , ⋯ , X n X_1, \cdots, X_n X 1 , ⋯ , X n N ( 0 , 1 ) N(0,1) N ( 0 , 1 ) Y = X 1 1 + X 2 2 + . . . + X n 2 = ∑ i = 1 n X i 2 Y = X_1^1+X_2^2+...+X_n^2=\sum_{i=1}^n X_i^2 Y = X 1 1 + X 2 2 + ... + X n 2 = ∑ i = 1 n X i 2 n n n χ 2 \chi^2 χ 2 Y ∼ χ 2 ( n ) Y \sim \chi^2(n) Y ∼ χ 2 ( n )
(1)n = 1 n=1 n = 1 n = 2 n=2 n = 2 n = 3 , 4 , 5... n=3,4,5... n = 3 , 4 , 5... n n n
自由度是指上式右端所包含的独立变量的个数
χ 2 \chi^2 χ 2 整体 ,从定义可以看到他是X 2 X^2 X 2 量纲 ”一致,所以用的是χ 2 \chi^2 χ 2 χ ∗ χ \chi * \chi χ ∗ χ
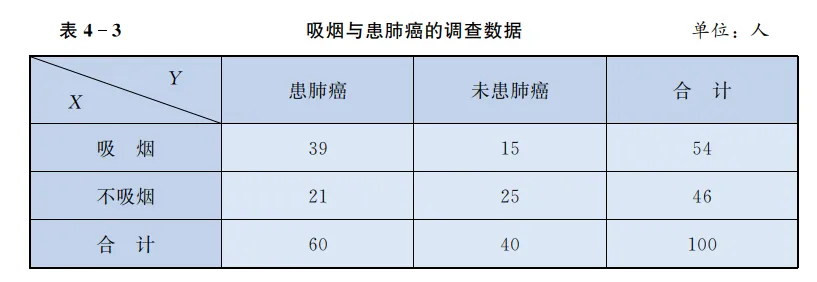
卡方χ 2 \chi^2 χ 2 借助上一节“吸烟与肺癌 ”的例子
我们看上面卡方的定义,当 X i X_i X i X 2 X^2 X 2
X 2 = X 1 2 + X 2 2 + … . + X n 2 X^2=X_1^2+X_2^2+\ldots .+X_n^2 X 2 = X 1 2 + X 2 2 + … . + X n 2 遵循卡平方分布 。
等等,我们的观测值( 39 , 15 , 21 , 25 39,15,21,25 39 , 15 , 21 , 25
如果它们服从正态分布,它们就可以转换为标准正态分布。因为正态分布中的任何一点 ( x ) (x) ( x ) z = ( x − z=(x- z = ( x − ) / s t d ) / s t d ) / s t d ( z ) ( z ) ( z )
那么我们的观测值( 39 , 15 , 21 , 25 39,15,21,25 39 , 15 , 21 , 25
这就涉及到本章第六篇介绍的:大数定律与中心极限定理 的内容了。
根据大数定律与中心极限定理(CLT),如果从一个总体中抽取足够大的样本(一般认为样本量大于30),不论总体是什么分布,但是样本的均值 都会趋于正态分布。
因此,上面例子里,我们的平均值(39 , 15 , 21 , 25 39,15,21,25 39 , 15 , 21 , 25 数据本身 的意义。如果是这样的话,我们为什么要假设这些数据遵循正态分布呢?
让我们来仔细看看我们的列联表。
你能从这里看出伯努利试验的影子吗? 是的。因为每个变量(吸烟和不吸烟)都有两种 可能的结果 ("患肺癌"和"未患肺癌")。
从二项分布的角度来看,患者总数为 n n n 54 / 100 54 / 100 54/100 60 / 100 60 / 100 60/100 p p p
在二项分布中,随着 n n n X i X_i X i μ = n p \mu=n p μ = n p σ = n p ( 1 − p ) ) \sigma=\sqrt{n p(1-p))} σ = n p ( 1 − p )) 此处
对于足够大的 n n n n n n p p p μ = n p \mu=n p μ = n p σ = n p ( 1 − p ) ) \sigma=\sqrt{n p(1-p))} σ = n p ( 1 − p ))
让我们把以上这些知识点串连起来。
首先,二项分布告诉我们:一个事件如果只有两个结果:成功和不成功,可以使用二项分布建模,当我们抽样时,如果样品足够大,二项分布会越来越接近正态分布。 因此,我们可以认为我们是从正态分布里取样。那么,(观测值-期望值)也将遵循正态分布,因为 E 是一个常数。那么,使用卡平方分布来检验统计量就完全合理了,因为卡平方分布是n个标准正态分布的平方和。
再次理解自由度 卡方分布的定义是
X 2 = X 1 2 + X 2 2 + … . + X n 2 X^2=X_1^2+X_2^2+\ldots .+X_n^2 X 2 = X 1 2 + X 2 2 + … . + X n 2 而在上节推导的卡方分布公式是
\begin{aligned}
\chi^2 & =\dfrac{n \mu_{A B}^2}{p_A p_B}+\dfrac{n \mu_{\bar{A} B}^2}{p_\bar{A} p_B}+\dfrac{n \mu_{A \bar{B}}^2}{p_A p_\bar{B}}+\dfrac{n \mu_{\bar{A} \bar{B}}^2}{p_\bar{A} p_\bar{B}}
\end{aligned}
从这里看,上面吸烟肺癌的例子里,自由度应该为4,为什么是1呢
我们再次看一下 2 乘 2 的列联表。我们知道样本总数。在这种情况下, 自由度是多少?是 1。为什么? 因为一旦你知道了 2 乘 2 表中的一个数字,那么表中的其他单元格也就确定了,因为有了总数。
比如一共100人,如果我知道有54人吸烟,那么就知道46人不吸烟。同样,如果我知道60人患肺癌,那么就知道40人不患肺癌。
所以,对于一个有 r r r c c c = ( r − 1 ) ( c − 1 ) =(r-1)(c-1) = ( r − 1 ) ( c − 1 ) 2 × 2 2 \times 2 2 × 2
卡方分布的密度函数 χ 2 ( n ) \chi^2(n) χ 2 ( n )
f ( y ) = { 1 2 n / 2 Γ ( n / 2 ) y n 2 − 1 e − 1 2 y , y > 0 0 , y ⩽ 0 , f(y)=\left\{\begin{array}{ll}
\dfrac{1}{2^{n / 2} \Gamma(n / 2)} y^{\frac{n}{2}-1} e^{-\frac{1}{2} y}, & y>0 \\
0, & y \leqslant 0
\end{array},\right. f ( y ) = ⎩ ⎨ ⎧ 2 n /2 Γ ( n /2 ) 1 y 2 n − 1 e − 2 1 y , 0 , y > 0 y ⩽ 0 , 其中, Γ ( ⋅ ) \Gamma(\cdot) Γ ( ⋅ ) f ( y ) f(y) f ( y ) n = 1 , 4 , 9 n=1,4,9 n = 1 , 4 , 9
自由度 卡方分布一个重要参数是自由度,也就是是由几个正态函数相加的。从上图可以看到,自由度为1,2和 3,4,5... 很不同,而且自由度越大,越接近正态分布。比如抽查产品包装是否合格,抽查了4次,自由度就是4.
不同自由度适用于不同检验场景 :在拟合优度检验中,自由度通常等于类别数减1 1 1 卡方检验
在独立性检验中,自由度等于(行数− 1 -1 − 1 − 1 -1 − 1 3 3 3 2 2 2 ( 3 − 1 ) × ( 2 − 1 ) = 2 (3 - 1)\times(2 - 1)= 2 ( 3 − 1 ) × ( 2 − 1 ) = 2
如果是用χ²分布,自由度为k
χ 2 \chi^2 χ 2 由定义可知,若 X 1 , X 2 X_1, X_2 X 1 , X 2 N ( 0 , 1 ) N(0,1) N ( 0 , 1 ) X 1 2 ∼ χ 2 ( 1 ) X_1^2 \sim \chi^2(1) X 1 2 ∼ χ 2 ( 1 ) 2 X 2 2 ∼ χ 2 ( 1 ) 2 X_2^2 \sim \chi^2(1) 2 X 2 2 ∼ χ 2 ( 1 ) X 1 2 + X 2 2 ∼ χ 2 ( 2 ) X_1^2+X_2^2 \sim \chi^2(2) X 1 2 + X 2 2 ∼ χ 2 ( 2 )
χ 2 \chi^2 χ 2 (1)χ 2 \chi^2 χ 2 Y ∼ χ 2 ( n ) Y \sim \chi^2(n) Y ∼ χ 2 ( n ) E ( Y ) = n , D ( Y ) = 2 n E(Y)=n, D(Y)=2 n E ( Y ) = n , D ( Y ) = 2 n χ 2 \chi^2 χ 2 X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X \sim \chi^2(m), Y \sim \chi^2(n) X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X X X Y Y Y X + Y ∼ χ 2 ( m + n ) X+Y \sim \chi^2(m+n) X + Y ∼ χ 2 ( m + n )
证明:(1): E ( Y ) = n , D ( Y ) = 2 n E(Y)=n, D(Y)=2 n E ( Y ) = n , D ( Y ) = 2 n
由 χ 2 \chi^2 χ 2
E ( Y ) = E ( ∑ i = 1 n X i 2 ) = ∑ i = 1 n E ( X i 2 ) = n ( D ( X 1 ) + E 2 ( X 1 ) ) = n D ( Y ) = D ( ∑ i = 1 n X i 2 ) = ∑ i = 1 n D ( X i 2 ) = n ( E ( X 1 4 ) − E 2 ( X 1 2 ) ) = n ( 3 − 1 ) = 2 n \begin{aligned}
E(Y) & =E\left(\sum_{i=1}^n X_i^2\right)=\sum_{i=1}^n E\left(X_i^2\right) \\
& =n\left(D\left(X_1\right)+E^2\left(X_1\right)\right)=n \\
D(Y) & =D\left(\sum_{i=1}^n X_i^2\right)=\sum_{i=1}^n D\left(X_i^2\right) \\
& =n\left(E\left(X_1^4\right)-E^2\left(X_1^2\right)\right)=n(3-1)=2 n
\end{aligned} E ( Y ) D ( Y ) = E ( i = 1 ∑ n X i 2 ) = i = 1 ∑ n E ( X i 2 ) = n ( D ( X 1 ) + E 2 ( X 1 ) ) = n = D ( i = 1 ∑ n X i 2 ) = i = 1 ∑ n D ( X i 2 ) = n ( E ( X 1 4 ) − E 2 ( X 1 2 ) ) = n ( 3 − 1 ) = 2 n (3): 设 X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X \sim \chi^2(m), Y \sim \chi^2(n) X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X X X Y Y Y χ 2 \chi^2 χ 2 X = ∑ i = 1 m X i 2 ; Y = ∑ i = 1 n Y i 2 , X=\sum_{i=1}^m X_i^2 ; Y=\sum_{i=1}^n Y_i^2 , X = ∑ i = 1 m X i 2 ; Y = ∑ i = 1 n Y i 2 , X 1 , ⋯ , X m , Y 1 , ⋯ , Y n X_1, \cdots, X_m, Y_1, \cdots, Y_n X 1 , ⋯ , X m , Y 1 , ⋯ , Y n
X + Y = ∑ i = 1 m X i 2 + ∑ i = 1 n Y i 2 ∼ χ 2 ( m + n ) . X+Y=\sum_{i=1}^m X_i^2+\sum_{i=1}^n Y_i^2 \sim \chi^2(m+n) . X + Y = i = 1 ∑ m X i 2 + i = 1 ∑ n Y i 2 ∼ χ 2 ( m + n ) . 如何理解卡方分布? 下面通过简单例子来理解卡方分布,假设有一批化肥服从 X ∼ ( 50 , 2 2 ) X \sim (50,2^2) X ∼ ( 50 , 2 2 ) 48 − 52 48-52 48 − 52 μ = 50 , σ = 2 \mu=50,\sigma=2 μ = 50 , σ = 2 48 , 49.5 , 50 , 50.5 , 50.5 48,49.5,50,50.5,50.5 48 , 49.5 , 50 , 50.5 , 50.5 ( X − μ ) / σ (X-\mu)/\sigma ( X − μ ) / σ X ∼ N ( 0 , 1 ) X \sim N(0,1) X ∼ N ( 0 , 1 ) − 1 , − 0.25 , 0 , 0.25 , 0.25 -1,-0.25,0,0.25,0.25 − 1 , − 0.25 , 0 , 0.25 , 0.25 ( − 1 ) 2 + ( − 0.25 ) 2 + 0 2 + 0.25 2 + 0.25 2 (-1)^2 + (-0.25)^2 +0^2 +0.25^2 +0.25^2 ( − 1 ) 2 + ( − 0.25 ) 2 + 0 2 + 0.2 5 2 + 0.2 5 2 χ 2 \chi^2 χ 2
从这个定义,我们直接就能推断出两件事情:
第一 ,卡方变量都是正的。(当然,你见过那个平方和是负数么?,平方后相当于方差,抹平了负号的影响); 下图显示了n=1的密度函数图像
第二 ,随着自由度n的增加,卡方分布会往坐标轴右边移动,并且会逐渐变成对称分布。(n增大,表明累加的平方越多,数值越大,当然往坐标轴的右边移动啦)。
第三 n增大,意味着在正态分布的中间值 取到的得越多,所以,卡方分布也会变成中间鼓两边扁的对称分布。
如何理解卡方分布的期望? 卡方分布的数学期望为n n n E ( χ 2 ) = n E(\chi^2)=n E ( χ 2 ) = n n n n n n n
下面给出的是简表。
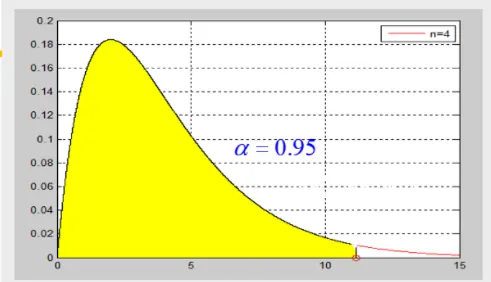
χ 2 \chi^2 χ 2 设 X ∼ χ 2 ( n ) X \sim \chi^2(n) X ∼ χ 2 ( n ) α \alpha α χ α 2 ( n ) \chi_\alpha^2(n) χ α 2 ( n ) χ α 2 ( n ) \chi_\alpha^2(n) χ α 2 ( n ) P ( X ≤ χ α 2 ( n ) ) = α P\left(X \leq \chi_\alpha^2(n)\right)=\alpha P ( X ≤ χ α 2 ( n ) ) = α
分位数值可查表得到,比如 χ 0.95 2 ( 4 ) = 9.488 \chi_{0.95}^2(4)=9.488 χ 0.95 2 ( 4 ) = 9.488
下表给出概率值p p p χ 2 \chi^2 χ 2 p = 0.05 p=0.05 p = 0.05
卡方分布的分位数和正态分布的分位数意思一样,详细点击附录1:置信区间与上α \alpha α
例题 例 设 X 1 , ⋯ , X 6 X_1, \cdots, X_6 X 1 , ⋯ , X 6 N ( 0 , 1 ) N(0,1) N ( 0 , 1 )
Y = ( X 1 + X 2 + X 3 ) 2 + ( X 4 + X 5 + X 6 ) 2 , Y=\left(X_1+X_2+X_3\right)^2+\left(X_4+X_5+X_6\right)^2, Y = ( X 1 + X 2 + X 3 ) 2 + ( X 4 + X 5 + X 6 ) 2 , 试求常数 C C C C Y C Y C Y χ 2 \chi^2 χ 2 X 1 + X 2 + X 3 ∼ N ( 0 , 3 ) , X 4 + X 5 + X 6 ∼ N ( 0 , 3 ) X_1+X_2+X_3 \sim N(0,3), \quad X_4+X_5+X_6 \sim N(0,3) X 1 + X 2 + X 3 ∼ N ( 0 , 3 ) , X 4 + X 5 + X 6 ∼ N ( 0 , 3 )
X 1 + X 2 + X 3 3 ∼ N ( 0 , 1 ) , X 4 + X 5 + X 6 3 ∼ N ( 0 , 1 ) , \frac{X_1+X_2+X_3}{\sqrt{3}} \sim N(0,1), \quad \frac{X_4+X_5+X_6}{\sqrt{3}} \sim N(0,1), 3 X 1 + X 2 + X 3 ∼ N ( 0 , 1 ) , 3 X 4 + X 5 + X 6 ∼ N ( 0 , 1 ) , 且相互独立,于是
( X 1 + X 2 + X 3 3 ) 2 + ( X 4 + X 5 + X 6 3 ) 2 ∼ χ 2 ( 2 ) \left(\frac{X_1+X_2+X_3}{\sqrt{3}}\right)^2+\left(\frac{X_4+X_5+X_6}{\sqrt{3}}\right)^2 \sim \chi^2(2) ( 3 X 1 + X 2 + X 3 ) 2 + ( 3 X 4 + X 5 + X 6 ) 2 ∼ χ 2 ( 2 ) 故应取 C = 1 3 C=\frac{1}{3} C = 3 1 1 3 Y ∼ χ 2 ( 2 ) \frac{1}{3} Y \sim \chi^2(2) 3 1 Y ∼ χ 2 ( 2 )
例设 ( X 1 , X 2 , ⋯ , X 6 ) \left(X_1, X_2, \cdots, X_6\right) ( X 1 , X 2 , ⋯ , X 6 ) N ( 0 , 1 ) N(0,1) N ( 0 , 1 ) X 1 2 + X 2 2 X_1^2+X_2^2 X 1 2 + X 2 2 X 1 2 X_1^2 X 1 2 Q = X 1 2 + a ( X 2 + X 3 ) 2 + b ( X 4 − X 5 + X 6 ) 2 Q=X_1^2+a\left(X_2+X_3\right)^2+b\left(X_4-X_5+X_6\right)^2 Q = X 1 2 + a ( X 2 + X 3 ) 2 + b ( X 4 − X 5 + X 6 ) 2 X 1 , X 2 , ⋯ , X 6 X_1, X_2, \cdots, X_6 X 1 , X 2 , ⋯ , X 6 N ( 0 , 1 ) N(0,1) N ( 0 , 1 ) χ 2 \chi^2 χ 2 X 1 2 + X 2 2 ∼ χ 2 ( 2 ) X_1^2+X_2^2 \sim \chi^2(2) X 1 2 + X 2 2 ∼ χ 2 ( 2 ) X 1 2 ∼ χ 2 ( 1 ) X_1^2 \sim \chi^2(1) X 1 2 ∼ χ 2 ( 1 ) X 2 + X 3 ∼ N ( 0 , 2 ) ⇒ X 2 + X 3 2 ∼ N ( 0 , 1 ) X_2+X_3 \sim N(0,2) \Rightarrow \frac{X_2+X_3}{\sqrt{2}} \sim N(0,1) X 2 + X 3 ∼ N ( 0 , 2 ) ⇒ 2 X 2 + X 3 ∼ N ( 0 , 1 )
X 4 − X 5 + X 6 ∼ N ( 0 , 3 ) ⇒ X 4 − X 5 + X 6 3 ∼ N ( 0 , 1 ) , X_4-X_5+X_6 \sim N(0,3) \Rightarrow \frac{X_4-X_5+X_6}{\sqrt{3}} \sim N(0,1) \text {, } X 4 − X 5 + X 6 ∼ N ( 0 , 3 ) ⇒ 3 X 4 − X 5 + X 6 ∼ N ( 0 , 1 ) , 且 X 1 , 1 2 ( X 2 + X 3 ) , 1 3 ( X 4 − X 5 + X 6 ) X_1, \frac{1}{\sqrt{2}}\left(X_2+X_3\right), \frac{1}{\sqrt{3}}\left(X_4-X_5+X_6\right) X 1 , 2 1 ( X 2 + X 3 ) , 3 1 ( X 4 − X 5 + X 6 ) χ 2 \chi^2 χ 2
X 1 2 + ( X 2 + X 3 2 ) 2 + ( X 4 − X 5 + X 6 3 ) 2 ∼ χ 2 ( 3 ) . X_1^2+\left(\frac{X_2+X_3}{\sqrt{2}}\right)^2+\left(\frac{X_4-X_5+X_6}{\sqrt{3}}\right)^2 \sim \chi^2(3) . X 1 2 + ( 2 X 2 + X 3 ) 2 + ( 3 X 4 − X 5 + X 6 ) 2 ∼ χ 2 ( 3 ) . 可得 a = 1 2 , b = 1 3 a=\frac{1}{2}, b=\frac{1}{3} a = 2 1 , b = 3 1
例设 X 1 , ⋯ , X n X_1, \cdots, X_n X 1 , ⋯ , X n N ( 0 , σ 2 ) N\left(0, \sigma^2\right) N ( 0 , σ 2 ) 1 σ 2 ∑ i = 1 n X i 2 ∼ χ 2 ( n ) \frac{1}{\sigma^2} \sum_{i=1}^n X_i^2 \sim \chi^2(n) σ 2 1 ∑ i = 1 n X i 2 ∼ χ 2 ( n ) 1 n σ 2 ( ∑ i = 1 n X i ) 2 ∼ χ 2 ( 1 ) \frac{1}{n \sigma^2}\left(\sum_{i=1}^n X_i\right)^2 \sim \chi^2(1) n σ 2 1 ( ∑ i = 1 n X i ) 2 ∼ χ 2 ( 1 )
证明 (1) X i σ , i = 1 , ⋯ , n \frac{X_i}{\sigma}, i=1, \cdots, n σ X i , i = 1 , ⋯ , n N ( 0 , 1 ) N (0,1) N ( 0 , 1 ) χ ′ \chi^{\prime} χ ′ ∑ i = 1 n ( X i σ ) 2 ∼ χ 2 ( n ) \sum_{i=1}^n\left(\frac{X_i}{\sigma}\right)^2 \sim \chi^2(n) ∑ i = 1 n ( σ X i ) 2 ∼ χ 2 ( n ) 1 σ 2 ∑ i = 1 n X i 2 ∼ χ 2 ( n ) \frac{1}{\sigma^2} \sum_{i=1}^n X_i^2 \sim \chi^2(n) σ 2 1 ∑ i = 1 n X i 2 ∼ χ 2 ( n )
(2)易见, ∑ i = 1 n X i ∼ N ( 0 , n σ 2 ) \sum_{i=1}^n X_i \sim N\left(0, n \sigma^2\right) ∑ i = 1 n X i ∼ N ( 0 , n σ 2 ) ∑ i = 1 n X i n σ 2 ∼ N ( 0 , 1 ) \frac{\sum_{i=1}^n X_i}{\sqrt{n \sigma^2}} \sim N(0,1) n σ 2 ∑ i = 1 n X i ∼ N ( 0 , 1 ) χ 2 \chi^2 χ 2 ( ∑ i = 1 n X i n σ 2 ) 2 ∼ χ 2 ( 1 ) \left(\frac{\sum_{i=1}^n X_i}{\sqrt{n \sigma^2}}\right)^2 \sim \chi^2(1) ( n σ 2 ∑ i = 1 n X i ) 2 ∼ χ 2 ( 1 ) 1 n σ 2 ( ∑ i = 1 n X i ) 2 ∼ χ 2 ( 1 ) \frac{1}{n \sigma^2}\left(\sum_{i=1}^n X_i\right)^2 \sim \chi^2(1) n σ 2 1 ( ∑ i = 1 n X i ) 2 ∼ χ 2 ( 1 )
例 设 ( X 1 , X 2 , ⋯ , X n ) \left(X_1, X_2, \cdots, X_n\right) ( X 1 , X 2 , ⋯ , X n ) X ∼ χ 2 ( n ) X \sim \chi^2(n) X ∼ χ 2 ( n ) X ˉ = 1 n ∑ i = 1 n X i \bar{X}=\frac{1}{n} \sum_{i=1}^n X_i X ˉ = n 1 ∑ i = 1 n X i E ( X ˉ ) , D ( X ˉ ) E(\bar{X}), D(\bar{X}) E ( X ˉ ) , D ( X ˉ )
解 由 χ 2 \chi^2 χ 2 E ( X ) = n , D ( X ) = 2 n E(X)=n, D(X)=2 n E ( X ) = n , D ( X ) = 2 n
E ( X ˉ ) = E ( 1 n ∑ i = 1 n X i ) = 1 n ∑ i = 1 n E ( X i ) = n . E(\bar{X})=E\left(\frac{1}{n} \sum_{i=1}^n X_i\right)=\frac{1}{n} \sum_{i=1}^n E\left(X_i\right)=n . E ( X ˉ ) = E ( n 1 i = 1 ∑ n X i ) = n 1 i = 1 ∑ n E ( X i ) = n . 由 χ 2 \chi^2 χ 2 E ( X ) = n , D ( X ) = 2 n E(X)=n, D(X)=2 n E ( X ) = n , D ( X ) = 2 n
D ( X ˉ ) = D ( 1 n ∑ i = 1 n X i ) = 1 n 2 D ( ∑ i = 1 n X i ) = 1 n 2 ∑ i = 1 n D ( X i ) = 1 n D ( X ) = 2. \begin{aligned}
D(\bar{X}) & =D\left(\frac{1}{n} \sum_{i=1}^n X_i\right)=\frac{1}{n^2} D\left(\sum_{i=1}^n X_i\right) \\
& =\frac{1}{n^2} \sum_{i=1}^n D\left(X_i\right)=\frac{1}{n} D(X)=2 .
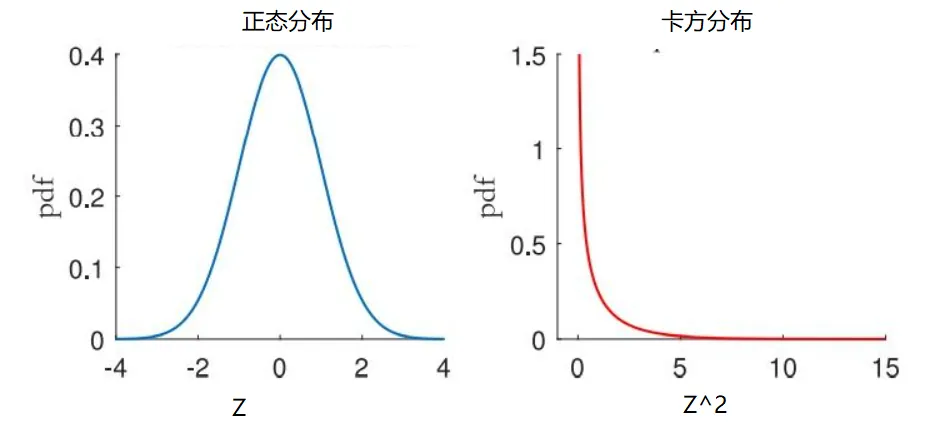
\end{aligned} D ( X ˉ ) = D ( n 1 i = 1 ∑ n X i ) = n 2 1 D ( i = 1 ∑ n X i ) = n 2 1 i = 1 ∑ n D ( X i ) = n 1 D ( X ) = 2. 卡方分布和正态分布的区别 一个随机变量Z Z Z Z ∼ N ( μ = 0 , σ 2 = 1 ) Z \sim N\left(\mu=0, \sigma^2=1\right) Z ∼ N ( μ = 0 , σ 2 = 1 ) Z 2 Z^2 Z 2 Z Z Z Z 2 Z^2 Z 2 Z Z Z E ( Z ) = 0 E (Z)=0 E ( Z ) = 0 Z 2 Z^2 Z 2 E ( Z 2 ) = 1 E\left(Z^2\right)=1 E ( Z 2 ) = 1 D ( Z ) = 1 D(Z)=1 D ( Z ) = 1 Z 2 Z^2 Z 2 D ( Z 2 ) = 2 D\left(Z^2\right)=2 D ( Z 2 ) = 2 Z 2 Z^2 Z 2 Z 2 Z^2 Z 2
因此,转换后的随机变量 Z 2 Z^2 Z 2 Z 1 , Z 2 , … , Z k Z_1, Z_2, \ldots, Z_k Z 1 , Z 2 , … , Z k Z k ∼ N ( 0 , 1 ) Z_k \sim N(0,1) Z k ∼ N ( 0 , 1 )
χ k 2 = Z 1 2 + Z 2 2 + … + Z k 2 \chi_k^2=Z_1^2+Z_2^2+\ldots+Z_k^2 χ k 2 = Z 1 2 + Z 2 2 + … + Z k 2 是一个具有k个自由度的卡方分布
 {width=600px}
{width=600px} {width=600px}
{width=600px}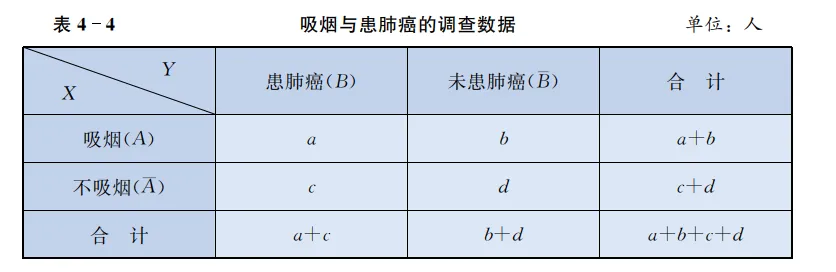 {width=600px}
{width=600px}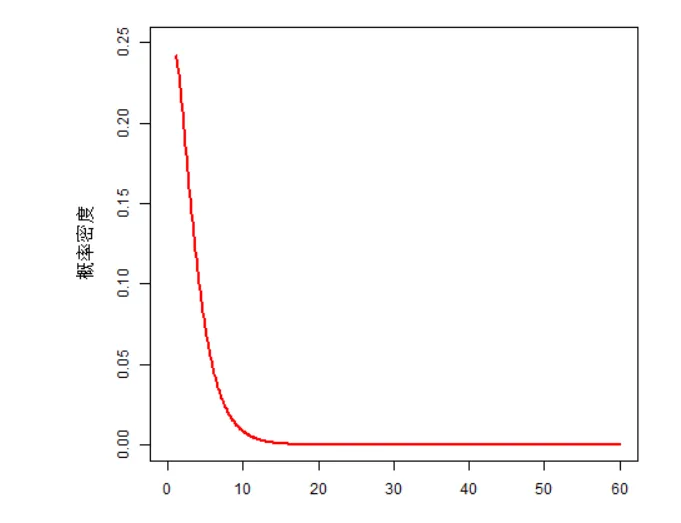 {width=500px}
{width=500px}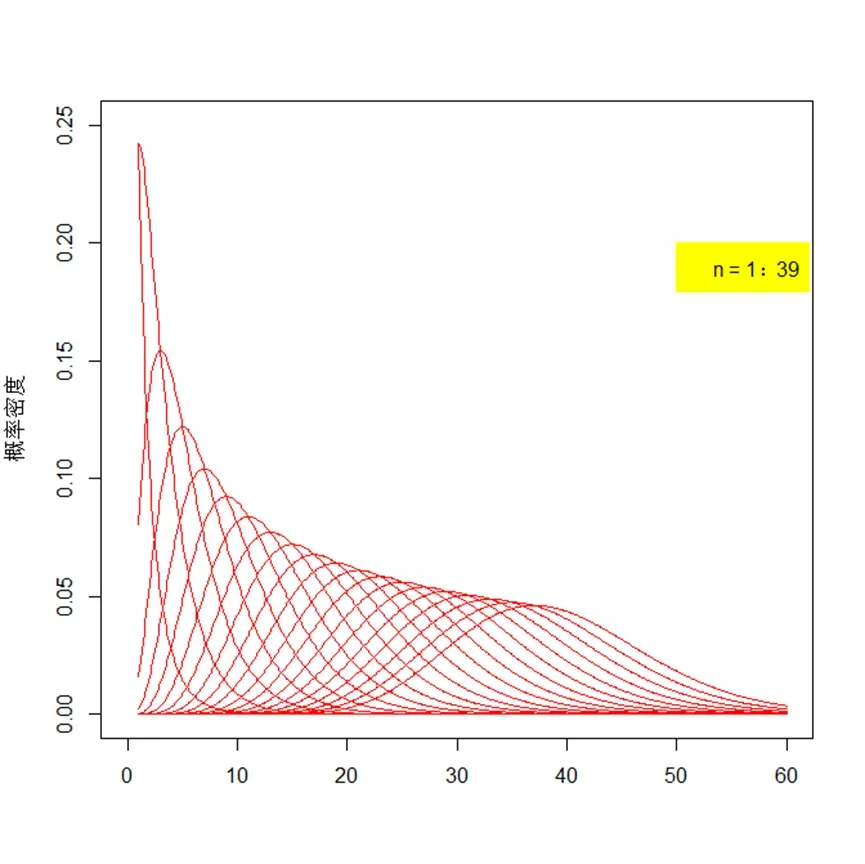 {width=500px}
{width=500px}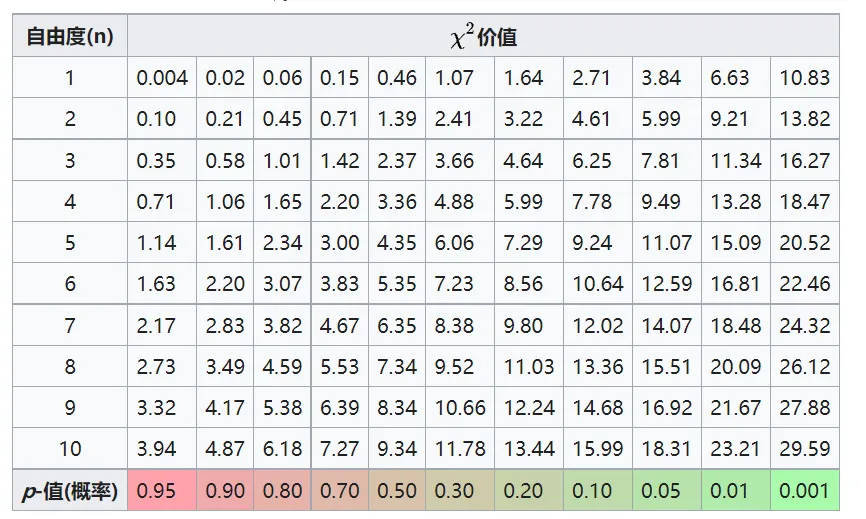
 {width=500px}
同样,随机变量Z的方差是 ,而转换后的随机变量 的方差是 。除了平均值和方差,分布的形状也发生了变化。变换后的变量 的分布不再是对称的了。事实上,分布是向一边倾斜的。此外,随机变量 只能取正值,而随机变量Z也可以取负值(注意上图中两幅图的X轴)。由于新的变换只基于一个参数(Z),所以这个变换的自由度是1。
{width=500px}
同样,随机变量Z的方差是 ,而转换后的随机变量 的方差是 。除了平均值和方差,分布的形状也发生了变化。变换后的变量 的分布不再是对称的了。事实上,分布是向一边倾斜的。此外,随机变量 只能取正值,而随机变量Z也可以取负值(注意上图中两幅图的X轴)。由于新的变换只基于一个参数(Z),所以这个变换的自由度是1。