18._积的分布 - 概率论与数理统计

积的分布

类似商的分布，可得积的分布．设 $(X, Y)$ 具有密度函数 $f(x, y)$ ，则 $Z=X Y$ 的概率密度为

f_Z(z)=\int_{-\infty}^{\infty} f\left(x, \frac{z}{x}\right) \frac{1}{|x|} d x .

例 设二维随机向量 $(X, Y)$ 在矩形 $G=\{(x, y) \mid 0 \leqslant x \leqslant 2,0 \leqslant y \leqslant 1\}$ 上服从均匀分布，试求边长为 $X$ 和 $Y$ 的矩形面积 $S$ 的密度函数 $f(s)$ ． $图片$

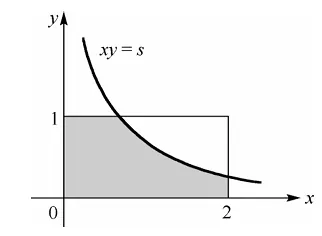
解：二维随机变量 $(X, Y)$ 的密度函数为 $f(x, y)=\left\{\begin{array}{ll}1 / 2, & (x, y) \in G \\ 0, & (x, y) \notin G\end{array}\right.$ ，于是

f_S(s)=\int_{-\infty}^{+\infty} f\left(z, \frac{s}{z}\right) \frac{1}{|z|} d z

因为仅当 $0<z \leqslant 2,0 \leqslant \frac{s}{z} \leqslant 1$ 时， $f\left(z, \frac{s}{z}\right) \neq 0$ ，所以

f_S(s)=\int_{-\infty}^{+\infty} f\left(z, \frac{s}{z}\right) d z=\int_s^2 \frac{1}{2} \cdot \frac{1}{z} d z=\frac{1}{2}(\ln 2-\ln s), 0<s<2 .

其他情形， $f_S(s)=0$ 。从而

f(s)=F^{\prime}(s)=\left\{\begin{array}{ll} (\ln 2-\ln s) / 2, & 0<s<2 \\ 0, & \text { 其他 } \end{array} .\right.