在《概率论与数理统计》这门课里,初学者遇到第一个难懂的概念就是密度函数和分布函数,有概率就行了,为啥还要搞这么多复杂的概念。这是因为,我们要研究现实的世界,而很多分布我们是不清楚的,我们唯一能做的就是:统计。由统计得来的数字来逆推 物态所呈现的可能的概率。比如仍一个硬币,通过观察他的正反面,发现他和我们“库”里的0-1分布很像,那我们就说,仍硬币就服从0-1分布,而不是正态分布,通过大量的经验,我们知道,概率分布可能很多,但是常见的就那几个:一维的包括:二项分布,泊松分布,指数分布,正态分布,而二维的包括均匀分布和正态分布。 换句话说我们学“随机变量与分布”核心是掌握这几个分布的概念和性质 ,一则这几个分布是最常用的分布,基本上够以后工作使用了,另外一则,学会了这几个分布的学习方法,就算遇到不熟悉的分布,也能自学。记住应用场景很重要,比如一本书的印刷错误主要服从泊松分布 ,比如测量产品的误差服从正态分布 ,比如电子设备的寿命服从指数分布 ,而指数分布无记忆性。我们学习概率论,就是学会了解每个分布分布特点,数学期望与方差,记住他们密度函数的图像特点,相反并不需要你记住密度函数或者分布函数的表达式(考研的例外)。
在二维分布里,主要掌握两个分布:二维均匀分布和二维正态分布,上一节介绍了二维均匀分布,接下来介绍二维正态分布。
二维正态分布 如果 ( X , Y ) (X, Y) ( X , Y )
\boxed{
\begin{aligned}
& f(x, y)=\frac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}} \cdot e^ \left\{-\dfrac{1}{2\left(1-\rho^2\right)}\left[\dfrac{\left(x-\mu_1\right)^2}{\sigma_1^2}-\dfrac{2 \rho\left(x-\mu_1\right)\left(y-\mu_2\right)}{\sigma_1 \sigma_2}+\dfrac{\left(y-\mu_2\right)^2}{\sigma_2^2}\right]\right\}
\end{aligned}
}
其中,μ 1 , μ 2 , σ 1 , σ 2 , ρ \mu_1, \mu_2, \sigma_1, \sigma_2, \rho μ 1 , μ 2 , σ 1 , σ 2 , ρ σ 1 > 0 , σ 2 > 0 , − 1 < ρ < 1 \sigma_1>0, \sigma_2>0,-1<\rho<1 σ 1 > 0 , σ 2 > 0 , − 1 < ρ < 1 X , Y X, Y X , Y μ 1 , μ 2 , σ 1 , σ 2 , ρ \mu_1, \mu_2, \sigma_1, \sigma_2, \rho μ 1 , μ 2 , σ 1 , σ 2 , ρ 二维正态分布 ,记为 ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) (X, Y) \sim N\left(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \rho\right) ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ )
定义域中− ∞ < x < + ∞ , − ∞ < y < + ∞ -\infty < x < +\infty,-\infty < y < +\infty − ∞ < x < + ∞ , − ∞ < y < + ∞
− ∞ < μ 1 , μ 2 < + ∞ , σ 1 , σ 2 > 0 , ∣ ρ ∣ < 1 , -\infty<\mu_1, \mu_2<+\infty, \sigma_1, \sigma_2>0,|\rho|<1, − ∞ < μ 1 , μ 2 < + ∞ , σ 1 , σ 2 > 0 , ∣ ρ ∣ < 1 , 以后将指出: μ 1 , μ 2 \mu_1, \mu_2 μ 1 , μ 2 X X X Y Y Y σ 1 2 , σ 2 2 \sigma_1^2, \sigma_2^2 σ 1 2 , σ 2 2 X X X Y Y Y ρ \rho ρ X X X Y Y Y
二维分布的公式很长,可能吓跑我们,但是记住:我们无需记住密度函数公式,只要掌握它的形状和特点就可以了。(注意:普通考试不需要记住这些公式,但是考研一族例外哦^_^,如果你是考研的需要记住这些公式,甚至下面介绍的推导过程也要会)。
下图显示了二维正态分布的密度函数图像,从图像上看,他就像一个凸起的小山包。二维正态分布的概率密度虽然较复杂,但它是一个在数学、物理和工程等领域都有广泛应用的分布,有“漂亮”的结论,无论在理论研究还是实际应用中都起着至关重要的作用.
特别,当 μ 1 = μ 2 = 0 , σ 1 = σ 2 = 1 \mu_1=\mu_2=0, \sigma_1=\sigma_2=1 μ 1 = μ 2 = 0 , σ 1 = σ 2 = 1 ( X , Y ) (X, Y) ( X , Y )
性质:( X , Y ) ∼ N ( μ 1 , σ 1 2 ; μ 2 , σ 2 2 ; ρ ) ⇒ X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) (X, Y) \sim N\left(\mu_1, \sigma_1^2 ; \mu_2, \sigma_2^2 ; \rho\right) \Rightarrow X \sim N\left(\mu_1, \sigma_1^2\right), Y \sim N\left(\mu_2, \sigma_2^2\right) ( X , Y ) ∼ N ( μ 1 , σ 1 2 ; μ 2 , σ 2 2 ; ρ ) ⇒ X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 )
后面这个性质说明:二维正态联合分布可以唯一决定其每个分量都是正态分布,但反过来不成立。即知道 X X X Y Y Y
N ( 0 , 0 , 1 , 1 , 1 / 2 ) 和 N ( 0 , 0 , 1 , 1 , 1 / 3 ) N(0,0,1,1,1 / 2) \text { 和 } N(0,0,1,1,1 / 3) N ( 0 , 0 , 1 , 1 , 1/2 ) 和 N ( 0 , 0 , 1 , 1 , 1/3 ) 它们的任一边缘分布都是标准正态分布 N ( 0 , 1 ) N(0,1) N ( 0 , 1 ) ρ \rho ρ X X X Y Y Y ρ \rho ρ X X X Y Y Y
后面这个性质可以做一个简单比喻:学生身高服从正态分布,学生体重服从正态分布,所以,学生的“身高和体重”服从二维正态分布基本上是正确的。 学生身高服从正态分布,机器包装产品误差也服从正态分布,我们不能说“学生身高和机器包装误差也服从二维正态分布”,很明显,学生身高和机器包装产品误差是风马牛不相及的两件事。
例 设 ( X , Y ) (X, Y) ( X , Y )
f ( x , y ) = 1 2 π × 10 2 e − x 2 + y 2 2 × 10 2 f(x, y)=\frac{1}{2 \pi \times 10^2} \mathrm{e}^{-\frac{x^2+y^2}{2 \times 10^2}} f ( x , y ) = 2 π × 1 0 2 1 e − 2 × 1 0 2 x 2 + y 2 求 P { Y ⩾ X } P\{Y \geqslant X\} P { Y ⩾ X }
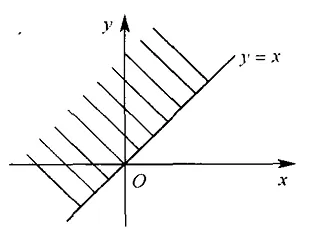
P { Y ⩾ X } = ∬ y ⩾ x f ( x , y ) d x d y P\{Y \geqslant X\}=\iint_{y \geqslant x} f(x, y) \mathrm{d} x \mathrm{~d} y P { Y ⩾ X } = ∬ y ⩾ x f ( x , y ) d x d y { x = r cos θ y = r sin θ \left\{\begin{array}{l}x=r \cos \theta \\ y=r \sin \theta\end{array}\right. { x = r cos θ y = r sin θ
上式 = 1 2 π × 10 2 ∫ π 4 5 π 4 d θ ∫ 0 + ∞ e − r 2 2 × 10 2 r d r = 1 2 × 10 2 ∫ 0 + ∞ e − r 2 2 × 10 2 r d r = 1 2 . \begin{aligned}
\text { 上式 } & =\frac{1}{2 \pi \times 10^2} \int_{\frac{\pi}{4}}^{\frac{5 \pi}{4}} \mathrm{~d} \theta \int_0^{+\infty} \mathrm{e}^{-\frac{r^2}{2 \times 10^2}} r \mathrm{~d} r \\
& =\frac{1}{2 \times 10^2} \int_0^{+\infty} \mathrm{e}^{-\frac{r^2}{2 \times 10^2}} r \mathrm{~d} r=\frac{1}{2} .
\end{aligned} 上式 = 2 π × 1 0 2 1 ∫ 4 π 4 5 π d θ ∫ 0 + ∞ e − 2 × 1 0 2 r 2 r d r = 2 × 1 0 2 1 ∫ 0 + ∞ e − 2 × 1 0 2 r 2 r d r = 2 1 . 看懂二维正态分布密度图 我们在一维平面里说过,概率密度( a , b ) (a,b) ( a , b ) ( a , b ) (a,b) ( a , b ) 此处 , 那么如何理解二维概率密度呢?
首先,我们要明白,二维概率事件是由3个参数决定:比如射靶,我们说“射在(1,2)的概率为0.01”,那么这里就有X = 1 , Y = 2 , Z = 0.01 X=1,Y=2,Z=0.01 X = 1 , Y = 2 , Z = 0.01
这个图形很像农民带的草帽,我们通常称呼这个图形为“草帽”图形。因为密度函数必须大于等于零,所以这个草帽可以认为为平底的,又因为所有射靶所有的概率最多为1,因此,这个概率的体积最大只能为1.
如果我们从俯视图的视角从下看这个草帽,可以发现他的定义域D就是一个二维平面。
想想一下我们用一把刀沿着X , Y X,Y X , Y F ( x , y ) = P ( X ⩽ x , Y ⩽ y ) = ∫ − ∞ x ∫ − ∞ y p ( x , y ) d x d y F(x, y)=P(X \leqslant x, Y \leqslant y)=\int_{-\infty}^{x} \int_{-\infty}^{y} p(x, y) d x d y F ( x , y ) = P ( X ⩽ x , Y ⩽ y ) = ∫ − ∞ x ∫ − ∞ y p ( x , y ) d x d y
如果把二维随机变量 ( X , Y ) (X, Y) ( X , Y ) F ( x , y ) F(x, y) F ( x , y ) ( x , y ) (x, y) ( x , y ) ( X , Y ) (X, Y) ( X , Y ) X = x X=x X = x Y = y Y=y Y = y ( x , y ) (x, y) ( x , y )
二维正态密度图的通俗理解 我们知道,一个学生的身高服从正态分布,一个学生的体重也服从正态分布,如果以身高和体重为参数画在空间坐标里,毫无疑问,身高在 165cm-175cm 之间,体重在 55kg-75kg 之间应该是最多,即中心点应该是最密集的,如下图
如果我们固定一个参数,比如身高,让身高取值为− ∞ < x < + ∞ -\infty < x < +\infty − ∞ < x < + ∞
公式验证 证明:该函数是一个概率密度函数,其应该满足概率密度函数的基本性质:一是大于零,二是全空间上的积分等于 1 。第一点显而易见,下面给出条件二的证明。
做变换
u = 1 1 − ρ 2 ( x 1 − μ 1 σ 1 ) , v = 1 1 − ρ 2 ( x 2 − μ 2 σ 2 ) u=\frac{1}{\sqrt{1-\rho^2}}\left(\frac{x_1-\mu_1}{\sigma_1}\right), v=\frac{1}{\sqrt{1-\rho^2}}\left(\frac{x_2-\mu_2}{\sigma_2}\right) u = 1 − ρ 2 1 ( σ 1 x 1 − μ 1 ) , v = 1 − ρ 2 1 ( σ 2 x 2 − μ 2 ) 得
∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = 1 2 π 1 − ρ 2 ∫ − ∞ + ∞ ∫ − ∞ + ∞ exp [ − 1 2 ( u 2 − 2 ρ u v + v 2 ) ] d u d v \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) d x d y=\frac{1}{2 \pi} \sqrt{1-\rho^2} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \exp \left[-\frac{1}{2}\left(u^2-2 \rho u v+v^2\right)\right] d u d v ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = 2 π 1 1 − ρ 2 ∫ − ∞ + ∞ ∫ − ∞ + ∞ exp [ − 2 1 ( u 2 − 2 ρ uv + v 2 ) ] d u d v 再做变量代换
t 1 = u − ρ v , t 2 = 1 − ρ 2 v t_1=u-\rho v, t_2=\sqrt{1-\rho^2} v t 1 = u − ρ v , t 2 = 1 − ρ 2 v 注意到
得 u 2 − 2 ρ u v + v 2 = ( u − ρ v ) 2 + ( 1 − ρ 2 ) v 2 = t 1 2 + t 2 2 ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = 1 − ρ 2 2 π 1 − ρ 2 ∫ − ∞ + ∞ ∫ − ∞ + ∞ exp [ − 1 2 ( t 1 2 + t 2 2 ) ] d t 1 d t 2 = 1 2 π ∫ − ∞ ∞ exp ( − 1 2 t 1 2 ) d t 1 ∫ − ∞ ∞ exp ( − 1 2 t 2 2 ) d t 2 = 1 2 π 2 π 2 π = 1 \begin{aligned}
&\text { 得 } u^2-2 \rho u v+v^2=(u-\rho v)^2+\left(1-\rho^2\right) v^2=t_1^2+t_2^2\\
&\begin{aligned}
& \quad \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) d x d y=\frac{\sqrt{1-\rho^2}}{2 \pi \sqrt{1-\rho^2}} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \exp \left[-\frac{1}{2}\left(t_1^2+t_2^2\right)\right] d t_1 d t_2 \\
& = \\
& \frac{1}{2 \pi} \int_{-\infty}^{\infty} \exp \left(-\frac{1}{2} t_1^2\right) d t_1 \int_{-\infty}^{\infty} \exp \left(-\frac{1}{2} t_2^2\right) d t_2 \\
& = \\
& \frac{1}{2 \pi} \sqrt{2 \pi} \sqrt{2 \pi}=1
\end{aligned}
\end{aligned} 得 u 2 − 2 ρ uv + v 2 = ( u − ρ v ) 2 + ( 1 − ρ 2 ) v 2 = t 1 2 + t 2 2 ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = 2 π 1 − ρ 2 1 − ρ 2 ∫ − ∞ + ∞ ∫ − ∞ + ∞ exp [ − 2 1 ( t 1 2 + t 2 2 ) ] d t 1 d t 2 = 2 π 1 ∫ − ∞ ∞ exp ( − 2 1 t 1 2 ) d t 1 ∫ − ∞ ∞ exp ( − 2 1 t 2 2 ) d t 2 = 2 π 1 2 π 2 π = 1 哇,好巧,积分正好结果正好是1,其实一点都不巧,比如为什么前面要除以一个2 π 2\pi 2 π
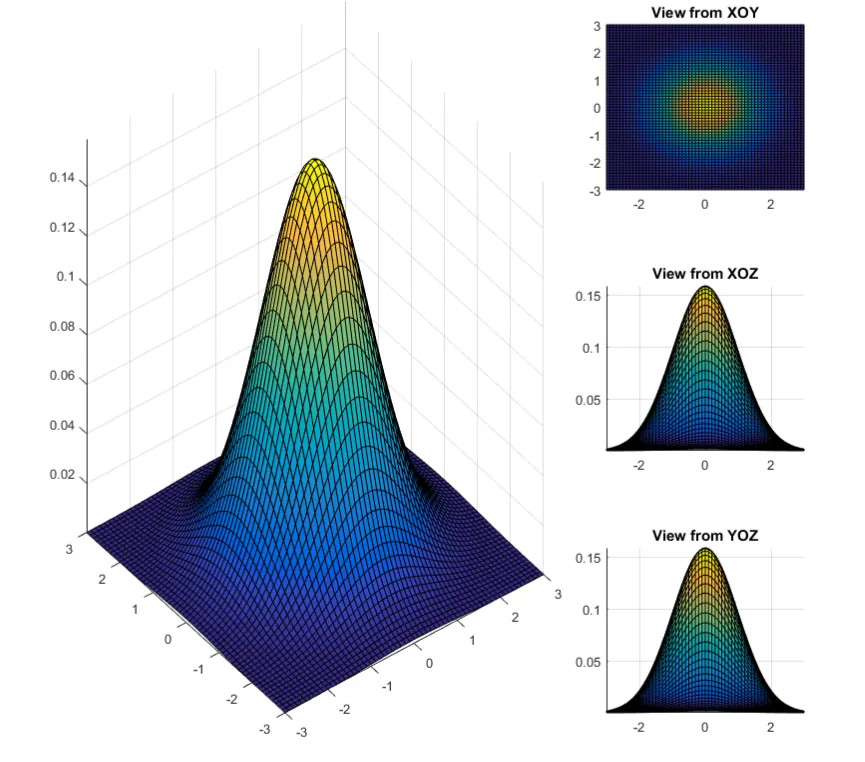
二维正态分布密度函数图像 二维正态密度函数的图形很像一顶四周无限延伸的草帽, 其中心点在 ( μ 1 , μ 2 ) \left(\mu_1, \mu_2\right) ( μ 1 , μ 2 ) x O p x O_p x O p y O p y O_p y O p
从上图看,我们可以看出二维概率密度函数是高度对称的,无论从XOY面,还是XOZ面,还是YOZ面。当然对于这个例子而言,甚至在XOY面上,整个图像还是关于原点中心对称的哦!不过这个可不是所有多维高二维正态分布都满足的哦,这个所谓的中心对称这是因为这个例子太特殊了哈! 若是我们给定均值还是为 0 ,而协方差矩阵变为 Σ = [ 1 , 1 ; 1 , 2 ] \Sigma=[1,1 ; 1,2] Σ = [ 1 , 1 ; 1 , 2 ]
对比两个图和我们给出的协方差矩阵,可以发现,XOY面中心对称的时候,事实上随机向量的两个分量是独立的(协方差矩阵中非对角元素为0),当然也可以说成当两个分量是独立的时候XOY面存在中心对称的情况哦!
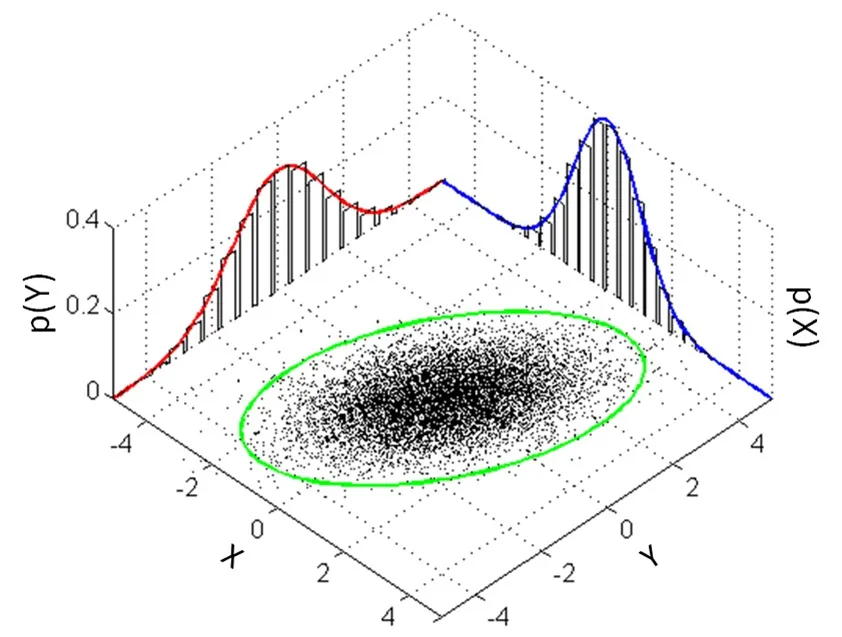
边缘概率密度 二维正态分布的两个边缘分布都是一维正态分布的形式:并且都不依赖于参数 ρ \rho ρ μ 1 , μ 2 , σ 1 , σ 2 \mu_1, \mu_2, \sigma_1, \sigma_2 μ 1 , μ 2 , σ 1 , σ 2 ρ \rho ρ X X X Y Y Y X X X Y Y Y ρ \rho ρ
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 , − ∞ < x < ∞ f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^2}{2 \sigma^2}},-\infty<x<\infty f ( x ) = 2 π σ 1 e − 2 σ 2 ( x − μ ) 2 , − ∞ < x < ∞ 证明 f X ( x ) = ∫ − ∞ ∞ f ( x , y ) d y f_X(x)=\int_{-\infty}^{\infty} f(x, y) d y f X ( x ) = ∫ − ∞ ∞ f ( x , y ) d y ( y − μ 2 ) 2 σ 2 2 − 2 ρ ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 = ( y − μ 2 σ 2 − ρ x − μ 1 σ 1 ) 2 − ρ 2 ( x − μ 1 ) 2 σ 1 2 \frac{\left(y-\mu_2\right)^2}{\sigma_2^2}-2 \rho \frac{\left(x-\mu_1\right)\left(y-\mu_2\right)}{\sigma_1 \sigma_2}=\left(\frac{y-\mu_2}{\sigma_2}-\rho \frac{x-\mu_1}{\sigma_1}\right)^2-\rho^2 \frac{\left(x-\mu_1\right)^2}{\sigma_1^2} σ 2 2 ( y − μ 2 ) 2 − 2 ρ σ 1 σ 2 ( x − μ 1 ) ( y − μ 2 ) = ( σ 2 y − μ 2 − ρ σ 1 x − μ 1 ) 2 − ρ 2 σ 1 2 ( x − μ 1 ) 2
f X ( x ) = 1 2 π σ 1 σ 2 1 − ρ 2 e − ( x − μ 1 ) 2 2 σ 1 2 ∫ − ∞ ∞ e − ( y − μ 2 σ 2 − ρ x − μ 1 σ ) 2 2 ( 1 − ρ 2 ) d y 令 t = 1 1 − ρ 2 ( y − μ 2 σ 2 − ρ x − μ 1 σ 1 ) \begin{aligned}
& f_X(x)=\frac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}} e^{-\frac{\left(x-\mu_1\right)^2}{2 \sigma_1^2}} \int_{-\infty}^{\infty} e^{-\frac{\left(\frac{y-\mu_2}{\sigma_2}-\rho \frac{x-\mu_1}{\sigma}\right)^2}{2\left(1-\rho^2\right)}} d y \\
& \text { 令 } t=\frac{1}{\sqrt{1-\rho^2}}\left(\frac{y-\mu_2}{\sigma_2}-\rho \frac{x-\mu_1}{\sigma_1}\right)
\end{aligned} f X ( x ) = 2 π σ 1 σ 2 1 − ρ 2 1 e − 2 σ 1 2 ( x − μ 1 ) 2 ∫ − ∞ ∞ e − 2 ( 1 − ρ 2 ) ( σ 2 y − μ 2 − ρ σ x − μ 1 ) 2 d y 令 t = 1 − ρ 2 1 ( σ 2 y − μ 2 − ρ σ 1 x − μ 1 ) 则有 f X ( x ) = 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 ∫ − ∞ ∞ e − t 2 2 d t f_X(x)=\frac{1}{2 \pi \sigma_1} e^{-\frac{\left(x-\mu_1\right)^2}{2 \sigma_1^2}} \int_{-\infty}^{\infty} e^{-\frac{t^2}{2}} d t f X ( x ) = 2 π σ 1 1 e − 2 σ 1 2 ( x − μ 1 ) 2 ∫ − ∞ ∞ e − 2 t 2 d t
f X ( x ) = 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 , − ∞ < x < ∞ f_X(x)=\frac{1}{\sqrt{2 \pi} \sigma_1} e^{-\frac{\left(x-\mu_1\right)^2}{2 \sigma_1^2}},-\infty<x<\infty f X ( x ) = 2 π σ 1 1 e − 2 σ 1 2 ( x − μ 1 ) 2 , − ∞ < x < ∞ 同理
f Y ( y ) = 1 2 π σ 2 e − ( y − μ 2 ) 2 2 σ 2 2 , − ∞ < y < ∞ f_Y(y)=\frac{1}{\sqrt{2 \pi} \sigma_2} e^{-\frac{\left(y-\mu_2\right)^2}{2 \sigma_2^2}},-\infty<y<\infty f Y ( y ) = 2 π σ 2 1 e − 2 σ 2 2 ( y − μ 2 ) 2 , − ∞ < y < ∞ 上面这个结论需要记住:二维正态分布的两个边缘分布都是一维正态分布的形式。
独立性 对于二维正态随机变量 ( X , Y ) , X (X, Y), X ( X , Y ) , X Y Y Y ρ = 0 \rho=0 ρ = 0
必要性: 如果 p = 0 f ( x , y ) = 1 2 π σ 1 σ 2 exp [ − 1 2 ( ( x − μ 1 ) 2 σ 1 2 + ( y − μ 2 ) 2 σ 2 2 ) ] p =0 f(x, y)=\frac{1}{2 \pi \sigma_1 \sigma_2} \exp \left[-\frac{1}{2}\left(\frac{\left(x-\mu_1\right)^2}{\sigma_1^2}+\frac{\left(y-\mu_2\right)^2}{\sigma_2^2}\right)\right] p = 0 f ( x , y ) = 2 π σ 1 σ 2 1 exp [ − 2 1 ( σ 1 2 ( x − μ 1 ) 2 + σ 2 2 ( y − μ 2 ) 2 ) ]
f X ( x ) f Y ( y ) = 1 2 π σ 1 σ 2 e − ( x − μ 1 ) 2 2 σ 1 2 − ( y − μ 2 ) 2 2 σ 2 2 f_X(x) f_Y(y)=\frac{1}{2 \pi \sigma_1 \sigma_2} e^{-\frac{\left(x-\mu_1\right)^2}{2 \sigma_1^2}-\frac{\left(y-\mu_2\right)^2}{2 \sigma_2^2}} f X ( x ) f Y ( y ) = 2 π σ 1 σ 2 1 e − 2 σ 1 2 ( x − μ 1 ) 2 − 2 σ 2 2 ( y − μ 2 ) 2 有 f ( x , y ) = f X ( x ) f Y ( y ) f(x, y)=f_X(x) f_Y(y) f ( x , y ) = f X ( x ) f Y ( y ) f ( x , y ) , f X ( x ) , f Y ( y ) f(x, y), f_X(x), f_Y(y) f ( x , y ) , f X ( x ) , f Y ( y ) f ( x , y ) = f X ( x ) f Y ( y ) f(x, y)=f_X(x) f_Y(y) f ( x , y ) = f X ( x ) f Y ( y )
特别令 x = μ 1 , y = μ 2 x=\mu_1, y=\mu_2 x = μ 1 , y = μ 2
1 2 π σ 1 σ 2 1 − ρ 2 = 1 2 π σ 1 σ 2 \frac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}}=\frac{1}{2 \pi \sigma_1 \sigma_2} 2 π σ 1 σ 2 1 − ρ 2 1 = 2 π σ 1 σ 2 1 为使这一等式成立,从而 ρ = 0 \rho=0 ρ = 0
这个结论也需要记住。
二维正态分布常用结论 从二维正态分布公式可以推出如下结论:具体推导可以参考相关书籍,这里给出必须记住的揭露。
【结论1】 若 ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) (X, Y) \sim N\left(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \rho\right) ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) X \sim N\left(\mu_1, \sigma_1^2\right), Y \sim N\left(\mu_2, \sigma_2^2\right) X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) X , Y X, Y X , Y
【易混点】 ( X , Y ) (X, Y) ( X , Y ) ( X , Y (X, Y ( X , Y ( X , Y ) (X, Y) ( X , Y )
【结论2】 若 X , Y X, Y X , Y X , Y X, Y X , Y ( X , Y ) (X, Y) ( X , Y ) X ∼ N ( 0 , 1 ) X \sim N(0,1) X ∼ N ( 0 , 1 ) ( 0 , 1 ) . P X Y = 0 (0,1) . P_{X Y}=0 ( 0 , 1 ) . P X Y = 0
【易混点1】若 X , Y X, Y X , Y X , Y X, Y X , Y η = a X + b Y \eta=a X+b Y η = a X + bY X , Y X, Y X , Y X , Y X, Y X , Y ( X , Y ) (X, Y) ( X , Y )
【结论3】 ( X , Y ) ( X, Y) ( X , Y ) η = a X + b Y \eta=a X+b Y η = a X + bY n n n X = ( X 1 , X 2 , … , X n ) T X=\left(X_1, X_2, \ldots, X_n\right)^T X = ( X 1 , X 2 , … , X n ) T n n n N ( μ , B ) N(\mu, B) N ( μ , B ) Z = ∑ j = 1 n l j X j Z=\sum_{j=1}^n l_j X_j Z = ∑ j = 1 n l j X j ( X 1 , x 2 , ⋯ , X η ) ∼ N ( μ . , Σ ) \left(X_1, x_2, \cdots, X_\eta\right) \sim N(\mu ., \Sigma) ( X 1 , x 2 , ⋯ , X η ) ∼ N ( μ . , Σ )
【结论4】 若 X , Y X, Y X , Y X , Y X, Y X , Y ( X , Y ) (X, Y) ( X , Y )
【结论5】 只要 ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) (X, Y) \sim N\left(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \rho\right) ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) X , Y X, Y X , Y a , b a, b a , b a X + b Y − N ( a μ 1 + b μ 2 , a 2 σ 1 2 + b 2 σ 2 2 + 2 a b ρ σ 1 σ 2 ) a X+b Y-N\left(a \mu_1+b \mu_2, a^2 \sigma_1^2+b^2 \sigma_2^2+2 a b \rho \sigma_1 \sigma_2\right) a X + bY − N ( a μ 1 + b μ 2 , a 2 σ 1 2 + b 2 σ 2 2 + 2 ab ρ σ 1 σ 2 ) X , Y X, Y X , Y ρ = 0 \rho=0 ρ = 0 a X + b Y ∼ N ( a μ 1 + b μ 2 , a 2 σ 1 2 + b 2 σ 2 2 ) a X+b Y \sim N\left(a \mu_1+b \mu_2, a^2 \sigma_1^2+b^2 \sigma_2^2\right) a X + bY ∼ N ( a μ 1 + b μ 2 , a 2 σ 1 2 + b 2 σ 2 2 )
应用背景 生活中有不少二维随机变量是服从二维正态分布的,例如,射击时炮弹的弹着点在平面上的散布或枪弹的弹着点在靶面上的分布都是二维正态分布;又如某种生物的体长和体重一般也服从二维正态分布.
例 设 ( X , Y ) (X, Y) ( X , Y )
f ( x , y ) = 1 2 π × 10 2 e − x 2 + y 2 2 × 10 2 , f(x, y)=\frac{1}{2 \pi \times 10^2} e^{-\frac{x^2+y^2}{2 \times 10^2}}, f ( x , y ) = 2 π × 1 0 2 1 e − 2 × 1 0 2 x 2 + y 2 , 求 P { Y ⩾ X } P\{Y \geqslant X\} P { Y ⩾ X }
= 1 2 π × 10 2 ∫ π 4 5 π 4 d θ ∫ 0 + ∞ e − r 2 2 × 10 2 ⋅ r d r = − 1 2 ∫ 0 + ∞ e − r 2 2 × 10 2 d ( − r 2 2 × 10 2 ) = − 1 2 e − r 2 2 × 10 2 ∣ 0 + ∞ = 1 2 . \begin{aligned}
& =\frac{1}{2 \pi \times 10^2} \int_{\frac{\pi}{4}}^{\frac{5 \pi}{4}} d \theta \int_0^{+\infty} e-\frac{r^2}{2 \times 10^2} \cdot r d r \\
& =-\frac{1}{2} \int_0^{+\infty} e^{-\frac{r^2}{2 \times 10^2}} d\left(-\frac{r^2}{2 \times 10^2}\right)=-\left.\frac{1}{2} e^{-\frac{r^2}{2 \times 10^2}}\right|_0 ^{+\infty} \\
& =\frac{1}{2} .
\end{aligned} = 2 π × 1 0 2 1 ∫ 4 π 4 5 π d θ ∫ 0 + ∞ e − 2 × 1 0 2 r 2 ⋅ r d r = − 2 1 ∫ 0 + ∞ e − 2 × 1 0 2 r 2 d ( − 2 × 1 0 2 r 2 ) = − 2 1 e − 2 × 1 0 2 r 2 0 + ∞ = 2 1 . 这里的难点是大量计算使用二重积分,如果微积分基础不好,很难做正确。
下面这个例题是普通高校期末考试考的内容。
例 若 X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) X \sim N\left(\mu_1, \sigma_1^2\right), Y \sim N\left(\mu_2, \sigma_2^2\right) X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) ( X , Y ) (X, Y) ( X , Y ) ρ = 0 \rho=0 ρ = 0 ( X , Y ) (X, Y) ( X , Y ) ρ \rho ρ ( X , Y ) (X, Y) ( X , Y ) X − Y ∼ N ( μ 1 − μ 2 , σ 1 2 − σ 2 2 ) X-Y \sim N\left(\mu_1-\mu_2, \sigma_1^2-\sigma_2^2\right) X − Y ∼ N ( μ 1 − μ 2 , σ 1 2 − σ 2 2 )
下面这个例题可能属于重点高校期末考试的内容(难度加深)
例 设 ( X , Y ) ∼ N ( 0 , 0 , σ 2 , σ 2 , 0 ) (X, Y) \sim N\left(0,0, \sigma^2, \sigma^2, 0\right) ( X , Y ) ∼ N ( 0 , 0 , σ 2 , σ 2 , 0 ) P ( Y > X ) P(Y>X) P ( Y > X ) f ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 ( − ∞ < x , y < + ∞ ) f(x, y)=\frac{1}{2 \pi \sigma^2} e ^{-\frac{x^2+y^2}{2 \sigma^2}}(-\infty<x, y<+\infty) f ( x , y ) = 2 π σ 2 1 e − 2 σ 2 x 2 + y 2 ( − ∞ < x , y < + ∞ )
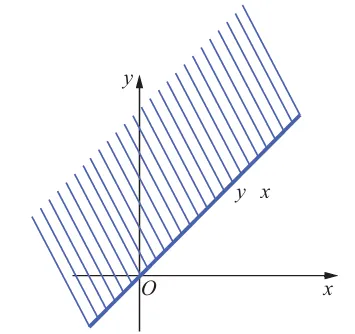
P ( Y > X ) = ∬ x < y 1 2 π σ 2 e − x 2 + y 2 2 σ 2 d x d y . P(Y>X)=\iint_{x<y} \frac{1}{2 \pi \sigma^2} e^{-\frac{x^2+y^2}{2 \sigma^2}} d x d y . P ( Y > X ) = ∬ x < y 2 π σ 2 1 e − 2 σ 2 x 2 + y 2 d x d y . 引进极坐标
x = r cos θ , y = r sin θ , x=r \cos \theta, \quad y=r \sin \theta, x = r cos θ , y = r sin θ , 则
P ( X < Y ) = ∫ π 4 5 π 4 ∫ 0 + ∞ 1 2 π σ 2 r e − r 2 2 σ 2 d r d θ = 1 2 . P(X<Y)=\int_{\frac{\pi}{4}}^{\frac{5 \pi}{4}} \int_0^{+\infty} \frac{1}{2 \pi \sigma^2} r e^{-\frac{r^2}{2 \sigma^2}} d r d \theta=\frac{1}{2} . P ( X < Y ) = ∫ 4 π 4 5 π ∫ 0 + ∞ 2 π σ 2 1 r e − 2 σ 2 r 2 d r d θ = 2 1 . 下面这个例题,是考研一族爱考的内容。
例设二维随机变量 ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) (X, Y) \sim N\left(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \rho\right) ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) ( X , Y ) (X, Y) ( X , Y )
D = { ( x , y ) : ( x − μ 1 ) 2 σ 1 2 − 2 ρ ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 + ( y − μ 2 ) 2 σ 2 2 ⩽ λ 2 } D=\left\{(x, y): \frac{\left(x-\mu_1\right)^2}{\sigma_1^2}-2 \rho \frac{\left(x-\mu_1\right)\left(y-\mu_2\right)}{\sigma_1 \sigma_2}+\frac{\left(y-\mu_2\right)^2}{\sigma_2^2} \leqslant \lambda^2\right\} D = { ( x , y ) : σ 1 2 ( x − μ 1 ) 2 − 2 ρ σ 1 σ 2 ( x − μ 1 ) ( y − μ 2 ) + σ 2 2 ( y − μ 2 ) 2 ⩽ λ 2 } 内的概率.
解 所求概率为
p = 1 2 π σ 1 σ 2 1 − ρ 2 ∬ D exp { − 1 2 ( 1 − ρ 2 ) [ ( x − μ 1 σ 1 ) 2 − 2 ρ ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 + ( y − μ 2 σ 2 ) 2 ] } d x d y \begin{aligned}
p= & \frac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}} \iint_D \exp \left\{-\frac{1}{2\left(1-\rho^2\right)}\left[\left(\frac{x-\mu_1}{\sigma_1}\right)^2-\right.\right. \\
& \left.\left.2 \rho \frac{\left(x-\mu_1\right)\left(y-\mu_2\right)}{\sigma_1 \sigma_2}+\left(\frac{y-\mu_2}{\sigma_2}\right)^2\right]\right\} d x d y
\end{aligned} p = 2 π σ 1 σ 2 1 − ρ 2 1 ∬ D exp { − 2 ( 1 − ρ 2 ) 1 [ ( σ 1 x − μ 1 ) 2 − 2 ρ σ 1 σ 2 ( x − μ 1 ) ( y − μ 2 ) + ( σ 2 y − μ 2 ) 2 ] } d x d y 作变换
{ u = x − μ 1 σ 1 − ρ y − μ 2 σ 2 , v = y − μ 2 σ 2 1 − ρ 2 . \left\{\begin{array}{l}
u=\frac{x-\mu_1}{\sigma_1}-\rho \frac{y-\mu_2}{\sigma_2}, \\
v=\frac{y-\mu_2}{\sigma_2} \sqrt{1-\rho^2} .
\end{array}\right. { u = σ 1 x − μ 1 − ρ σ 2 y − μ 2 , v = σ 2 y − μ 2 1 − ρ 2 . 则可得
J − 1 = ∂ ( u , v ) ∂ ( x , y ) = ∣ 1 σ 1 − ρ σ 2 0 1 − ρ 2 σ 2 ∣ = 1 − ρ 2 σ 1 σ 2 , J^{-1}=\frac{\partial(u, v)}{\partial(x, y)}=\left|\begin{array}{cc}
\frac{1}{\sigma_1} & -\frac{\rho}{\sigma_2} \\
0 & \frac{\sqrt{1-\rho^2}}{\sigma_2}
\end{array}\right|=\frac{\sqrt{1-\rho^2}}{\sigma_1 \sigma_2}, J − 1 = ∂ ( x , y ) ∂ ( u , v ) = σ 1 1 0 − σ 2 ρ σ 2 1 − ρ 2 = σ 1 σ 2 1 − ρ 2 , 由此得
p = 1 2 π ( 1 − ρ 2 ) ∬ u 2 + v 2 ⩽ λ 2 exp { − u 2 + v 2 2 ( 1 − ρ 2 ) } d u d v . p=\frac{1}{2 \pi\left(1-\rho^2\right)} \iint_{u^2+v^2 \leqslant \lambda^2} \exp \left\{-\frac{u^2+v^2}{2\left(1-\rho^2\right)}\right\} d u d v . p = 2 π ( 1 − ρ 2 ) 1 ∬ u 2 + v 2 ⩽ λ 2 exp { − 2 ( 1 − ρ 2 ) u 2 + v 2 } d u d v . 再作极坐标变换
{ u = r sin α v = r cos α \left\{\begin{array}{l}
u=r \sin \alpha \\
v=r \cos \alpha
\end{array}\right. { u = r sin α v = r cos α 则可得
J − 1 = ∂ ( u , v ) ∂ ( r , α ) = ∣ sin α r cos α cos α − r sin α ∣ = − r ( sin 2 α + cos 2 α ) = − r , J^{-1}=\frac{\partial(u, v)}{\partial(r, \alpha)}=\left|\begin{array}{cc}
\sin \alpha & r \cos \alpha \\
\cos \alpha & -r \sin \alpha
\end{array}\right|=-r\left(\sin ^2 \alpha+\cos ^2 \alpha\right)=-r, J − 1 = ∂ ( r , α ) ∂ ( u , v ) = sin α cos α r cos α − r sin α = − r ( sin 2 α + cos 2 α ) = − r , 最后得
p = 1 2 π ( 1 − ρ 2 ) ∫ 0 2 π d α ∫ 0 λ r exp { − r 2 2 ( 1 − ρ 2 ) } d r = ∫ 0 1 exp { − r 2 2 ( 1 − ρ 2 ) } d ( r 2 2 ( 1 − ρ 2 ) ) = − exp { − r 2 2 ( 1 − ρ 2 ) } ∣ 0 1 = 1 − exp { − λ 2 2 ( 1 − ρ 2 ) } \begin{aligned}
p & =\frac{1}{2 \pi\left(1-\rho^2\right)} \int_0^{2 \pi} d \alpha \int_0^\lambda r \exp \left\{-\frac{r^2}{2\left(1-\rho^2\right)}\right\} d r \\
& =\int_0^1 \exp \left\{-\frac{r^2}{2\left(1-\rho^2\right)}\right\} d\left(\frac{r^2}{2\left(1-\rho^2\right)}\right) \\
& =-\left.\exp \left\{-\frac{r^2}{2\left(1-\rho^2\right)}\right\}\right|_0 ^1=1-\exp \left\{-\frac{\lambda^2}{2\left(1-\rho^2\right)}\right\}
\end{aligned} p = 2 π ( 1 − ρ 2 ) 1 ∫ 0 2 π d α ∫ 0 λ r exp { − 2 ( 1 − ρ 2 ) r 2 } d r = ∫ 0 1 exp { − 2 ( 1 − ρ 2 ) r 2 } d ( 2 ( 1 − ρ 2 ) r 2 ) = − exp { − 2 ( 1 − ρ 2 ) r 2 } 0 1 = 1 − exp { − 2 ( 1 − ρ 2 ) λ 2 } 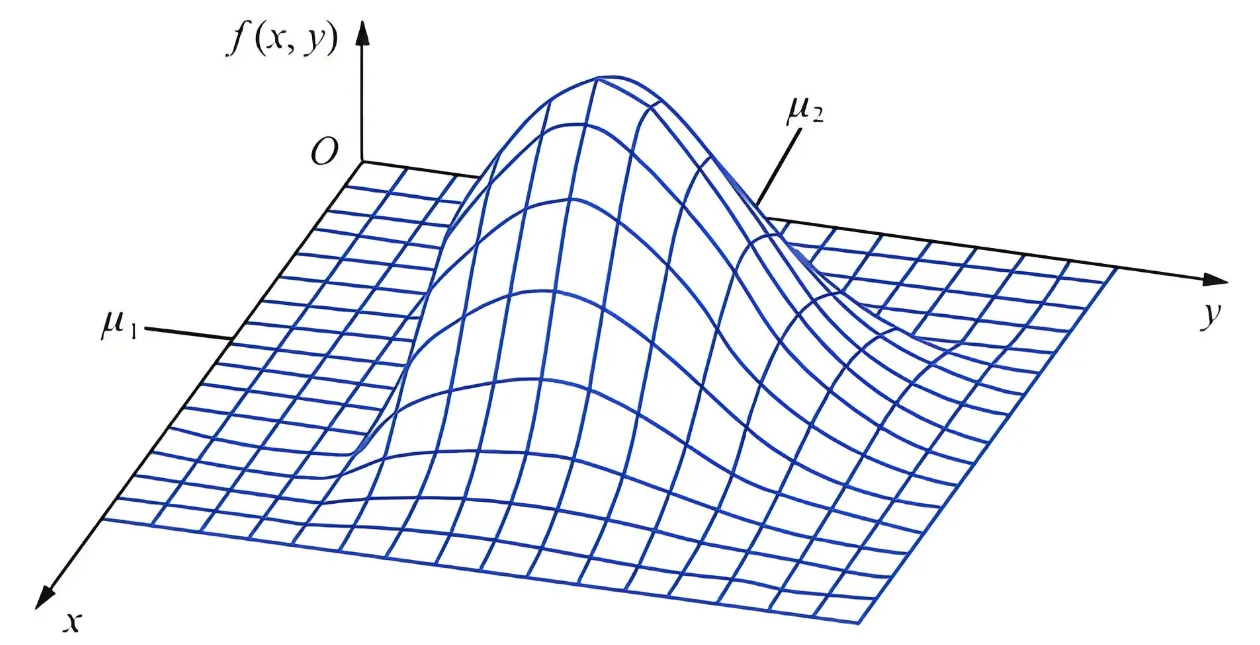
 。
利用极坐标变换,令 , 可得
。
利用极坐标变换,令 , 可得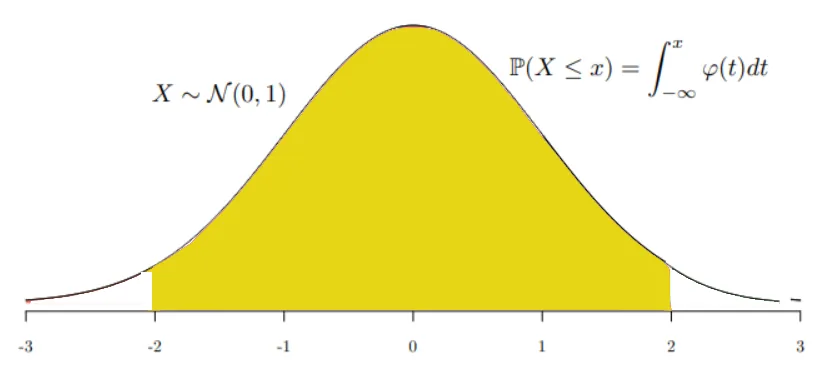 {width=600px}
{width=600px}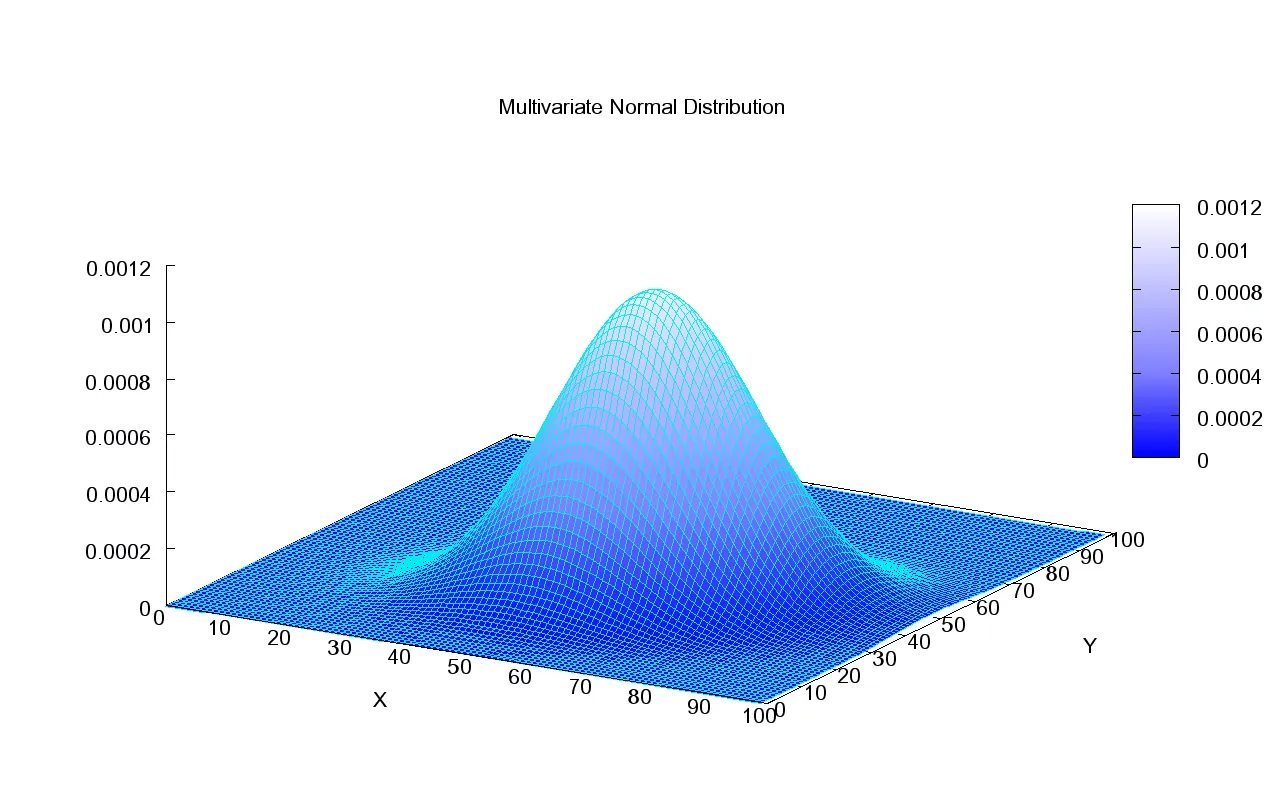 {width=600px}
{width=600px}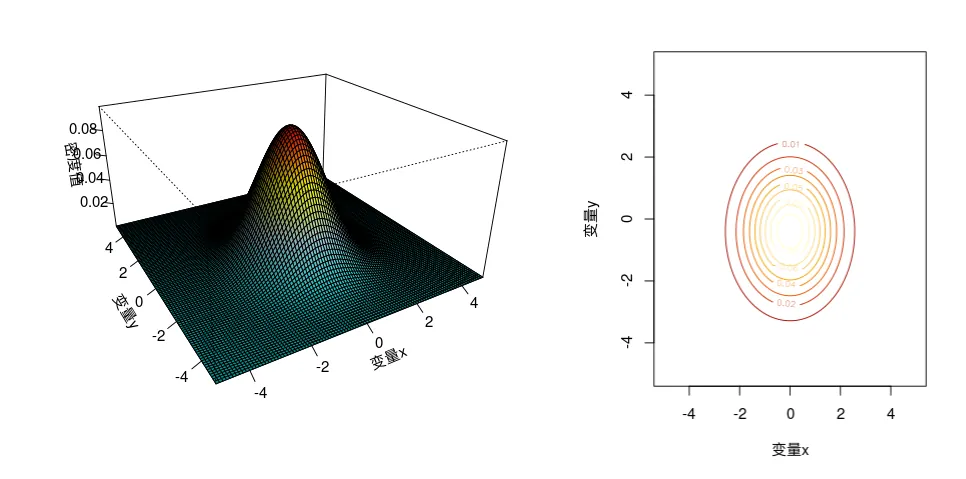 {width=800px}
{width=800px}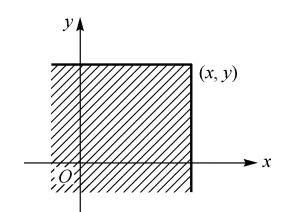
 {width=500px}
{width=500px}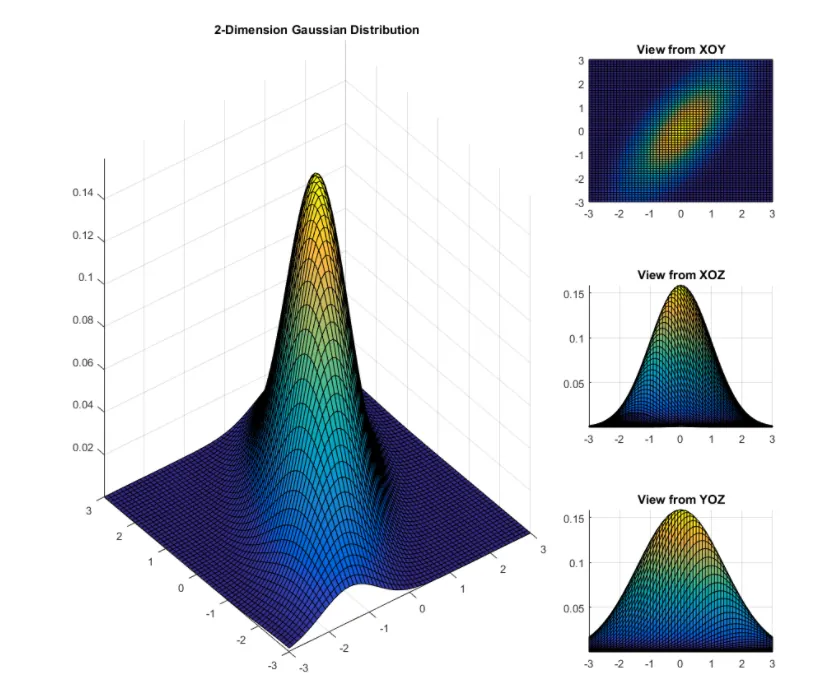 {width=500px}
{width=500px}