1._本章公式汇总

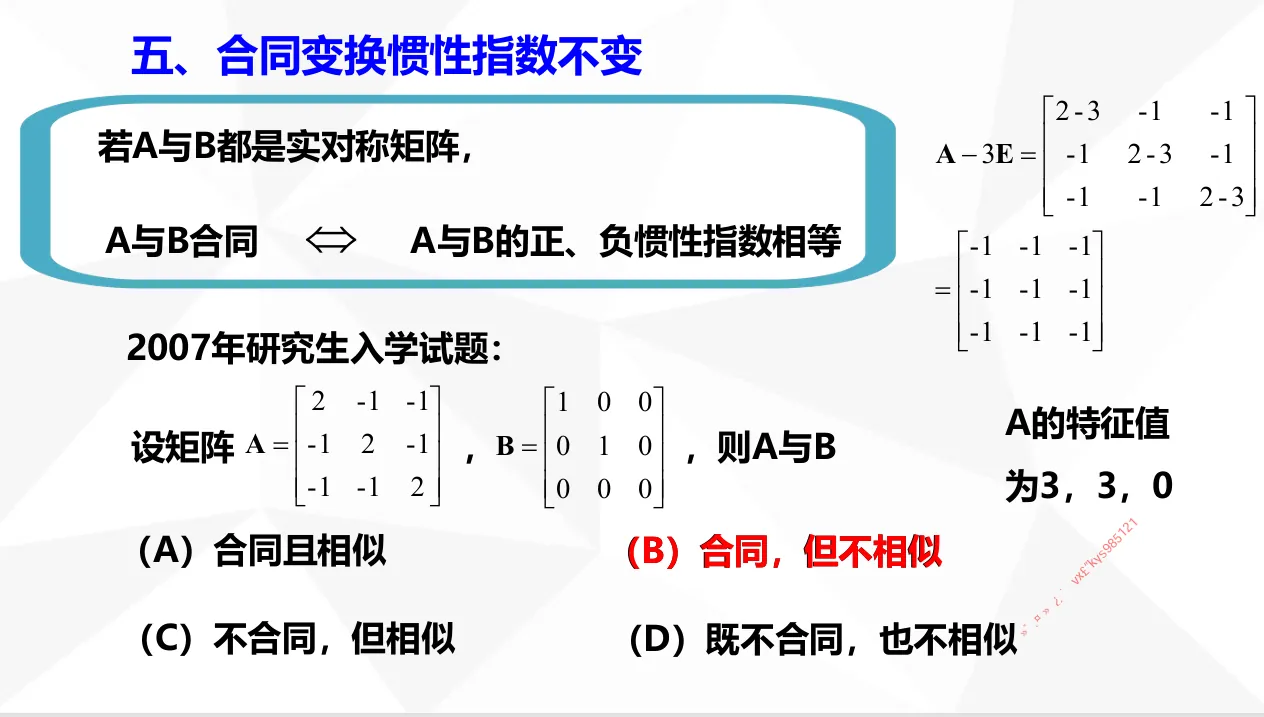
特征值与特征向量反应的是线性变换里的方向不变量，一个矩阵有3个线性无关的向量，相当于找到了三维空间里的新的坐标基，在这组基下观察几何体，更简介、漂亮。详见 为什么引入特征值与特征向量

本文摘自西安电子科技大学 B站 线帒杨 的共享资料。

线性代数化归思想

注①： 公式汇总主要参考 武忠祥 编制的 线性代数公式 注②： 图片汇总主要参考 西安电子科技大学教授杨威PPT，详见B站 线帒杨

特征值与特征向量的性质

(1) 设 $\lambda_1, \lambda_2, \cdots, \lambda_n$ 是 $n$ 阶方阵 $\boldsymbol{A}$ 的 $n$ 个特征值, 则 ①$\lambda_1+\lambda_2+\cdots+\lambda_n=a_{11}+a_{22}+\cdots+a_{n n}$. ② $\lambda_1 \lambda_2 \cdots \lambda_n=|\boldsymbol{A}|$.

公式释义：公式①反应和的不变性，即特征值之和等于主对角线元素的和，而②式反应的是积的不变性，即特征值之积为行列式的值。其实在 行列式 就介绍过，$n$阶行列式的值就是$n$个向量围成的体积，在特征向量坐标系，这个体积直接是对角线乘积。而和的值可以理解为距离，空间2个物体不管使用什么坐标系，尽管坐标值不懂，但是他们的距离是相同的。

(2) 矩阵 $\boldsymbol{A}$ 对应于不同特征值的特征向量线性无关. (3) 矩阵 $\boldsymbol{A}$ 的 $k$ 重特征值 $\lambda$ 至多有 $k$ 个线性无关的特征向量. 特别地, 当 $\boldsymbol{A}$ 有 $n$ 个 不同的特征值时 (没有重根), $\boldsymbol{A}$ 有 $n$ 个线性无关的特征向量. (4) 设 $n$ 阶方阵 $\boldsymbol{A}$ 的特征值为 $\lambda, \boldsymbol{A}$ 的属于特征值 $\lambda$ 的特征向量为 $\boldsymbol{\alpha}$, 则

相似矩阵的性质

$\boldsymbol{A}$ 与 $\boldsymbol{B}$ 相似 $\Rightarrow \boldsymbol{A}$ 与 $\boldsymbol{B}$ 有相同的特征多项式, 即 $|\boldsymbol{A}-\lambda \boldsymbol{E}|=|\boldsymbol{B}-\lambda \boldsymbol{E}|$

$\Rightarrow \boldsymbol{A}$ 与 $\boldsymbol{B}$ 有完全相同的特征值 (但是特征向量不一定相同)

$\Rightarrow|\boldsymbol{A}|=|\boldsymbol{B}|=\lambda_1 \lambda_2 \cdots \lambda_n, \quad \sum a_{i i}=\sum b_{i i}$

$\Rightarrow \boldsymbol{A}$ 与 $\boldsymbol{B}$ 等价, $\mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{B})$.

$\Rightarrow \boldsymbol{A}^{\mathrm{T}}$ 与 $\boldsymbol{B}^{\mathrm{T}}$ 相似, $\boldsymbol{A}^{-1}$ 与 $\boldsymbol{B}^{-1}$ 相似

$\Rightarrow f(A)$ 与 $f(B)$ 相似 ( $f$ 为多项式)

矩阵可相似对角化的条件

(1) $n$ 阶矩阵 $\boldsymbol{A}$ 可以对角化的充分必要条件是: $\boldsymbol{A}$ 有 $n$ 个线性无关的特征向量 (即 $\boldsymbol{A}$ 的 $k$ 重特征值 $\lambda$ 有 $k$ 个线性无关的特征向量）. (2) $n$ 阶矩阵 $\boldsymbol{A}$ 可以对角化的充分条件: ① $\boldsymbol{A}$ 有 $n$ 个不同的特征值, 则 $\boldsymbol{A}$ 一定能对角化. ② $\boldsymbol{A}$ 为实对称矩阵, 则 $\boldsymbol{A}$ 一定能对角化.

对角化的步骤

(1) 求出 $\boldsymbol{A}$ 的特征值 $\lambda_1, \lambda_2, \cdots, \lambda_n$;

(2) 求出 $\boldsymbol{A}$ 的 $n$ 个线性无关的特征向量 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n$;

(3) 令 $\boldsymbol{P}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n\right), \boldsymbol{A}=\left(\begin{array}{cccc}\lambda_1 & & & 0 \\ & \lambda_2 & & \\ & & \ddots & \\ 0 & & & \lambda_n\end{array}\right)$ , 则 $\boldsymbol{P}^{-1} \boldsymbol{A P}=\boldsymbol{A}$.

注意$\boldsymbol{\alpha_i}$的次序与$\lambda_i$的次序一定要一致

标准正交化

将一线性无关的向量组 (以 $\alpha_1, \alpha_2, \alpha_3$ 为例) 化为标准正交向量组的方法: 步骤 1. 施密特正交化:

步骤 2. 规范化（单位化):

用正交阵将对称阵对角化的步骤

(1) 求出对称阵 $\boldsymbol{A}$ 的特征值 $\lambda_1, \lambda_2, \cdots, \lambda_n$; (2) 求出 $\boldsymbol{A}$ 的 $n$ 个线性无关的特征向量 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n$; (3) 将 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n$ 正交化和单位化, 得到 $\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_n$; (4) 令 $\boldsymbol{Q}=\left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_n\right), \boldsymbol{\Lambda}=\left(\begin{array}{llll}\lambda_1 & & & 0 \\ & \lambda_2 & & \\ & & \ddots & \\ 0 & & & \lambda_n\end{array}\right)$, 则 $\boldsymbol{Q}^{-1} \boldsymbol{A} \boldsymbol{Q}=\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{Q}=\boldsymbol{\Lambda}$.