均匀分布是最简单的连续型分布,在数轴[a,b]之间随意点一个点,等待公交车时,等待的事件,都是连续型随机分布的经典例子。
均匀分布的密度函数和分布函数 前面曾以例子形式说明过均匀分布,这里给出一般的叙述:若随机变量 X X X
p ( x ) = { 1 b − a , a < x < b , 0 , 其他. p(x)= \begin{cases}\frac{1}{b-a}, & a<x<b, \\ 0, & \text { 其他. }\end{cases} p ( x ) = { b − a 1 , 0 , a < x < b , 其他 . 则称 X X X ( a , b ) (a, b) ( a , b ) X ∼ U ( a , b ) X \sim U(a, b) X ∼ U ( a , b )
均匀分布的密度函数如下图
均匀分布的分布函数 均匀分布的分布函数为
F ( x ) = { 0 , x < a , x − a b − a , a ⩽ x < b , 1 , x ⩾ b . F(x)= \begin{cases}0, & x<a, \\ \frac{x-a}{b-a}, & a \leqslant x<b, \\ 1, & x \geqslant b .\end{cases} F ( x ) = ⎩ ⎨ ⎧ 0 , b − a x − a , 1 , x < a , a ⩽ x < b , x ⩾ b . 如果从概率的角度理解,当x < a x<a x < a x > b x>b x > b
应用背景 均匀分布又被称为平顶分布, 它的背景可视作随机点 X X X ( a , b ) (a, b) ( a , b ) r r r X X X ( 0 , 2 π r ) (0,2 \pi r) ( 0 , 2 π r )
例 某公共汽车站从上午 7 时起,每 15 分钟来一班车,即 7 : 00 , 7 : 15 , 7 : 30 , 7 : 45 7: 00, ~ 7: 15, ~ 7: 30, ~ 7: 45 7 : 00 , 7 : 15 , 7 : 30 , 7 : 45 X X X
解 以 7:00 为起点 0 ,以分为单位,依题意
X ∼ U ( 0 , 30 ) , f ( x ) = { 1 30 , 0 < x < 30 0 , 其他 X \sim U(0,30), \quad f(x)= \begin{cases}\frac{1}{30}, & 0<x<30 \\ 0, & \text { 其他 }\end{cases} X ∼ U ( 0 , 30 ) , f ( x ) = { 30 1 , 0 , 0 < x < 30 其他 为使候车时间 X X X
P ( 10 < X < 15 ) + P ( 25 < X < 30 ) = ∫ 10 15 1 30 d x + ∫ 25 30 1 30 d x = 1 3 . P(10<X<15)+P(25<X<30)=\int_{10}^{15} \frac{1}{30} d x+\int_{25}^{30} \frac{1}{30} d x=\frac{1}{3} . P ( 10 < X < 15 ) + P ( 25 < X < 30 ) = ∫ 10 15 30 1 d x + ∫ 25 30 30 1 d x = 3 1 . 即乘客候车时间少于 5 分钟的概率是 1 / 3 1 / 3 1/3
均匀分布是概率统计中的一个重要分布,被广泛地应用于流行病学、遗传学、交通流量理论等概率模型中。
例 某食品厂生产一种产品,规定其质量的误差不能超过 3 g ,若随机误差 X X X ( − 3 , 3 ) (-3,3) ( − 3 , 3 ) − 1 ∼ 2 -1 \sim 2 − 1 ∼ 2 X ∼ U ( − 3 , 3 ) X \sim U(-3,3) X ∼ U ( − 3 , 3 )
f ( x ) = { 1 6 , − 3 < x < 3 , 0 , 其他. f(x)=\left\{\begin{array}{l}
\frac{1}{6},-3<x<3, \\
0, \text { 其他. }
\end{array}\right. f ( x ) = { 6 1 , − 3 < x < 3 , 0 , 其他 . 所求概率为 P { − 1 < X ⩽ 2 } = ∫ − 1 2 1 6 d x = 2 − ( − 1 ) 6 = 1 2 P\{-1<X \leqslant 2\}=\int_{-1}^2 \frac{1}{6} \mathrm{~d} x=\frac{2-(-1)}{6}=\frac{1}{2} P { − 1 < X ⩽ 2 } = ∫ − 1 2 6 1 d x = 6 2 − ( − 1 ) = 2 1
例设随机变量 X X X ( 1 , 4 ) (1,4) ( 1 , 4 ) X X X
解 随机变量 X X X
f ( x ) = { 1 3 , 1 < x < 4 , 0 , 其他. f(x)= \begin{cases}\frac{1}{3}, & 1<x<4, \\ 0, & \text { 其他. }\end{cases} f ( x ) = { 3 1 , 0 , 1 < x < 4 , 其他 . 所以,P { X > 2 } = ∫ 2 4 1 3 d x = 2 3 P\{X>2\}=\int_2^4 \frac{1}{3} \mathrm{~d} x=\frac{2}{3} P { X > 2 } = ∫ 2 4 3 1 d x = 3 2 Y Y Y Y ∼ B ( 3 , 2 3 ) Y \sim B\left(3, \frac{2}{3}\right) Y ∼ B ( 3 , 3 2 )
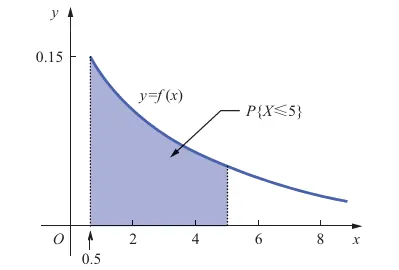
P { Y ⩾ 2 } = C 3 2 ( 2 3 ) 2 1 3 + C 3 3 ( 2 3 ) 3 ( 1 3 ) 0 = 20 27 . P\{Y \geqslant 2\}=\mathrm{C}_3^2\left(\frac{2}{3}\right)^2 \frac{1}{3}+\mathrm{C}_3^3\left(\frac{2}{3}\right)^3\left(\frac{1}{3}\right)^0=\frac{20}{27} . P { Y ⩾ 2 } = C 3 2 ( 3 2 ) 2 3 1 + C 3 3 ( 3 2 ) 3 ( 3 1 ) 0 = 27 20 . 例 车流中的"时间间隔"是指一辆车通过一个固定地点与下一辆车开始通过该固定地点之间的时间长度.设 X X X X X X
f ( x ) = { 0.15 e − 0.15 ( x − 0.5 ) , x ⩾ 0.5 , 0 , 其他. f(x)= \begin{cases}0.15 \mathrm{e}^{-0.15(x-0.5)}, & x \geqslant 0.5, \\ 0, & \text { 其他. }\end{cases} f ( x ) = { 0.15 e − 0.15 ( x − 0.5 ) , 0 , x ⩾ 0.5 , 其他 . 概率密度 f ( x ) f(x) f ( x )
解 由题意可得
P { X ⩽ 5 } = ∫ − ∞ 5 f ( x ) d x = ∫ 0.5 5 0.15 e − 0.15 ( x − 0.5 ) d x = 0.15 e 0.075 ∫ 0.5 5 e − 0.15 x d x = e 0.075 ( − e − 0.15 x ∣ 0.5 5 ) ≈ 0.491 \begin{aligned}
P\{X \leqslant 5\} & =\int_{-\infty}^5 f(x) \mathrm{d} x=\int_{0.5}^5 0.15 \mathrm{e}^{-0.15(x-0.5)} \mathrm{d} x \\
& =0.15 \mathrm{e}^{0.075} \int_{0.5}^5 \mathrm{e}^{-0.15 x} \mathrm{~d} x=\mathrm{e}^{0.075}\left(-\left.\mathrm{e}^{-0.15 x}\right|_{0.5} ^5\right) \\
& \approx 0.491
\end{aligned} P { X ⩽ 5 } = ∫ − ∞ 5 f ( x ) d x = ∫ 0.5 5 0.15 e − 0.15 ( x − 0.5 ) d x = 0.15 e 0.075 ∫ 0.5 5 e − 0.15 x d x = e 0.075 ( − e − 0.15 x 0.5 5 ) ≈ 0.491 均匀分布的数学期望与方差 设随机变量 X ∼ U ( a , b ) X \sim U(a, b) X ∼ U ( a , b )
E ( X ) = ∫ a b x b − a d x = b 2 − a 2 2 ( b − a ) = a + b 2 , E(X)=\int_a^b \frac{x}{b-a} d x=\frac{b^2-a^2}{2(b-a)}=\frac{a+b}{2}, E ( X ) = ∫ a b b − a x d x = 2 ( b − a ) b 2 − a 2 = 2 a + b , 这正是区间 ( a , b ) (a, b) ( a , b )
E ( X 2 ) = ∫ a b x 2 b − a d x = b 3 − a 3 3 ( b − a ) = a 2 + a b + b 2 3 , E\left(X^2\right)=\int_a^b \frac{x^2}{b-a} d x=\frac{b^3-a^3}{3(b-a)}=\frac{a^2+a b+b^2}{3}, E ( X 2 ) = ∫ a b b − a x 2 d x = 3 ( b − a ) b 3 − a 3 = 3 a 2 + ab + b 2 , 由此得 X X X
D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 = a 2 + a b + b 2 3 − ( a + b ) 2 4 = ( b − a ) 2 12 . D(X)=E\left(X^2\right)-[E(X)]^2=\frac{a^2+a b+b^2}{3}-\frac{(a+b)^2}{4}=\frac{(b-a)^2}{12} . D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 = 3 a 2 + ab + b 2 − 4 ( a + b ) 2 = 12 ( b − a ) 2 . 关于更多概率分布表见附录1:常见概率分布表
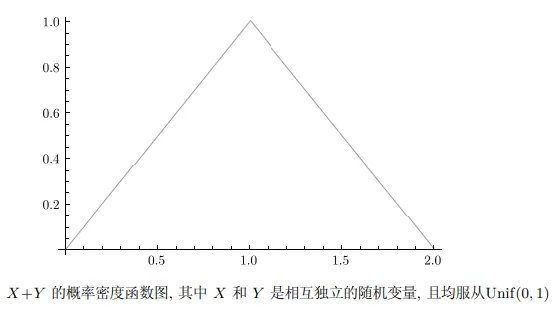
阅读:均匀分布之和的分布 关于服从均匀分布的随机变量,我们还有一个问题要回答:服从均匀分布的随机变量之和会服从什么样的分布呢?为了简单起见,不妨设 X X X Y Y Y [ 0 , 1 ] [0,1] [ 0 , 1 ]
设 X X X Y Y Y U ( 0 , 1 ) \operatorname{U}(0,1) U ( 0 , 1 ) Z = X + Y Z=X+Y Z = X + Y
f Z ( z ) = { z 若 0 ⩽ z ⩽ 1 2 − z 若 1 ⩽ z ⩽ 2 0 其他. \boxed{
f_Z(z)= \begin{cases}z & \text { 若 } 0 \leqslant z \leqslant 1 \\ 2-z & \text { 若 } 1 \leqslant z \leqslant 2 \\ 0 & \text { 其他. }\end{cases}
} f Z ( z ) = ⎩ ⎨ ⎧ z 2 − z 0 若 0 ⩽ z ⩽ 1 若 1 ⩽ z ⩽ 2 其他 . 利用卷积理论可以得出上述答案,即
f Z ( z ) = ∫ − ∞ ∞ f ( t ) f ( z − t ) d t , f ( u ) = { 1 若 0 ⩽ u ⩽ 1 0 其他. f_Z(z)=\int_{-\infty}^{\infty} f(t) f(z-t) d t, \quad f(u)= \begin{cases}1 & \text { 若 } 0 \leqslant u \leqslant 1 \\ 0 & \text { 其他. }\end{cases} f Z ( z ) = ∫ − ∞ ∞ f ( t ) f ( z − t ) d t , f ( u ) = { 1 0 若 0 ⩽ u ⩽ 1 其他 . 我们现在就来计算这个积分.不难想到,z z z z ⩽ 0 z \leqslant 0 z ⩽ 0 0 ⩽ z ⩽ 2 0 \leqslant z \leqslant 2 0 ⩽ z ⩽ 2 z ⩾ 2 z \geqslant 2 z ⩾ 2 [ 0 , 1 ] [0,1] [ 0 , 1 ] z ∈ [ 0 , 2 ] z \in[0,2] z ∈ [ 0 , 2 ] z ⩽ 0 z \leqslant 0 z ⩽ 0 z ⩾ 2 z \geqslant 2 z ⩾ 2 0 ⩽ z ⩽ 2 0 \leqslant z \leqslant 2 0 ⩽ z ⩽ 2
假设 z ⩽ 0 z \leqslant 0 z ⩽ 0 f ( t ) f ( z − t ) f(t) f(z-t) f ( t ) f ( z − t ) 0 ⩽ t ⩽ 1 0 \leqslant t \leqslant 1 0 ⩽ t ⩽ 1 0 ⩽ z − t ⩽ 1 0 \leqslant z-t \leqslant 1 0 ⩽ z − t ⩽ 1 z − 1 ⩽ t ⩽ z z-1 \leqslant t \leqslant z z − 1 ⩽ t ⩽ z z ⩽ 0 z \leqslant 0 z ⩽ 0 t ⩽ 0 t \leqslant 0 t ⩽ 0 z ⩽ 0 z \leqslant 0 z ⩽ 0 0 ⩽ z ⩽ 2 0 \leqslant z \leqslant 2 0 ⩽ z ⩽ 2 0 ⩽ t ⩽ 1 0 \leqslant t \leqslant 1 0 ⩽ t ⩽ 1 z − 1 ⩽ t ⩽ z z-1 \leqslant t \leqslant z z − 1 ⩽ t ⩽ z 0 ⩽ z ⩽ 2 0 \leqslant z \leqslant 2 0 ⩽ z ⩽ 2 z z z t t t z z z 0 ⩽ t ⩽ 1 0 \leqslant t \leqslant 1 0 ⩽ t ⩽ 1 0 ⩽ z ⩽ 1 0 \leqslant z \leqslant 1 0 ⩽ z ⩽ 1 z − 1 ⩽ 0 z-1 \leqslant 0 z − 1 ⩽ 0 z − 1 ⩽ t z-1 \leqslant t z − 1 ⩽ t t t t t ⩽ z t \leqslant z t ⩽ z z ⩾ 1 z \geqslant 1 z ⩾ 1 t ⩽ z t \leqslant z t ⩽ z z − 1 ⩽ t z-1 \leqslant t z − 1 ⩽ t
我们只考虑 0 ⩽ z ⩽ 1 0 \leqslant z \leqslant 1 0 ⩽ z ⩽ 1
总之,现在只需要考虑 0 ⩽ z ⩽ 1 0 \leqslant z \leqslant 1 0 ⩽ z ⩽ 1 0 ⩽ t ⩽ 1 0 \leqslant t \leqslant 1 0 ⩽ t ⩽ 1 z − 1 ⩽ t ⩽ z z-1 \leqslant t \leqslant z z − 1 ⩽ t ⩽ z t t t t ∈ [ 0 , 1 ] t \in[0,1] t ∈ [ 0 , 1 ] t ∈ [ 0 , z ] t \in[0, z] t ∈ [ 0 , z ] f ( t ) f ( z − t ) f(t) f(z-t) f ( t ) f ( z − t ) t t t t ∈ [ 0 , z ] t \in[0, z] t ∈ [ 0 , z ]
f Z ( z ) = ∫ 0 z 1 ⋅ 1 d t = z f_Z(z)=\int_0^z 1 \cdot 1 d t=z f Z ( z ) = ∫ 0 z 1 ⋅ 1 d t = z 正如前面所承诺的,我们简单地说一下,在不求积分的前提下,如何快速求出 z ⩾ 1 z \geqslant 1 z ⩾ 1 2 − z 2-z 2 − z X ~ = 1 − X \tilde{X}=1-X X ~ = 1 − X Y ~ = 1 − Y \tilde{Y}=1-Y Y ~ = 1 − Y X X X Y Y Y 1 / 2 1 / 2 1/2 X ~ \tilde{X} X ~ Y ~ \tilde{Y} Y ~ Unif ( 0 , 1 ) \operatorname{Unif}(0,1) Unif ( 0 , 1 ) X ~ + Y ~ ∈ [ 0 , 1 ] \tilde{X}+\tilde{Y} \in[0,1] X ~ + Y ~ ∈ [ 0 , 1 ] X + Y = 2 − ( X ~ + Y ~ ) ∈ [ 1 , 2 ] X+Y=2-(\tilde{X}+\tilde{Y}) \in[1,2] X + Y = 2 − ( X ~ + Y ~ ) ∈ [ 1 , 2 ] X ~ + Y ~ = u ∈ [ 0 , 1 ] \tilde{X}+\tilde{Y}=u \in[0,1] X ~ + Y ~ = u ∈ [ 0 , 1 ] u u u z ∈ [ 1 , 2 ] z \in[1,2] z ∈ [ 1 , 2 ] u u u u = 2 − z u=2-z u = 2 − z X + Y = Z X+Y=Z X + Y = Z 2 − z ! 2-z! 2 − z !
我们在图 中绘制了 X + Y X+Y X + Y ( X (X ( X Y Y Y U ( 0 , 1 ) ) \operatorname{U}(0,1)) U ( 0 , 1 ))
注意,结果是一个漂亮的三角形函数!如果回顾一下抛掷两颗均匀骰子得到的数字和,那么这个结果应该不会令人感到惊讶.在掷骰子的问题中,我们得到了一个三角形函数,"数字和为 7 "这一中间事件发生的概率是 6 / 36 6 / 36 6/36 1 / 36 1 / 36 1/36 r r r 6 − ∣ 7 − r ∣ 12 \frac{6-|7-r|}{12} 12 6 − ∣7 − r ∣
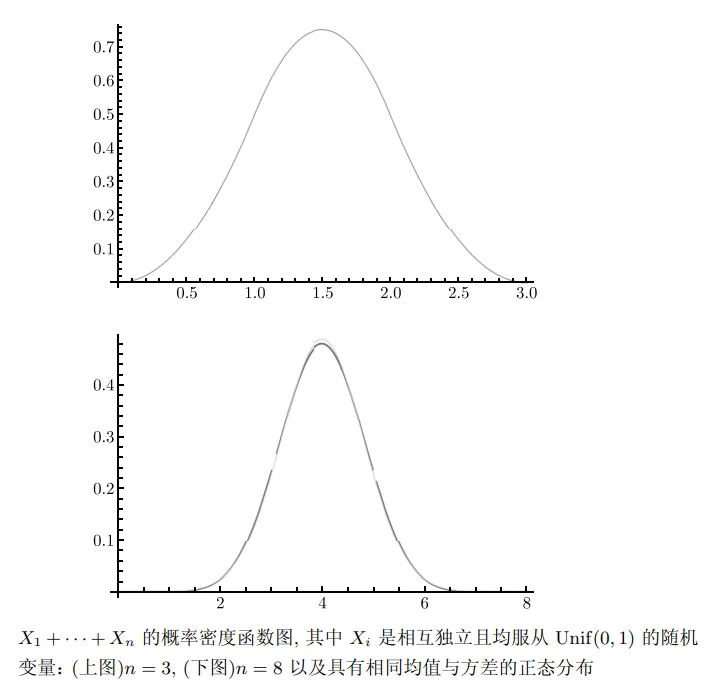
如果再次进行卷积会怎样呢?我们在图 13-2 中给出了答案,而且给出了 8 个相互独立且均服从 Unif ( 0 , 1 ) \operatorname{Unif}(0,1) Unif ( 0 , 1 )
概率论中最重要结果之一是,"好"的独立随机变量之和会收玫于正态分布.我们可以先看一下 8 个服从均匀分布的随机变量的情况,它与所对应的(具有相同均值与方差的)正态分布能够完美拟合!
对于任意多个独立且服从均匀分布的随机变量,我们可以明确写出它们的和的概率密度函数,但得到的概率密度函数仅是分段连续的,并且随着变量的不断累加,不同区域的数量也会增加.
{width=400px}
{width=400px}