15._连续型_正态分布-Part1 - 概率论与数理统计

引例1

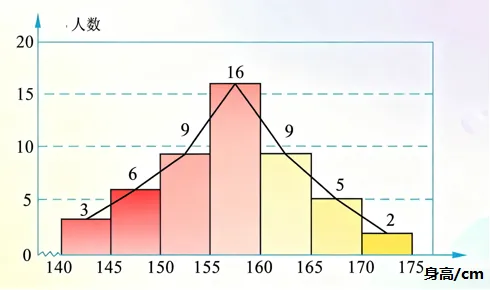
假设你的老妈担心你的单身生活，为此，在相亲网站给你寻找相亲对象，她把你的照片放到了相亲网站后，一下子吸引来了200多个女性留言，要与你"私定终身"。老妈为了提高篮选效率，于是乎就建了一个微信群，让所有人报一下自己准确的身高。为了统计方便。她以5厘米为单位，数一数每一段5厘米各有多少人。接着用身高为横轴，人数为纵轴，画了下面这张图。仔细看这张图，你和老妈发现一个惊人的秘密:这张图形状是中间高，两边低，长得像一只倒扣的钟。这意味着什么？意味着大部分女性身高在155-160cm之间，身高低于145cm或者高于170cm的都比较少。

$图片$ {width=400px}

引例2

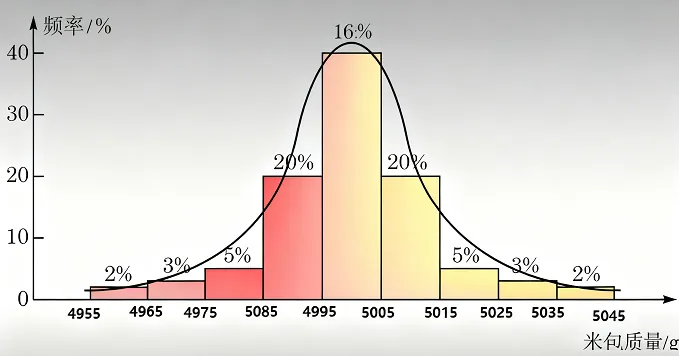
一包米的外包装上标示的质量是5000g，但实际上是有误差的，假设包装米的公司没有偷工减料，计量员精确地检测所有在售的该种米，把米包质量的频率分布直方图画出来，以10g为一组，绘出实际质量，会是一个什么形状呢？下图中是一条峰值在5000g左右的曲线，横坐标表示实际质量，纵坐标表示频率，可以发现它有一个单峰，长得也像一只倒扣的钟．也就是以5000g为中心，大部分质量都在5000g左右浮动，低于4955g和高于5045g的都很少。

$图片$ {width=400px}

从引例1和引例2可以看到，尽管问题环境不同，但是其结论类似。

正态分布

上面两个数据分布被称为正态分布，正态分布是概率论与数理统计中最重要的一个分布, 高斯 (Gauss, 1777-1855) 在研究误差理论时首先用正态分布来刻画误差的分布, 所以正态分布又称为高斯分布.

后续的中心极限定理表明:一个随机变量如果是由大量微小的、独立的随机因素的叠加结果, 那么这个变量一般都可以认为服从正态分布. 因此很多随机变量可以用正态分布描述或近似描述,世界上很多事物都符合正态分布曲线，大到金融、股市，小到心率、血压，考试成绩、身高等。甚至连超市入口停放的机动车都符合正态分布。

正态分布的密度函数

若随机变量 $X$ 的密度函数为

\varphi(x)=\dfrac{1}{\sqrt{2 \pi} \sigma} \mathrm{e}^{-\dfrac{(x-\mu)^2}{2 \sigma^2}}, \quad-\infty<x<\infty,

则称 $X$ 服从正态分布, 称 $X$ 为正态变量, 记作 $X \sim N\left(\mu, \sigma^2\right)$ . 其中参数 $-\infty<\mu<\infty, \sigma>0$ . 也就是他是一条连续的曲线。

初次接触正态分布的同学会感觉有点疑惑，传统的 $y=f(x)$ 都是一个变量，但是在正态分布里，有 $x,\mu,\sigma$ 三个参数。事实上现实生活里，女生找对象都要求“高富帅”，这里的“高富帅”就可以看成有三个参数。在正态函数里，为了了解 $f(x)$ 的图像特点，通常是先固定 $\mu$ 然后修改 $\sigma$ 看图形特点，然后固定 $\sigma$ 再修改 $\mu$ 再查看图像特点。

下图显示了正态分布的密度函数图像。 {width=500px}

为了研究正态函数图像特点，我们先固定 $\sigma$ 观察 $\mu$ 改变后函数图像的特点（下图左），和固定 $\mu$ 在更改 $\sigma$ 后函数图像的特点（下图右）

$图片$

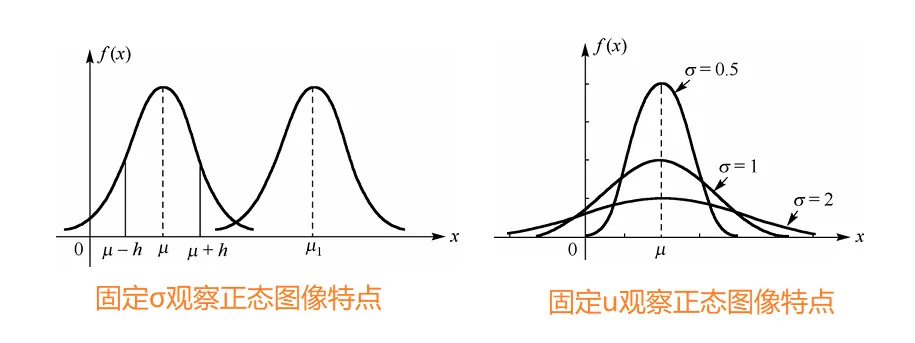
从图中可以得出一下结论：（1）正态分布的密度函数是左右关于 $x=\mu$ 对称， $\mu$ 是正态分布的中心，且在 $x=\mu$ 附近取值的可能性大, 在两侧取值的可能性小.

（2） $\mu \pm \sigma$ 是该曲线的拐点.

（3）假定 $\mu$ 固定，则 $\sigma$ 控制曲线的胖度。即 $\sigma$ 越大，曲线越胖， $\sigma$ 越小，曲线越瘦。

（4）后面可以证明，正态分布的数学期望 $E(X)=\mu$ , 方差为 $D(X)=\sigma ^2$

如果固定 $\sigma$ , 改变 $\mu$ 的值, 则图形沿 $x$ 轴平移, 而不改变其形状. 也就是说正态密度函数的位置由参数 $\mu$ 所确定, 因此亦称 $\mu$ 为位置参数.

如果固定 $\mu$ , 改变 $\sigma$ 的值, 则分布的位置不变, 但 $\sigma$ 愈小, 曲线呈高而瘦, 分布较为集中; $\sigma$ 愈大, 曲线呈矮而胖, 分布较为分散. 也就是说正态密度函数的尺度由参数 $\sigma$ 所确定, 因此称 $\sigma$ 为尺度参数（也叫为精度参数）. 具体理解可以参考本文最后一个例题理解。

正态分布的分布函数

正态分布 $N\left(\mu, \sigma^2\right)$ 的分布函数为

\Phi(X)=\frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^x \mathrm{e}^{-\frac{(t-\mu)^2}{2 \sigma^2}} \mathrm{~d} t .

它是一条光滑上升的 $S$ 形曲线, 见下图

{width=500px}

作为一个约定， $\varphi(x)$ 表示正态分布的密度函数， $\Phi(X)$ 表示正态分布的分布函数， $\varphi_0(x)$ 表示标准正态分布的密度函数， $\Phi_0(X)$ 表示标准正态分布的分布函数

标准正态分布

称 $\mu=0, \sigma=1$ 时的正态分布 $N(0,1)$ 为标准正态分布. 通常记标准正态变量为 $U$ , 记标准正态分布的密度函数为 $\varphi(u)$ , 分布函数为 $\Phi(u)$ , 即

\varphi(u)=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{u^2}{2}}, \quad-\infty<u<\infty,

\Phi(u)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^u \mathrm{e}^{-\frac{t^2}{2}} \mathrm{~d} t, \quad-\infty<u<\infty .

标准正态分布是有着非常优良的性质，具体会在下一节介绍。

正态分布的数学期望与方差

设随机变量 $X \sim N\left(\mu, \sigma^2\right)$ , 由于 $U=(X-\mu) / \sigma \sim N(0,1)$ , 所以 $U$ 的数学期望为

E(U)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} u e^{-\frac{U^2}{2}} d u,

注意到上述积分的被积函数为一个奇函数, 所以其积分值等于 0 , 即 $E(U)=0$ . 又因为 $X=\mu+\sigma U$ , 所以由数学期望的性质得

E(X)=\mu+\sigma \times 0=\mu .

也就是说, 正态分布 $N\left(\mu, \sigma^2\right)$ 中的 $\mu$ 为数学期望. 又因为

\begin{aligned} D(U) & =E\left(U^2\right)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} u^2 e^{-\frac{x^2}{2}} d u=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} u d\left(-e^{-\frac{\theta^2}{2}}\right) \\ & =\frac{1}{\sqrt{2 \pi}}\left(-\left.u e^{-\frac{u^2}{2}}\right|_{-\infty} ^{\infty}+\int_{-\infty}^{\infty} e^{-\frac{\Delta^2}{2}} d u\right)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} e^{-\frac{\omega^2}{2}} d u=\frac{1}{\sqrt{2 \pi}} \sqrt{2 \pi}=1, \end{aligned}

且 $X=\mu+\sigma U$ , 所以由方差的性质得

D(X)=D(\mu+\sigma U)=\sigma^2 .

这说明, 正态分布 $N\left(\mu, \sigma^2\right)$ 中另一个参数 $\sigma^2$ 就是 $X$ 的方差.

例 设某城市成年男子的身高 $X \sim N\left(170,6^2\right)$ （单位厘米）．问应如何设计公共汽车车门的高度，使成年男子与车门顶碰头的机会小于 0.01 ？

解：设车门高度为 $l$ 厘米，按设计要求应有 $P\{X>l\}<0.01$ ．由题设知 $X \sim N\left(170,6^2\right)$ ，将其标准化后有

\frac{X-170}{6} \sim N(0,1),

因此，按设计要求有

P\{X>l\}=1-P\{X \leqslant l\}=1-P\left\{\frac{X-170}{6} \leqslant \frac{l-170}{6}\right\}=1-\Phi\left(\frac{l-170}{6}\right)<0.01,

即 $\Phi\left(\frac{l-170}{6}\right)>0.99$ ，查表得 $\frac{l-170}{6}>2.33$ ，故

l>183.98 \text { (厘米). }

通过本题，我们再次理解一下，正态分布里， $\mu$ 和 $\sigma$ 的意义，这里的 $\mu$ 相当于平均身高， $\sigma$ 相当于身高误差。如果上面“设某城市成年男子的身高 $X \sim N\left(170,6^2\right)$ （单位厘米）” 这句话转换为通俗语言就是：某城市男生平均身高在170cm，其中大部分身高分布在 $164cm-176cm$ 。这样你大概理解 $\mu$ 和 $\sigma$ 的意义了。

这也就是为什么 $\mu$ 被称作位置参数， $\sigma$ 被称作尺度参数的原因了。