2._随机变量的定义

引言

为什么要引入随机变量？一句话：就是把试验结果数字化。

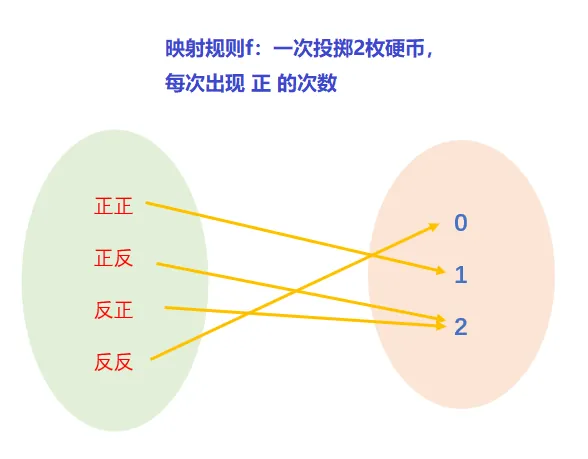
许多随机试验的结果与实数密切联系, 也有些随机试验结果从表面上看并不与实数相联系，但是我们可以通过映射让它与实数关联。 比如扔硬币，规定正面向上为1，反面向上为0，那么一次投掷两次硬币的结果就是： $\Omega=\{00,01,10,11\}$ 如果以$X$记正面向上的次数，那么上面样本空间里$00$表示两次反面朝上一共出现了$0$次，$01$和$10$表示一个正面朝上的次数，一共出现了2次可以用$2$表示，$11$表示两次正面朝上，一共出现了1次，可以用$1$表示，这样样本空间就可以写成 $X(\omega)=\{0,2,1\}$ 通过简单的“映射”，我们把试验的结果转换为了实数轴$R$上的函数。在这里就相当于把试验结果数字化了。

注意：这里的映射规则并不是唯一的，可以根据实际需求确定。

{width=400px}

再如公交车每隔5分钟来一次，那么一个人到公交车站台等车的时间就是 $\Omega=\{ 0 \leq x \leq 5 \}$ 可以直接把上面的等车时间映射为实数轴$R$上的函数 $X(\omega)=\{ 0 \leq x \leq 5 \}$

{width=400px}

在上面这两种映射里，这仅是映射的一种方式，就像扔硬币，你也可以映射“扔两次结果一样”的记做1，”扔两次结果不一样”的记做0，都是可以的，这不重要，重要的是他都可以映射为定义域为实数的函数。

通过上面2个例子，我们发现，随机事件可以用实数表示，为了弥补初等数学的缺陷，从整体上把握随机现象的统计规律，必须将随机试验的结果数量化，为此要引入随机变量．通过随机变量这个桥梁，可以把随机试验的结果与实数对应起来，建立一种映射关系，这样就能够使用高等数学的方法来研究随机试验，从而更充分地认识随机现象的统计规律

随机变量的另外一种类比理解就是字母处理，比如 用 0代表a,1代表b,2代表c，这样，abc 就可以表示成 012， 而cba就可以表示210.这样通过分析012三个数字之和和210三个数字之和（都为3）就可以推断abc和cba的关系

再如在一次民意调查中，我们调查 50 个人对某个事情的态度是支持（1）还是反对（0）。那么按照古典概型的处理方式，所有可能的结果有 $2^{50}$ 个，这是非常大的一个数字。但是如果我们用 $X=\{1$ 的个数 $\}$ ，则 $X$ 的可能取值为 $\{0,1, \cdots, 50\}$ ，这样处理起来就比原来的概率结构要方便多了．

下面我们在通过一个例子来引入随机变量的概念.

例题

例抛郑一颗均匀的股子，出现的点数的 样本空间取值 $=\{$ 正面朝上，反面朝上}, 样本空间不是一个数字集. 但是我们可以人为地把试验结果和实数对应起来.令 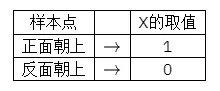这样，就可以把试验结果和实数集映射起来了，即 $\{X=1\}=\{$ 正面向上 $\},\{X=0\}=\{$ 反面向上 $\}$

这里也表明：一个随机变量是从样本空间 $\Omega$ 到实数轴的一个（映射）函数

随机变量的定义

在随机试验E中， $\Omega$ 是相应的样本空间，如果对 $\Omega$ 中的每一个样本点 $\omega$ ，有唯一一个实数 $X(\omega)$ 与它对应，那么就把这个定义域为 $\Omega$ 的单值实值函数$X=X(\omega)$ 称为是 (一维) 随机变量.

随机变量一般用大写字母 $X, Y, Z$ 表示. 引进随机变量后，随机事件及其概率可以通过随机变量来表达.

• 如果一个随机变量仅可能取有限或可列个值，则称其为离散型随机变量。

• 如果一个随机变量的取值充满了数轴上的一个区间（或某几个区间的并），则称其为连续型随机变量。

离散型随机变量：可能取值是可数有限个或可列无穷多个。 例如：火灾发生的次数、120电台电话被呼叫次数、骰子点数等

连续型随机变量：是指可能值可以连续的充满某个空间。 例如：灯泡的寿命、等车的时间等等。

如果从函数的角度看，简单的说，离散型的取值是整数，而连续型的取值是实数。

随机变量举例

随机变量$X$是样本点的函数，这个函数的自变量是样本点，可以是数，也可以不是数，定义域是样本空间，而因变量必须是实数。这个函数可以让不同的样本点对应不同的实数，也可以让多个样本点对应于一个实数。

例检查三个产品看看每个产品是否合格，每个产品有合格和不合格两种可能，这样三个产品就有8种可能，即有 8 个样本点, 若记 $X$ 为 “三个产品中的不合格品数”, 则 $X$的取值与样本点之间有如下对应关系:

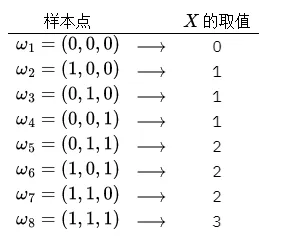
这样 $X$ 取各种值就是如下的的事件： $\{X=0\}=\left\{\omega_1\right\}$ $\{X=1\}=\left\{\omega_2, \omega_3, \omega_4\right\},$ $\{X=2\}=\left\{\omega_5, \omega_6, \omega_7\right\}$ $\{X=3\}=\left\{\omega_8\right\}$

有了随机变量，我们就可以知道，不合格超过1次的概率就是$P(X>1)$。

例在数轴上的有界区间 $[a, b]$ 上等可能地投点, 记 $X$ 为落点的位置（数轴上的坐标）， 因为等可能的投点在$[a,b]$区间，如果用$X$表示落点的位置，那么就可以直接把$X$映射为实数上的点。

注意：在概率论里通常是“约定大于配置”，比如我们常用大写字母如 $X, Y, Z, W, \cdots$ 表示随机变量, 而用小写字母如 $x, y, z, w, \cdots$ 表示其取值.当描述一个随机变量时, 不仅要说明它能够取哪些值, 而且还要指出它取这些值的概率。只有这样，才能真正完整地刻画一个随机变量。

再论为什么引入随机变量的概念

关于随机变量（及向量）的研究，是概率论的中心内容。这是因为，对于一个随机试验，我们所关心的往往是与所研究的特定问题有关的某个或某些量，而这些量就是随机变量。当然，有时我们所关心的是某个或某些特定的随机事件。

例如，在特定一群人中，年收入十万元以上的高收入者, 年收入在 3000 元以下的低收入者，各自的比率如何，这看上去像是两个孤立的事件。可是，若我们引进一个随机变量的 $X=$ {随机抽出一个人其年收入} 则 $X$ 是我们关心的随机变量.

上述两个事件可分别表为 $\{X > 100000\}$ 和 $\{X<3000\}$. 这就看出: 随机事件这个概念实际上是包容在随机变量这个更广的概念之内. 也可以说：随机事件是从静态的观点来研究随机现象, 而随机变量则是一种动态的观点, 一如数学分析中的常量与变量的区分那样。变量概念是高等数学有别于初等数学的基础概念. 同样, 概率论能从计算一些孤立事件的概念发展为一个更高的理论体系,其基础概念是随机变量.