假设检验的背景 在实际问题中,假设检验有着广泛的应用,请看三个引例。
引例1 某洗衣粉厂用自动包装机进行包装,正常情况下包装质量 (单位:g g g X ∼ N ( 500 , 9 ) X \sim N(500,9) X ∼ N ( 500 , 9 ) x ˉ = \bar{x}= x ˉ = μ \mu μ
这个问题实际上是根据理论分析,要求在 μ = 500 \mu=500 μ = 500 μ ≠ 500 \mu \neq 500 μ = 500 μ = 500 \mu=500 μ = 500 μ ≠ \mu \neq μ =
引例2 设有某车间生产的甲、乙两批同型号的产品,其次品率分别为 p 1 p_1 p 1 p 2 p_2 p 2 p 1 p_1 p 1 p 2 p_2 p 2 p 1 < p 2 p_1<p_2 p 1 < p 2
此例是要求在 p 1 < p 2 p_1<p_2 p 1 < p 2 p 1 ⩾ p 2 p_1 \geqslant p_2 p 1 ⩾ p 2 p 1 < p 2 p_1 <p_2 p 1 < p 2
引例3 将一枚骰子随机地掷 120 次,并统计出各点数出现的次数如下
问这枚骰子的六个面是否均匀?
这里检验的对象是该骰子的六个面均匀或不均匀,如果该骰子的六个面是均匀的,则意味着任意掷一次骰子所出现的点数X应具有下列分布律
因此,此例实际上是对X所服从的分布进行检验
总结
以上三个例子均为假设检验问题,由此可见,假设检验问题是非常丰富多样的。按检验的内容,假设检验可分为参数检验 和非参数检验
如果总体X的分布类型已知,检验只涉及其中的某些参数,这类假设检验称为参数检验如引例1中,已知包装量X服从正态分布,检验μ = 500 \mu=500 μ = 500 μ ≠ 500 \mu \ne 500 μ = 500
X = { 0 , 如果从甲批产品中任取一个产品为正品, 1 , 如果从甲批产品中任取一个产品为次品, X=\left\{\begin{array}{l}0, \text { 如果从甲批产品中任取一个产品为正品,} \\ 1, \text { 如果从甲批产品中任取一个产品为次品,}\end{array}\right. X = { 0 , 如果从甲批产品中任取一个产品为正品, 1 , 如果从甲批产品中任取一个产品为次品,
Y = { 0 , 如果从乙批产品中任取一个产品为正品, 1 , 如果从乙批产品中任取一个产品为次品, Y=\left\{\begin{array}{l}0, \text { 如果从乙批产品中任取一个产品为正品,} \\ 1, \text { 如果从乙批产品中任取一个产品为次品,}\end{array}\right. Y = { 0 , 如果从乙批产品中任取一个产品为正品, 1 , 如果从乙批产品中任取一个产品为次品, X ∼ B ( 1 , p 1 ) , Y ∼ B ( 1 , p 2 ) X \sim B\left(1, p_1\right), ~ Y \sim B\left(1, p_2\right) X ∼ B ( 1 , p 1 ) , Y ∼ B ( 1 , p 2 ) X X X Y Y Y p 1 < p 2 p_1<p_2 p 1 < p 2 p 1 ⩾ p 2 p_1 \geqslant p_2 p 1 ⩾ p 2
如果检验问题涉及总体X的分布类型(其中可以包含总体未知参数),而不只是未知参数,这类检验为非参数检验,如引例3中的检验问题就属于非参数检验问题
本篇主要介绍参数检验的思想和方法
在参数检验问题中,又会出现单总体和多总体情形.如例1为单总体情形,例2为双总体情形.另外,在参数检验问题中,根据实际需要,还会出现双边检验和单边检验。如例1为双边检验;例2为单边检验.
由上不难发现,假设检验不同于参数估计.参数估计是想了解总体 X X X θ \theta θ θ \theta θ θ \theta θ μ = 500 \mu=500 μ = 500 μ ≠ 500 \mu \neq 500 μ = 500 μ ≠ 500 \mu \neq 500 μ = 500 μ \mu μ p 1 < p 2 p_1<p_2 p 1 < p 2 p 1 ⩾ p 2 p_1 \geqslant p_2 p 1 ⩾ p 2 p 1 p_1 p 1 p 2 p_2 p 2
由于样本的随机性,我们不能简单直观地对检验问题作出回答 .比如在例2中, 36 件甲批产品中的次品率为 2 36 ≈ 5.56 % , 50 \frac{2}{36} \approx 5.56 \%, 50 36 2 ≈ 5.56% , 50 3 50 = 6 % \frac{3}{50}=6 \% 50 3 = 6% 5.56 % < 6 % 5.56 \%<6 \% 5.56% < 6% p 1 < p 2 p_1< p_2 p 1 < p 2
假设的提法 称检验问题中相互对立的两个命题为假设 或统计假设,并将其中一个命题称为原假设 或零假设 ,记为H 0 H_0 H 0 备择假设 或对立假设 ,记为H 1 H_1 H 1 ( H 0 , H 1 ) (H_0,H_1) ( H 0 , H 1 ) μ = 500 \mu=500 μ = 500 H 0 : μ = 500 H_0: \mu=500 H 0 : μ = 500 μ ≠ 500 \mu \neq 500 μ = 500 H 1 : μ ≠ H_1: \mu \neq H 1 : μ =
H 0 : μ = 500 , H 1 : μ ≠ 500 H_0: \mu=500, \quad H_1: \mu \neq 500 H 0 : μ = 500 , H 1 : μ = 500 在例2中,p 1 < p 2 p_1<p_2 p 1 < p 2 H 1 : p 1 < p 2 H_1: p_1< p_2 H 1 : p 1 < p 2 H 0 : p 1 ⩾ p 2 H_0: p_1 \geqslant p_2 H 0 : p 1 ⩾ p 2 H 0 : p 1 ⩾ p 2 H_0: p_1 \geqslant p_2 H 0 : p 1 ⩾ p 2 H 0 ′ : p 1 = p 2 H_0^{\prime}: p_1=p_2 H 0 ′ : p 1 = p 2 H 1 H_1 H 1 p 1 < p 2 p_1<p_2 p 1 < p 2 H 1 ′ : p 1 ≠ p 2 H_1^{\prime}: p_1 \neq p_2 H 1 ′ : p 1 = p 2 H 1 ′ H_1^{\prime} H 1 ′ p 1 > p 2 p_1>p_2 p 1 > p 2
H 0 : p 1 ⩾ p 2 , H 1 : p 1 < p 2 , 或 H 0 ′ : p 1 = p 2 , H 1 : p 1 < p 2 . H_0: p_1 \geqslant p_2, H_1: p_1<p_2 \text {, 或 } H_0^{\prime}: p_1=p_2, H_1: p_1<p_2 \text {. } H 0 : p 1 ⩾ p 2 , H 1 : p 1 < p 2 , 或 H 0 ′ : p 1 = p 2 , H 1 : p 1 < p 2 . 同理,例3的假设检验问题为
H 0 H_0 H 0 H 1 H_1 H 1
假设检验的思想和方法 1.假设检验中的反证法思想 在数学中,证明某命题成立时,经常运用反证法,即先假定该命题不成立,然后进行理论分析和演算,得到矛盾的结果,表明"假定该命题不成立"是错误的,从而证明了该命题成立.
在假设检验问题 ( H 0 , H 1 ) \left(H_0, H_1\right) ( H 0 , H 1 ) H 0 H_0 H 0 H 0 H_0 H 0 H 1 H_1 H 1 H 0 H_0 H 0 H 0 H_0 H 0 H 1 H_1 H 1
现在的问题是,如何正确理解和认识上述"矛盾"的现象".事实上,这里的"矛盾"并不是指真正意义上与已有条件相抵触的"矛盾".所谓 "‘矛盾’的现象",实际上是指某种"不正常的现象",这与假设检验的基本原理有着密切的关系。
2.假设检嬐的基本原理 先介绍小概率原理,即在正常情况下,小概率事件在一次抽样中是几乎不可能发生的 .
反之,如果在一次抽样中,某小概率事件 A A A H 0 , H 1 H_0, H_1 H 0 , H 1 H 0 H_0 H 0 H 0 H_0 H 0 H 1 H_1 H 1
下面举例说明假设检验的基本原理.
例某食品厂生产的罐头质量(单位: g )X ∼ N ( μ , 4 ) X \sim N(\mu, 4) X ∼ N ( μ , 4 ) μ = 500 \mu=500 μ = 500 x ˉ = 502 g \bar{x}=502 \mathrm{~g} x ˉ = 502 g μ = 500 \mu=500 μ = 500
解 由题意知,本题的假设检验问题为 H 0 : μ = 500 , H 1 : μ ≠ 500 H_0: \mu=500, H_1: \mu \neq 500 H 0 : μ = 500 , H 1 : μ = 500 H 0 H_0 H 0 μ = 500 \mu=500 μ = 500 μ \mu μ μ \mu μ 正态总体的抽样分布
知,U = X ˉ − μ σ / n = 当 H 0 成立时 X ˉ − 500 σ / n ∼ N ( 0 , 1 ) U=\frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \xlongequal{\text { 当 } H_0 \text { 成立时 }} \frac{\bar{X}-500}{\sigma / \sqrt{n}} \sim N(0,1) U = σ / n X ˉ − μ 当 H 0 成立时 σ / n X ˉ − 500 ∼ N ( 0 , 1 ) σ = 2 , n = 16 , x ˉ = 502 \sigma=2, n=16, \bar{x}=502 σ = 2 , n = 16 , x ˉ = 502
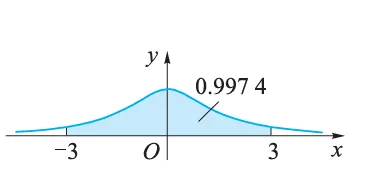
u 0 = 502 − 500 2 / 16 = 4. u_0=\frac{502-500}{2 / \sqrt{16}}=4 . u 0 = 2/ 16 502 − 500 = 4. 由于 U ∼ N ( 0 , 1 ) U \sim N(0,1) U ∼ N ( 0 , 1 ) 3 σ 3 \sigma 3 σ P { ∣ U ∣ < 3 } = P\{|U|<3\}= P { ∣ U ∣ < 3 } = ,从而 ,从而 ,从而 ,表明 ,表明 ,表明 的取值基本上都落在区间 的取值基本上都落在区间 的取值基本上都落在区间 内(如图),而在其外的可能性很小,因此事件 内(如图),而在其外的可能性很小,因此事件 内(如图),而在其外的可能性很小,因此事件
现在已经求得 u 0 = 4 u_0=4 u 0 = 4 A = { ∣ U ∣ ⩾ 3 } A=\{|U| \geqslant 3\} A = { ∣ U ∣ ⩾ 3 } H 0 H_0 H 0 μ = 500 \mu=500 μ = 500
例1只是用来介绍假设检验的基本原理,其中还有许多问题并没有讲透.比如,为什么选择统计量为 U = X ˉ − 500 σ / n U=\frac{\bar{X}-500}{\sigma / \sqrt{n}} U = σ / n X ˉ − 500 A = { ∣ U ∣ ⩾ 3 } A=\{|U| \geqslant 3\} A = { ∣ U ∣ ⩾ 3 } 3 σ 3 \sigma 3 σ χ 2 \chi^2 χ 2 t t t F F F A A A
假设检验的两类错误 根据假设检验的基本原理知道,在假定 H 0 H_0 H 0 g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n ) g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n ) A A A ( x 1 , x 2 , ⋯ , x n ) \left(x_1, x_2, \cdots, x_n\right) ( x 1 , x 2 , ⋯ , x n ) g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n ) g ( x 1 , x 2 , ⋯ , x n ) g\left(x_1, x_2, \cdots, x_n\right) g ( x 1 , x 2 , ⋯ , x n ) g ( x 1 , x 2 , ⋯ , x n ) g\left(x_1, x_2, \cdots, x_n\right) g ( x 1 , x 2 , ⋯ , x n ) A A A ( H 0 , H 1 ) \left(H_0, H_1\right) ( H 0 , H 1 )
如果小概率事件 A A A H 0 H_0 H 0 A A A g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n ) H 0 H_0 H 0 拒绝域 ,记为 W W W A A A H 0 H_0 H 0 A A A g ( X 1 g\left(X_1\right. g ( X 1 X 2 , ⋯ , X n ) \left.X_2, \cdots, X_n\right) X 2 , ⋯ , X n ) H 0 H_0 H 0 接受域 .
由于样本具有随机性,在一次抽样中,A A A
(1)真实情况 $H_0$ 成立,且检验结果接受 $H_0$ ,拒绝 $H_1$ ;
(2)真实情况 $H_0$ 成立,而检验结果拒绝 $H_0$ ,接受 $H_1$ ;
(3)真实情况 $H_1$ 成立,而检验结果接受 $H_0$ ,拒绝 $H_1$ ;
(4)真实情况 $H_1$ 成立,且检验结果拒绝 $H_0$ ,接受 $H_1$ 。由此可见,其中(1)和(4)中的检验结果与真实情况完全吻合,表明理论判断正确.但(2)和(3)中两者不一致,表明理论判断有误,这就是假设检验的两类错误.
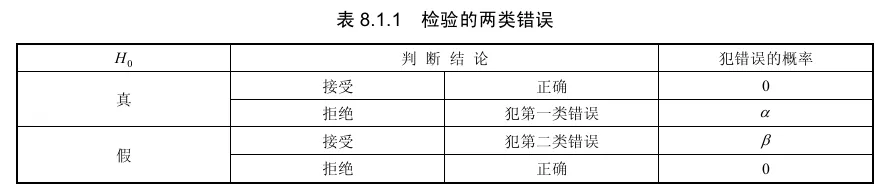
两类错误 定义 称真实情况 H 0 H_0 H 0 H 0 H_0 H 0 第一类错误 或弃真错误 ;
称真实情况 H 1 H_1 H 1 H 0 H_0 H 0 第二类错误 或存伪错误 。
上述假设检验的两类错误见下表.
由此可知,检验结果无论是接受 H 0 H_0 H 0 H 1 H_1 H 1
记犯第一类错误即弃真错误的概率为 α \alpha α β \beta β n n n α \alpha α β \beta β n n n α \alpha α β \beta β α \alpha α β \beta β
由于犯第一类错误时,检验出本来不存在的现象 H 1 H_1 H 1 犯第一类错误的危害性比犯第二类错误的危害性要大 。同时也兼顾到假设检验的原理、思想和方法,所以目前比较流行的做法是采用"优先固定或限制犯第一类错误概率 α \alpha α α \alpha α 0.05 , 0.01 0.05,0.01 0.05 , 0.01 α = 0.05 \alpha=0.05 α = 0.05
当小概率事件 A A A H 0 H_0 H 0 H 1 H_1 H 1 H 1 H_1 H 1 α ⩽ P ( A ) \alpha \leqslant P(A) α ⩽ P ( A ) H 0 H_0 H 0 α = P ( A ) \alpha=P(A) α = P ( A ) A A A P ( A ) = α P(A)=\alpha P ( A ) = α
在优先固定或限制犯第一类错误概率 α \alpha α β \beta β n n n β \beta β 正态抽样 统计量,就能使得在固定或限制犯第一类错误概率 α \alpha α β \beta β β \beta β U = X ˉ − 500 σ / n ∼ N ( 0 , 1 ) U=\frac{\bar{X}-500}{\sigma / \sqrt{n}} \sim N(0,1) U = σ / n X ˉ − 500 ∼ N ( 0 , 1 )
显著性检验 假设检验中有一个特点是量变可能引起质变,也就是说量变到一定的程度就不是"简单的量变",而是产生、本质上的变化(总体的状况已经发生变化)。
例如,在购买白糖时,每袋白糖标准质量为 500 g ,现任意购买了 1 袋白糖,测得其质量为 499 g ,虽然 499 < 500 499<500 499 < 500
显著性检验指的是对于检验问题 ( H 0 , H 1 ) \left(H_0, H_1\right) ( H 0 , H 1 ) H 0 H_0 H 0 H 0 H_0 H 0
根据假设检验的基本原理,先假定 H 0 H_0 H 0 g ( X 1 g\left(X_1\right. g ( X 1 X 2 , ⋯ , X n ) \left.X_2, \cdots, X_n\right) X 2 , ⋯ , X n ) ( x 1 , x 2 , ⋯ , x n ) \left(x_1, x_2, \cdots, x_n\right) ( x 1 , x 2 , ⋯ , x n ) g ( x 1 , x 2 , ⋯ , x n ) g\left(x_1, x_2, \cdots, x_n\right) g ( x 1 , x 2 , ⋯ , x n ) g ( x 1 , x 2 , ⋯ , x n ) g\left(x_1, x_2, \cdots, x_n\right) g ( x 1 , x 2 , ⋯ , x n ) H 0 H_0 H 0 H 0 H_0 H 0 犯第一类错误的概率 α \alpha α .
显著性水平 α \alpha α g ( x 1 , x 2 , ⋯ , x n ) g\left(x_1, x_2, \cdots, x_n\right) g ( x 1 , x 2 , ⋯ , x n )
通俗地讲,显著性水平 α \alpha α g ( x 1 , x 2 , ⋯ , x n ) g\left(x_1, x_2, \cdots, x_n\right) g ( x 1 , x 2 , ⋯ , x n ) H 0 H_0 H 0 H 0 H_0 H 0 H 0 H_0 H 0 α \alpha α H 0 H_0 H 0 W W W
P { g ( X 1 , X 2 , ⋯ , X n ) ∈ W } = P ( A ) = α P\left\{g\left(X_1, X_2, \cdots, X_n\right) \in W\right\}=P(A)=\alpha P { g ( X 1 , X 2 , ⋯ , X n ) ∈ W } = P ( A ) = α 因此,前面所提及的小概率事件 A A A
A = { g ( X 1 , X 2 , ⋯ , X n ) ∈ W } A=\left\{g\left(X_1, X_2, \cdots, X_n\right) \in W\right\} A = { g ( X 1 , X 2 , ⋯ , X n ) ∈ W } 现在的问题是如何确定 H 0 H_0 H 0 W W W H 0 H_0 H 0 W W W g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n )
双侧检验与单侧检验 定义 如果假设检验问题 ( H 0 , H 1 ) \left(H_0, H_1\right) ( H 0 , H 1 ) H 0 : θ = θ 0 , H 1 : θ ≠ θ 0 H_0: \theta=\theta_0, H_1: \theta \neq \theta_0 H 0 : θ = θ 0 , H 1 : θ = θ 0
如果假设检验问题 ( H 0 , H 1 ) \left(H_0, H_1\right) ( H 0 , H 1 ) H 0 : θ ⩾ θ 0 , H 1 : θ < θ 0 H_0: \theta \geqslant \theta_0, H_1: \theta<\theta_0 H 0 : θ ⩾ θ 0 , H 1 : θ < θ 0 H 0 : θ ⩽ θ 0 , H 1 : θ > θ 0 H_0: \theta \leqslant \theta_0, H_1: \theta>\theta_0 H 0 : θ ⩽ θ 0 , H 1 : θ > θ 0
对于双侧检验,由显著性水平 α \alpha α g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n ) g α 2 g_{\frac{\alpha}{2}} g 2 α g 1 − α 2 g_{1-\frac{\alpha}{2}} g 1 − 2 α H 0 H_0 H 0
W = { g ( X 1 , X 2 , ⋯ , X n ) ⩽ g 1 − α 2 或 g ( X 1 , X 2 , ⋯ , X n ) ⩾ g α 2 } , W=\left\{g\left(X_1, X_2, \cdots, X_n\right) \leqslant g_{1-\frac{\alpha}{2}} \quad \text { 或 } \quad g\left(X_1, X_2, \cdots, X_n\right) \geqslant g_{\frac{\alpha}{2}}\right\} \text {, } W = { g ( X 1 , X 2 , ⋯ , X n ) ⩽ g 1 − 2 α 或 g ( X 1 , X 2 , ⋯ , X n ) ⩾ g 2 α } , 其中 g α 2 g_{\frac{\alpha}{2}} g 2 α g 1 − α 2 g_{1-\frac{\alpha}{2}} g 1 − 2 α P { g ( X 1 , X 2 , ⋯ , X n ) ⩽ g 1 − α 2 } = P { g ( X 1 , X 2 , ⋯ , X n ) ⩾ P\left\{g\left(X_1, X_2, \cdots, X_n\right) \leqslant g_{1-\frac{\alpha}{2}}\right\}=P\left\{g\left(X_1, X_2, \cdots, X_n\right) \geqslant\right. P { g ( X 1 , X 2 , ⋯ , X n ) ⩽ g 1 − 2 α } = P { g ( X 1 , X 2 , ⋯ , X n ) ⩾
g α 2 } = α 2 \left.g_{\frac{\alpha}{2}}\right\}=\frac{\alpha}{2} g 2 α } = 2 α 对于单侧检验,理论上已经证明,H 0 : θ ⩾ θ 0 , H 1 : θ < θ 0 H_0: \theta \geqslant \theta_0, H_1: \theta<\theta_0 H 0 : θ ⩾ θ 0 , H 1 : θ < θ 0 H 0 : θ = θ 0 , H 1 : θ < θ 0 ; H 0 : θ ⩽ θ 0 , H 1 : θ > θ 0 H_0: \theta= \theta_0, H_1: \theta<\theta_0 ; H_0: \theta \leqslant \theta_0, H_1: \theta>\theta_0 H 0 : θ = θ 0 , H 1 : θ < θ 0 ; H 0 : θ ⩽ θ 0 , H 1 : θ > θ 0 H 0 : θ = θ 0 , H 1 : θ > θ 0 H_0: \theta=\theta_0, H_1: \theta>\theta_0 H 0 : θ = θ 0 , H 1 : θ > θ 0 H 1 H_1 H 1 α \alpha α H 0 H_0 H 0 H 0 H_0 H 0 θ = θ 0 \theta=\theta_0 θ = θ 0 g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n ) H 0 H_0 H 0
W = { g ( X 1 , X 2 , ⋯ , X n ) ⩽ g 1 − α } 或 W = { g ( X 1 , X 2 , ⋯ , X n ) ⩾ g α } . W=\left\{g\left(X_1, X_2, \cdots, X_n\right) \leqslant g_{1-\alpha}\right\} \quad \text { 或 } W=\left\{g\left(X_1, X_2, \cdots, X_n\right) \geqslant g_\alpha\right\} \text {. } W = { g ( X 1 , X 2 , ⋯ , X n ) ⩽ g 1 − α } 或 W = { g ( X 1 , X 2 , ⋯ , X n ) ⩾ g α } . 假设检验的四个步骤 经过以上介绍,可以整理出假设检验的下列四个步骤.
第一步:根据给定的问题,建立假设检验问题 ( H 0 , H 1 ) \left(H_0, H_1\right) ( H 0 , H 1 ) ( H 0 , H 1 ) \left(H_0, H_1\right) ( H 0 , H 1 ) H 0 H_0 H 0 g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n ) g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n )
第三步:根据显著性水平 α \alpha α H 0 H_0 H 0 W W W ( x 1 , x 2 , ⋯ , x n ) \left(x_1, x_2, \cdots, x_n\right) ( x 1 , x 2 , ⋯ , x n ) g ( X 1 , X 2 , ⋯ , X n ) g\left(X_1, X_2, \cdots, X_n\right) g ( X 1 , X 2 , ⋯ , X n ) g ( x 1 , x 2 , ⋯ , x n ) g\left(x_1, x_2, \cdots, x_n\right) g ( x 1 , x 2 , ⋯ , x n ) g ( x 1 , x 2 , x n ) ∈ W g\left(x_1, x_2, x_n\right) \in W g ( x 1 , x 2 , x n ) ∈ W H 0 H_0 H 0 H 0 H_0 H 0
例 某食品厂生产的罐头质量(单位: g g g X ∼ N ( μ , 4 ) X \sim N(\mu, 4) X ∼ N ( μ , 4 ) μ = 500 \mu=500 μ = 500 x ˉ = 502 g \bar{x}=502 \mathrm{~g} x ˉ = 502 g α = 0.05 \alpha=0.05 α = 0.05 μ = 500 \mu=500 μ = 500
解: 假设检验问题为 H 0 : μ = 500 , H 1 : μ ≠ 500 H_0: \mu=500, H_1: \mu \neq 500 H 0 : μ = 500 , H 1 : μ = 500 正态抽样 选择统计量以及分布为
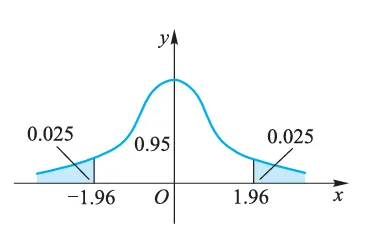
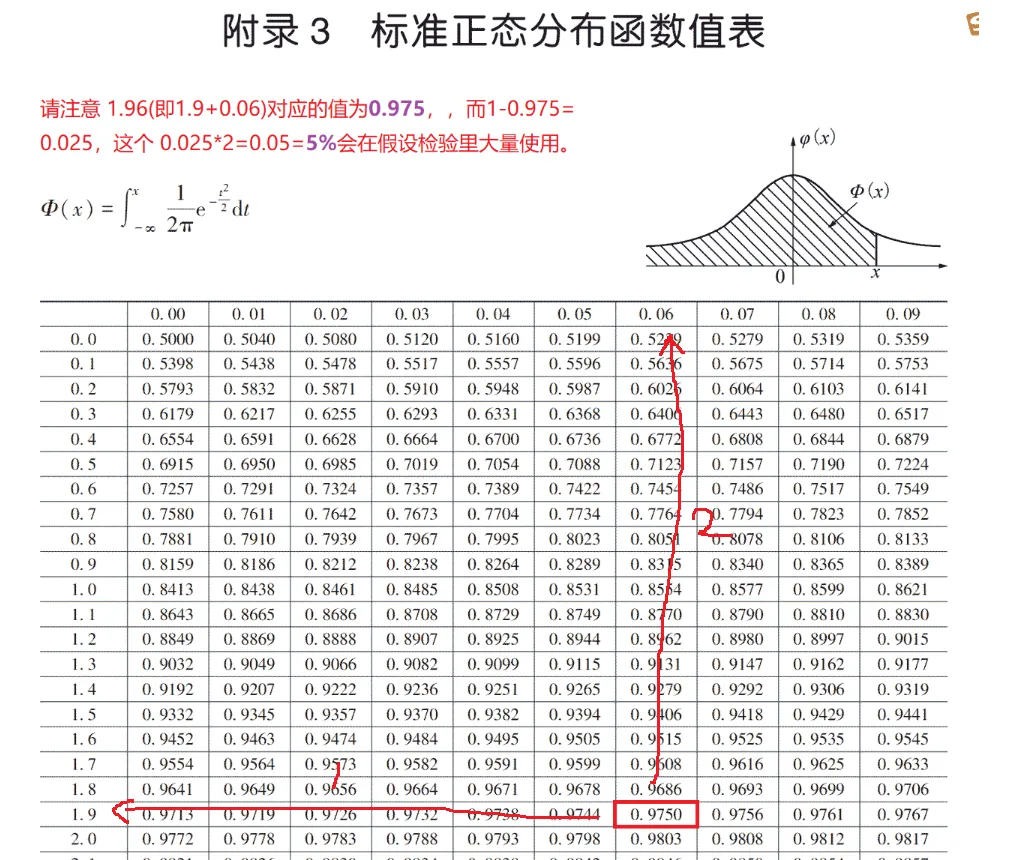
U = X ˉ − μ σ / n = 当 H 0 成立时 X ˉ − 500 σ / n ∼ N ( 0 , 1 ) . U=\frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \xlongequal{\text { 当 } H_0 \text { 成立时 }} \frac{\bar{X}-500}{\sigma / \sqrt{n}} \sim N(0,1) \text {. } U = σ / n X ˉ − μ 当 H 0 成立时 σ / n X ˉ − 500 ∼ N ( 0 , 1 ) . 由于该检验为双侧检验,α = 0.05 \alpha=0.05 α = 0.05 此处 ,下图给出了1.96,在考试时这个数字需要自己查正态表的)
现在切换到正态分布表上,
查表得临界值为 u α 2 = u 0.025 = 1.96 u_{\frac{\alpha}{2}}=u_{0.025}=1.96 u 2 α = u 0.025 = 1.96 u 1 − α 2 = u 0.975 = − u 0.025 = − 1.96 u_{1-\frac{\alpha}{2}}=u_{0.975}=-u_{0.025}=-1.96 u 1 − 2 α = u 0.975 = − u 0.025 = − 1.96
由于该检验为双侧检验,α = 0.05 \alpha=0.05 α = 0.05 u α 2 = u 0.025 = 1.96 u_{\frac{\alpha}{2}}=u_{0.025}=1.96 u 2 α = u 0.025 = 1.96 u 1 − α 2 = u 0.975 = − u 0.025 = − 1.96 u_{1-\frac{\alpha}{2}}=u_{0.975}=-u_{0.025}=-1.96 u 1 − 2 α = u 0.975 = − u 0.025 = − 1.96 H 0 H_0 H 0
W = { U ⩽ − 1.96 或 U ⩾ 1.96 } = { ∣ U ∣ ⩾ 1.96 } . W=\{U \leqslant-1.96 \text { 或 } U \geqslant 1.96\}=\{|U| \geqslant 1.96\} \text {. } W = { U ⩽ − 1.96 或 U ⩾ 1.96 } = { ∣ U ∣ ⩾ 1.96 } . 又 σ = 2. n = 16. x ˉ = 502 \sigma=2 . n=16 . \bar{x}=502 σ = 2. n = 16. x ˉ = 502 u 0 = 502 − 500 2 / 16 = 4 ∈ W u_0=\frac{502-500}{2 / \sqrt{16}}=4 \in W u 0 = 2/ 16 502 − 500 = 4 ∈ W H 0 H_0 H 0 μ = 500 \mu=500 μ = 500
例 某车间用一台包装机包装葡萄糖.包得的袋装质量是一个随机变量,它服从正态分布。当机器正常时,质量 X ∼ N ( 500 , 2 2 ) X \sim N\left(500,2^2\right) X ∼ N ( 500 , 2 2 )
505 , 499 , 502 , 506 , 498 , 498 , 497 , 510 , 503 505,499,502,506,498,498,497,510,503 505 , 499 , 502 , 506 , 498 , 498 , 497 , 510 , 503 假设总体标准差 σ \sigma σ σ = 2 \sigma=2 σ = 2
解:根据上述法则,
由 μ 0 = 500 , σ 0 = 2 , α = 0.05 , n = 9 \mu_0=500, \sigma_0=2, \alpha=0.05, n=9 μ 0 = 500 , σ 0 = 2 , α = 0.05 , n = 9
x ˉ = ( 505 + 499 + 502 + 506 + 498 + 498 + 497 + 510 + 503 ) / 9 = 502. \bar{x}=(505+499+502+506+498+498+497+510+503) / 9=502 . x ˉ = ( 505 + 499 + 502 + 506 + 498 + 498 + 497 + 510 + 503 ) /9 = 502. 检验统计量 U U U
u = 502 − 500 2 / 3 = 3 , ∣ u ∣ = 3 > 1.96 = u 1 − α 2 \begin{gathered}
u=\frac{502-500}{2 / 3}=3, \\
|u|=3>1.96=u_{1-\frac{\alpha}{2}}
\end{gathered} u = 2/3 502 − 500 = 3 , ∣ u ∣ = 3 > 1.96 = u 1 − 2 α 样本点落入拒绝域 W W W H 0 H_0 H 0 H 1 H_1 H 1 α = 0.05 \alpha=0.05 α = 0.05
例 设总体 X X X N ( μ , 1 2 ) , X 1 , X 2 , X 3 , X 4 N\left(\mu, 1^2\right), X_1, X_2, X_3, X_4 N ( μ , 1 2 ) , X 1 , X 2 , X 3 , X 4
H 0 : μ = 0 , H 1 : μ = μ 1 ( μ 1 > 0 ) , H_0: \mu=0, H_1: \mu=\mu_1\left(\mu_1>0\right), H 0 : μ = 0 , H 1 : μ = μ 1 ( μ 1 > 0 ) , 已知拒绝域为 X ˉ > 0.98 \bar{X}>0.98 X ˉ > 0.98 μ 1 = 1 \mu_1=1 μ 1 = 1
解 我们已知,犯第一类错误的概率就是显著性水平 α \alpha α
α = P { 拒绝 H 0 ∣ H 0 为真 } = P { X ˉ > 0.98 ∣ μ = 0 } . \alpha=P\left\{\text { 拒绝 } H_0 \mid H_0 \text { 为真 }\right\}=P\{\bar{X}>0.98 \mid \mu=0\} \text {. } α = P { 拒绝 H 0 ∣ H 0 为真 } = P { X ˉ > 0.98 ∣ μ = 0 } . 由于 μ = 0 \mu=0 μ = 0 X ˉ ∼ N ( 0 , 1 4 ) \bar{X} \sim N\left(0, \frac{1}{4}\right) X ˉ ∼ N ( 0 , 4 1 )
α = P { X ˉ > 0.98 } = 1 − P { X ˉ ⩽ 0.98 } = 1 − Φ ( 0.98 − 0 1 2 ) = 1 − Φ ( 1.96 ) = 0.025. \alpha=P\{\bar{X}>0.98\}=1-P\{\bar{X} \leqslant 0.98\}=1-\Phi\left(\frac{0.98-0}{\frac{1}{2}}\right)=1-\Phi(1.96)=0.025 . α = P { X ˉ > 0.98 } = 1 − P { X ˉ ⩽ 0.98 } = 1 − Φ ( 2 1 0.98 − 0 ) = 1 − Φ ( 1.96 ) = 0.025. 犯第二类错误的概率
β = P { 接受 H 0 ∣ H 0 不真 } = P { 接受 H 0 ∣ H 1 为真 } = P { X ˉ ⩽ 0.98 ∣ μ = μ 1 } , \beta=P\left\{\text { 接受 } H_0 \mid H_0 \text { 不真 }\right\}=P\left\{\text { 接受 } H_0 \mid H_1 \text { 为真 }\right\}=P\left\{\bar{X} \leqslant 0.98 \mid \mu=\mu_1\right\} \text {, } β = P { 接受 H 0 ∣ H 0 不真 } = P { 接受 H 0 ∣ H 1 为真 } = P { X ˉ ⩽ 0.98 ∣ μ = μ 1 } , 由于 μ = μ 1 = 1 \mu=\mu_1=1 μ = μ 1 = 1 X ˉ ∼ N ( 1 , 1 4 ) \bar{X} \sim N\left(1, \frac{1}{4}\right) X ˉ ∼ N ( 1 , 4 1 )
β = P { X ˉ ⩽ 0.98 } = Φ ( 0.98 − 1 1 2 ) = Φ ( − 0.04 ) = 1 − Φ ( 0.04 ) = 0.484 \beta=P\{\bar{X} \leqslant 0.98\}=\Phi\left(\frac{0.98-1}{\frac{1}{2}}\right)=\Phi(-0.04)=1-\Phi(0.04)=0.484 β = P { X ˉ ⩽ 0.98 } = Φ ( 2 1 0.98 − 1 ) = Φ ( − 0.04 ) = 1 − Φ ( 0.04 ) = 0.484