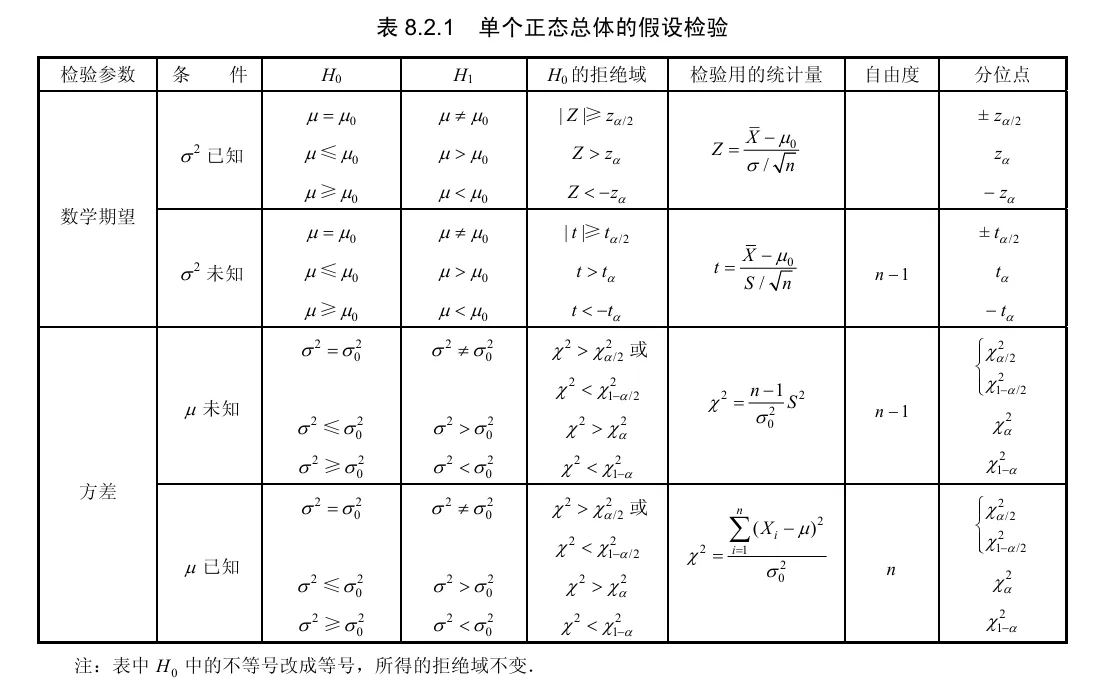
正态检验主要检验μ 和 σ2 他们共有四种情况:
(1) σ2 已知,对 μ 的检验(称做Z检验法或U检验法)
(2) σ2 未知,对 μ 的检验(称做T检验法)
(3) μ 已知,对σ2的检验 (这种情况极少使用)
(4)μ 未知,对σ2的检验(称作χ2 开方检验)
本节介绍方差,上一节介绍均值。
正态检验-方差检验(卡方χ2检验)
双边检验与单边检验
在假设检验中,H0:μ=μ0 ,备择假设 H1:μ=μ0 的意思是 μ 可能大于 μ0 ,也可能小于 μ0 ,称为双边备择假设,并称形如H0:μ=μ0,H1:μ=μ0 的假设检验为双边检验.但有时我们只关心总体均值是否增大,例如,试验新工艺以提高材料的强度,这时所考虑的总体均值应该越大越好,如果我们能判断在新工艺下总体均值较以往正常生产的总体均值大,则可考虑采用新工艺。此时,我们需要检验假设:
H0:μ⩽μ0;H1:μ>μ0....(8.5) 形如(8.5)式的假设检验,称为右边检验。
类似地,有时我们需要检验假设:
H0:μ⩾μ0;H1:μ<μ0...(8.6) 形如(8.6)式的假设检验,称为左边检验.右边检验与左边检验统称为单边检验.
方差检验
设 X∼N(μ,σ2),X1,X2,⋯,Xn 是取自 X 的样本, Xˉ 与 S2 分别为样本均值与样本方差.关于正态方差 σ2 的检验问题,本章讨论如下三种常用形式:
(1)H0:σ2=σ02,H1:σ2=σ02
(2)H0:σ2⩾σ02,H1:σ2<σ02
(3)H0:σ2⩽σ02,H1:σ2>σ02
1. μ未知, H0:σ2=σ02,H1:σ2=σ02
设总体 X∼N(μ,σ2),μ 未知,检验假设:
H0:σ2=σ02;H1:σ2=σ02 其中 σ02 为已知常数.
由于样本方差 S2 是 σ2 的无偏估计量,因此,当 H0 为真时,比值 σ02S2 一般来说应在 1 附近摆动,而不应过分大于 1 或过分小于 1 。因为正态抽样 ,知当 H0 为真时,
χ2=σ02(n−1)S2∼χ2(n−1) 所以对于给定的显著性水平 α ,有(见下图)
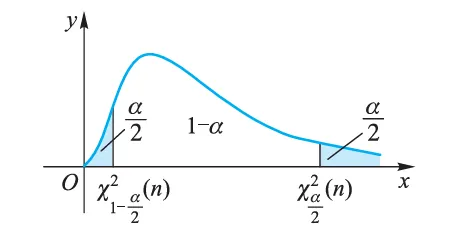
又因对于给定的 α ,查 χ2 分布表(见附表),可求得 χ2 分布的分位点 χ1−2α2(n−1) 与 χ2α2(n−1) ,故 H0 的接受域为
χ1−2α2(n−1)⩽χ2⩽χ2α2(n−1); H0 的拒绝域为
χ2<χ1−2α2(n−1) 或 χ2>χ2α2(n−1). 这种用服从 χ2 分布的统计量对单个正态总体方差进行假设检验的方法,称为 χ2 检验法.
例已知维尼纶的纤度在正常条件下服从正态分布 N(μ,0.0482) 。某日从中随机抽取 5 根,测得其纤度分别为 1.32,1.55,1.36,1.40,1.44 。这一天的维尼纶纤度总体标准差是否正常 (显著性水平 α=0.05 )?
解 待检假设为
H0:σ2=σ02=0.0482;H1:σ2=σ02=0.0482. 由 n=5,α=0.05 ,查表,得 χ0.0252(4)=11.143,χ0.9752(4)=0.484 .
于是,知其拒绝域为
σ02(n−1)S2>11.143 或 σ02(n−1)S2<0.484. 而由样本观察值,得
σ02(n−1)s2≈13.51>11.143. 故拒绝 H0 ,即认为这一天的维尼纶纤度总体标准差不正常.
例某供货商声称他们提供的金属线的质量非常稳定,其抗拉强度的方差为 9 。为了检测抗拉强度,在该金属线中随机地抽出 10 根,测得样本标准差 s=4.5( kg) ,设该金属线的抗拉强度服从正态分布 N(μ,σ2) ,若显著性水平为 α=0.05 ,问:是否可以相信该供货商的说法?
解 由题意知,要检验假设 H0:σ2=9,H1:σ2=9 .
因为 μ 末知,故检验统计量为 χ2=σ02(n−1)S2∼χ2(n−1) .
拒绝域为
χ2>χ2α2(n−1) 或 χ2<χ1−2α2(n−1). 这里 n=10,α=0.05,χ2α2(n−1)=χ0.0252(9)=19.02,χ1−2α2(n−1)=χ0.9752(9)=2.70 .
由样本标准差 s=4.5 ,算得
χ2=99×4.52=20.25. 因为 χ2=20.25>19.02 ,根据 χ2 检验法应拒绝 H0 ,即不相信该供货商的说法.
μ未知,单边检验(右边检验或左边检验)
设总体 X∼N(μ,σ2),μ 未知,检验假设(右边检验):
H0:σ2⩽σ02;H1:σ2>σ02 由于 X∼N(μ,σ2) ,因此,随机变量
χ∗2=σ2(n−1)S2∼χ2(n−1), 故对于给定的显著性水平 α ,有(见图 ).
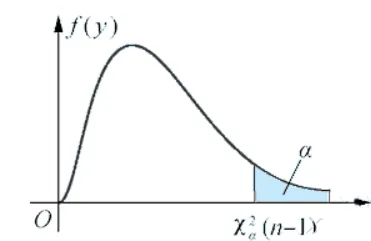
P{χ∗2>χα2(n−1)}=α. 因为当 H0 为真时,统计量
χ2=σ02(n−1)S2⩽χ∗2, 所以有
P{χ2>χα2(n−1)}⩽P{χ∗2>χα2(n−1)}=α. 可见,当 α 很小时,{χ2>χα2(n−1)} 是小概率事件,在一次抽样中认为不可能发生,所以 H0 的拒绝域是
χ2=σ02(n−1)S2>χa2(n−1) (右边检验). 类似地,可得左边检验假设:H0:σ2⩾σ02;H1:σ2<σ02 的拒绝域为
χ2<χ1−α2(n−1) (左边检验). 例 设某种零件的验收标准为长度均值为 10 mm ,标准差小于 0.02 mm .从某厂的一批零件中随机抽出 12 件进行检验,得到如下数据:
9.98,10,9.97,10.05,10.01,9.95,9.99,10.03,10,9.96,10.02,10.03. 已知零件长度服从正态分布.这批零件是否合格(显著性水平 α=0.05 )?
解 由合格需要两个条件:μ=10 及 σ<0.02 ,知 xˉ≈9.9992,s≈0.0306 .
先检验假设:
H0:μ=10;H1:μ=10. 此时方差未知,使用 t 检验法.查自由度为 11 的 t 分布表,得 t0,025(11)=2.201 .计算统计量的观察值,得
t0=0.0306/129.9992−10≈−0.0906 因 ∣t0∣<2.201 ,故不能拒绝原假设 H0:μ=10 ,即零件的平均长度是合格的.
下面再检验假设:
H0:σ<0.02;H1:σ⩾0.02. 查自由度为 11 的 χ2 分布表,得 χ0.052(11)=19.675 .计算统计量的观察值,得
χ02=0.02211×0.03062≈25.75. 因 χ02>χ0,052(11) ,即 χ02 落人拒绝域内,故拒绝原假设,即不能认为这批零件长度的标准差小于 0.02 mm 。因此,这批零件不合格。
例 某供货商声称他们提供的金属线的质量非常稳定,其抗拉强度的方差为 9 .为了检测抗拉强度,在该金属线中随机地抽出 10 根,测得样本标准差 s=4.5( kg) ,设该金属线的抗拉强度服从正态分布 N(μ,σ2) ,若显著性水平为 α=0.05 ,问:是否可以相信该供货商的说法?
解 由题意知,要检验假设 H0:σ2=9,H1:σ2=9 .
因为 μ 末知,故检验统计量为 χ2=σ02(n−1)S2∼χ2(n−1) .
拒绝域为
χ2>χ2α2(n−1) 或 χ2<χ1−2α2(n−1). 这里 n=10,α=0.05,χ2α2(n−1)=χ0.0252(9)=19.02,χ1−2α2(n−1)=χ0.9752(9)=2.70 .
由样本标准差 s=4.5 ,算得
χ2=99×4.52=20.25 因为 χ2=20.25>19.02 ,根据 χ2 检验法应拒绝 H0 ,即不相信该供货商的说法.
例 某厂生产的某种型号的电池,其寿命(以小时计)长期以来服从方差 σ2=5000的正态分布,现有一批这种电池,从它的生产情况来看,寿命的波动性有所改变.现随机取 26 只电池,测出其寿命的样本方差 s2=9200 .问根据这一数据,能否推断这批电池的寿命的波动性较以往的有显著的变化(取 α=0.02 )?
解(1)提出假设 H0:σ=5000,H1:σ2=5000 .
(2)选取统计量
χ2=σ02(n−1)s2 若 H0 为真,则 χ2∼χ2(n−1) .
(3)对给定的显著性水平 α=0.02 ,求 χ1−α/22(n−1)、χα/22(n−1) 使
P{χ2⩽χ1−α/22(n−1)}=2αP{χ2⩾χα/22(n−1)}=2α 这里 χα/22(n−1)=χ0.012(25)=44.314,χ1−α/22(n−1)=χ0.992(25)=11.524 .
(4)计算统计量 χ2 的观察值,代入观察值 s2=9200 ,得
χ2=σ02(n−1)s2=46 (5)判断:由于 46>44.314 ,所以在显著性水平 α=0.02 下拒绝 H0 ,认为这批电池寿命的波动性较以往有显著的变化.
例 某工厂生产金属丝,产品指标为折断力.折断力的方差用来表征工厂生产精度.方差越小,表明精度越高.以往工厂一直把该方差保持在 64( kg2) 或 64 以下.最近从一批产品中抽取 10 根做折断力试验,测得的结果(单位: kg )如下
578,572,570,568,572,570,572,596,584,570. 由上述样本数据算得:
xˉ=575.2,s2=75.74 为此,厂方怀疑金属丝折断力的方差是否变大了.如确实增大了,表明生产精度不如以前,就需对生产流程做一番检验,以发现生产环节中存在的问题(显著性水平 α=0.05 ).
解 为确认上述疑虑是否为真,假定多金属丝折断力服从正态分布,并做下述假设检验: H0:σ2⩽64, H1:σ2>64.
上述假设检验问题可利用 χ2 检验法的右侧检验法来检验,就本例而言,相应于 σ02=64 , n=10 .
对于给定的显著性水平 α=0.05 ,查附录知
χα2(n−1)=χ0.052(9)=16.919. 从而有 χ2=σ02n−1s2=649×75.74=10.65⩽16.919=χ0.052 ,故不能拒绝原假设 H0 ,从而认为样本方差的偏大是偶然因素,生产流程正常,故不需再做进一步检查.
例一位生物学家研究生活在高原上的某一甲虫, 从高原上采集了 n=20 个高山甲虫,以考察高山上的该甲虫是否不同于平原上的该甲虫,其中度量方法之一是翅膀上黑斑的长度. 已知平原甲虫黑斑长度服从期望 μ0=3.14mm ,方差 σ02=0.0505mm2 的正态分布,从高山上甲虫样本得到的黑斑长度 xˉ=3.23mm,s=0.4mm ,假定高山甲虫黑斑长度服从正态分布 N(μ,σ2), 在显著性水平 α=0.05 下分别进行下列检验:
(1) H0:μ=3.14↔H1:μ=3.14;
(2) H0:σ2=0.0505mm2↔H1:σ2=0.0505mm2.
解 (1) 取检验统计量 T=Sn(Xˉ−3.14), 拒绝域为
W={∣T∣>t1−α/2(n−1)}. 今 t1−α/2(n−1)=t0.975(19)=2.093. 计算 t 检验统计量的观测值为
t=0.420(3.23−3.14)=0.98<2.093. 因而不能拒绝 H0, 认为在显著水平 α=0.05 下, 高山甲虫的黑斑长度的均值是 3.14 mm .
(2)取检验统计量 χ2=0.0505(n−1)S2 ,拒绝域为
W={χ2>χ1−α/22(n−1) 或 χ2<χα/22(n−1)}, 查附录 可得 χ0.9752(19)=32.852,χ0.0252(19)=8.907 ,计算 χ2 检验统计量的观测值为
χ2=0.050519⋅0.42=60.1980>32.852. 因而拒绝 H0 ,认为在显著性水平 α=0.05 下,高山甲虫的黑斑长度的方差不再是 0.0505mm2 。
μ 已知,方差的检验
以上讨论的是在均值未知的情况下对方差的假设检验,这种情况在实际问题中较多.至于均值已知的情况下,对方差的假设检验,其方法类似,只是所选的统计量为
χ2=σ02∑i=1n(Xi−μ)2. 当 σ2=σ02 为真时,χ2∼χ2(n) .
关于单个正态总体的假设检验如附表。
附表
具体见附表