在实际应用当中,我们还常常会遇到两个正态总体的参数比较问题,例如,比较两个品牌的同排量汽车的平均耗油量的优劣;又如,比较两台仪器测量精度的高低,等等.这些问题都可以在单个正态总体参数检验的基础上加以推广。
两个都是正态分布,通常有3种检验类型
(1)σ 1 2 , σ 2 2 \sigma_1^2, \sigma_2^2 σ 1 2 , σ 2 2 μ 1 − μ 2 \mu_1-\mu_2 μ 1 − μ 2 σ 1 2 , σ 2 2 \sigma_1^2, \sigma_2^2 σ 1 2 , σ 2 2 σ 1 2 = σ 2 2 \sigma_1^2=\sigma_2^2 σ 1 2 = σ 2 2 μ 1 − μ 2 \mu_1-\mu_2 μ 1 − μ 2 μ 1 , μ 2 \mu_1, \mu_2 μ 1 , μ 2 σ 1 2 σ 2 2 \frac{\sigma_1^2}{\sigma_2^2} σ 2 2 σ 1 2
上一节 介绍了(1)(2)检验法,本节 介绍(3) 检验法
两个正态总体方差的假设检验 设 X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) , X 1 , X 2 , ⋯ , X n 1 X \sim N\left(\mu_1, \sigma_1^2\right), Y \sim N\left(\mu_2, \sigma_2^2\right), X_1, X_2, \cdots, X_{n_1} X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) , X 1 , X 2 , ⋯ , X n 1 X X X Y 1 , Y 2 , ⋯ , Y n 2 Y_1, Y_2, \cdots, Y_{n_2} Y 1 , Y 2 , ⋯ , Y n 2 Y Y Y X ˉ \bar{X} X ˉ Y ˉ \bar{Y} Y ˉ X 1 , X 2 , ⋯ , X n 1 X_1, X_2, \cdots, X_{n_1} X 1 , X 2 , ⋯ , X n 1 Y 1 , Y 2 , ⋯ , Y n 2 Y_1, Y_2, \cdots, Y_{n_2} Y 1 , Y 2 , ⋯ , Y n 2 S 1 2 S_1^2 S 1 2 S 2 2 S_2^2 S 2 2
关于正态方差 σ 1 \sigma_1 σ 1 σ 2 \sigma_2 σ 2 H 0 : σ 1 2 = σ 2 2 , H 1 : σ 1 2 ≠ σ 2 2 H_0: \sigma_1^2=\sigma_2^2, H_1: \sigma_1^2 \neq \sigma_2^2 H 0 : σ 1 2 = σ 2 2 , H 1 : σ 1 2 = σ 2 2 H 0 : σ 1 2 ⩽ σ 2 2 , H 1 : σ 1 2 > σ 2 2 H_0: \sigma_1^2 \leqslant \sigma_2^2, H_1: \sigma_1^2>\sigma_2^2 H 0 : σ 1 2 ⩽ σ 2 2 , H 1 : σ 1 2 > σ 2 2 H 0 : σ 1 2 ⩾ σ 2 2 , H 1 : σ 1 2 < σ 2 2 H_0: \sigma_1^2 \geqslant \sigma_2^2, H_1: \sigma_1^2<\sigma_2^2 H 0 : σ 1 2 ⩾ σ 2 2 , H 1 : σ 1 2 < σ 2 2 H 0 : σ 1 2 σ 2 2 = 1 , H 1 : σ 1 2 σ 2 2 ≠ 1 H_0: \frac{\sigma_1^2}{\sigma_2^2}=1, H_1: \frac{\sigma_1^2}{\sigma_2^2} \neq 1 H 0 : σ 2 2 σ 1 2 = 1 , H 1 : σ 2 2 σ 1 2 = 1 H 0 : σ 1 2 σ 2 2 ⩽ 1 , H 1 : σ 1 2 σ 2 2 > 1 H_0: \frac{\sigma_1^2}{\sigma_2^2} \leqslant 1, H_1: \frac{\sigma_1^2}{\sigma_2^2}>1 H 0 : σ 2 2 σ 1 2 ⩽ 1 , H 1 : σ 2 2 σ 1 2 > 1 H 0 : σ 1 2 σ 2 2 ⩾ 1 , H 1 : σ 1 2 σ 2 2 < 1 H_0: \frac{\sigma_1^2}{\sigma_2^2} \geqslant 1, H_1: \frac{\sigma_1^2}{\sigma_2^2}<1 H 0 : σ 2 2 σ 1 2 ⩾ 1 , H 1 : σ 2 2 σ 1 2 < 1
H 0 : σ 1 2 = σ 2 2 ; H 1 : σ 1 2 ≠ σ 2 2 H_0: \sigma_1^2=\sigma_2^2 ; \quad H_1: \sigma_1^2 \neq \sigma_2^2 H 0 : σ 1 2 = σ 2 2 ; H 1 : σ 1 2 = σ 2 2 由 S 1 2 S_1^2 S 1 2 S 2 2 S_2^2 S 2 2 σ 1 2 \sigma_1^2 σ 1 2 σ 2 2 \sigma_2^2 σ 2 2 H 0 H_0 H 0
F = S 1 2 / S 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) F=S_1^2 / S_2^2 \sim F\left(n_1-1, n_2-1\right) F = S 1 2 / S 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) 故选取 F F F F F F F F F H 0 H_0 H 0 F F F H 1 H_1 H 1 F F F
F ⩽ k 1 或 F ⩾ k 2 ( k 1 , k 2 待定) F \leqslant k_1 \text { 或 } F \geqslant k_2 \quad\left(k_1, k_2\right. \text { 待定) } F ⩽ k 1 或 F ⩾ k 2 ( k 1 , k 2 待定 ) 对于给定的显著性水平 α \alpha α
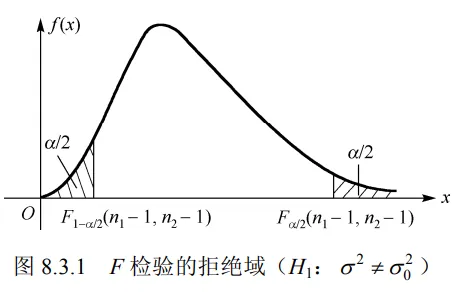
P { F ⩽ F 1 − α / 2 ( n 1 − 1 , n 2 − 1 ) 或 F ⩾ F α / 2 ( n 1 − 1 , n 2 − 1 ) } = α , P\left\{F \leqslant F_{1-\alpha / 2}\left(n_1-1, n_2-1\right) \text { 或 } F \geqslant F_{\alpha / 2}\left(n_1-1, n_2-1\right)\right\}=\alpha \text {, } P { F ⩽ F 1 − α /2 ( n 1 − 1 , n 2 − 1 ) 或 F ⩾ F α /2 ( n 1 − 1 , n 2 − 1 ) } = α , 如图 8.3.1 所示,拒绝域为
W = { F ⩽ F 1 − α / 2 ( n 1 − 1 , n 2 − 1 ) 或 F ⩾ F α / 2 ( n 1 − 1 , n 2 − 1 ) } . . . . ( 8.3.1 ) W=\left\{F \leqslant F_{1-\alpha / 2}\left(n_1-1, n_2-1\right) \text { 或 } F \geqslant F_{\alpha / 2}\left(n_1-1, n_2-1\right)\right\} . ...(8.3.1) W = { F ⩽ F 1 − α /2 ( n 1 − 1 , n 2 − 1 ) 或 F ⩾ F α /2 ( n 1 − 1 , n 2 − 1 ) } .... ( 8.3.1 ) 根据一次抽样后得到的样本观察值 x 1 , x 2 , ⋯ , x n 1 x_1, x_2, \cdots, x_{n_1} x 1 , x 2 , ⋯ , x n 1 y 1 , y 2 , ⋯ , y n 2 y_1, y_2, \cdots, y_{n_2} y 1 , y 2 , ⋯ , y n 2 F F F H 0 H_0 H 0 H 0 H_0 H 0
H 0 : σ 1 2 ⩽ σ 2 2 , H 1 : σ 1 2 > σ 2 2 H_0: \sigma_1^2 \leqslant \sigma_2^2, \quad H_1: \sigma_1^2>\sigma_2^2 H 0 : σ 1 2 ⩽ σ 2 2 , H 1 : σ 1 2 > σ 2 2 对应的拒绝域为
W = { F ⩾ F α ( n 1 − 1 , n 2 − 1 ) } . W=\left\{F \geqslant F_\alpha\left(n_1-1, n_2-1\right)\right\} . W = { F ⩾ F α ( n 1 − 1 , n 2 − 1 ) } . (3)检验假设
H 0 : σ 1 2 ⩾ σ 2 2 , H 1 : σ 1 2 < σ 2 2 H_0: \sigma_1^2 \geqslant \sigma_2^2, \quad H_1: \sigma_1^2<\sigma_2^2 H 0 : σ 1 2 ⩾ σ 2 2 , H 1 : σ 1 2 < σ 2 2 对应的拒绝域为
W = { F ⩽ F 1 − α ( n 1 − 1 , n 2 − 1 ) } . W=\left\{F \leqslant F_{1-\alpha}\left(n_1-1, n_2-1\right)\right\} . W = { F ⩽ F 1 − α ( n 1 − 1 , n 2 − 1 ) } . 例两台机床加工同种零件,分别从两台车床加工的零件中抽取 6 个和 9 个测量其直径,并计算得 s 1 2 = 0.345 , s 2 2 = 0.375 s_1^2=0.345, s_2^2=0.375 s 1 2 = 0.345 , s 2 2 = 0.375 α = 0.10 \alpha=0.10 α = 0.10
解 设两总体 X X X Y Y Y N ( μ 1 , σ 1 2 ) N\left(\mu_1, \sigma_1^2\right) N ( μ 1 , σ 1 2 ) N ( μ 2 , σ 2 2 ) , μ 1 , μ 2 , σ 1 2 , σ 2 2 N\left(\mu_2, \sigma_2^2\right), \mu_1, ~ \mu_2, ~ \sigma_1^2, ~ \sigma_2^2 N ( μ 2 , σ 2 2 ) , μ 1 , μ 2 , σ 1 2 , σ 2 2 H 0 : σ 1 2 = σ 2 2 , H 1 : σ 1 2 ≠ σ 2 2 H_0: \sigma_1^2=\sigma_2^2, ~ H_1: \sigma_1^2 \neq \sigma_2^2 H 0 : σ 1 2 = σ 2 2 , H 1 : σ 1 2 = σ 2 2 F = S 1 1 / S 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) F=S_1^1 / S_2^2 \sim F\left(n_1-1, n_2-1\right) F = S 1 1 / S 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) α \alpha α k 1 , k 2 k_1, ~ k_2 k 1 , k 2 P { F < k 1 P\left\{F<k_1\right. P { F < k 1 F > k 2 } = α \left.F>k_2\right\}=\alpha F > k 2 } = α
k 1 = F 1 − α / 2 ( n 1 − 1 , n 2 − 1 ) = F 0.95 ( 5 , 8 ) = 1 F 0.05 ( 8 , 5 ) = 0.208 , k 2 = F α / 2 ( n 1 − 1 , n 2 − 1 ) = F 0.05 ( 5 , 8 ) = 3.69 , \begin{gathered}
k_1=F_{1-\alpha / 2}\left(n_1-1, n_2-1\right)=F_{0.95}(5,8)=\frac{1}{F_{0.05}(8,5)}=0.208, \\
k_2=F_{\alpha / 2}\left(n_1-1, n_2-1\right)=F_{0.05}(5,8)=3.69,
\end{gathered} k 1 = F 1 − α /2 ( n 1 − 1 , n 2 − 1 ) = F 0.95 ( 5 , 8 ) = F 0.05 ( 8 , 5 ) 1 = 0.208 , k 2 = F α /2 ( n 1 − 1 , n 2 − 1 ) = F 0.05 ( 5 , 8 ) = 3.69 , 从而拒绝域为 F < 0.208 F<0.208 F < 0.208 F > 3.69 F>3.69 F > 3.69 s 1 2 = 0.345 , s 2 2 = 0.375 s_1^2=0.345, s_2^2=0.375 s 1 2 = 0.345 , s 2 2 = 0.375 F = s 1 2 / s 2 2 = 0.92 F=s_1^2 / s_2^2=0.92 F = s 1 2 / s 2 2 = 0.92 0.208 < 0.92 < 3.69 0.208<0.92<3.69 0.208 < 0.92 < 3.69 H 0 H_0 H 0
例新,旧两个水稻品种进行对比试验,旧品种其分成 25 个小区,样本均值为 x ˉ 1 = 36.65 k g \bar{x}_1=36.65 kg x ˉ 1 = 36.65 k g s 1 = 2.32 k g s_1=2.32 kg s 1 = 2.32 k g x ˉ 2 = 37.65 k g \bar{x}_2=37.65 kg x ˉ 2 = 37.65 k g s 2 = 1.89 k g s_2=1.89 kg s 2 = 1.89 k g α = 0.05 \alpha=0.05 α = 0.05
解 待检假设为
H 0 : σ 1 2 = σ 2 2 ; H 1 : σ 1 2 ≠ σ 2 2 H_0: \sigma_1^2=\sigma_2^2 ; H_1: \sigma_1^2 \neq \sigma_2^2 H 0 : σ 1 2 = σ 2 2 ; H 1 : σ 1 2 = σ 2 2 这里 n 1 = 25 , n 2 = 20 , s 1 = 2.32 , s 2 = 1.89 n_1=25, n_2=20, s_1=2.32, s_2=1.89 n 1 = 25 , n 2 = 20 , s 1 = 2.32 , s 2 = 1.89 F = S 1 2 S 2 2 F=\frac{S_1^2}{S_2^2} F = S 2 2 S 1 2 f 0 = 2.32 2 1.89 2 ≈ 1.507 f_0=\frac{2.32^2}{1.89^2} \approx 1.507 f 0 = 1.8 9 2 2.3 2 2 ≈ 1.507 α = 0.05 \alpha=0.05 α = 0.05 F ˉ \bar{F} F ˉ
F α 2 ( n 1 − 1 , n 2 − 1 ) = F 0.025 ( 24 , 19 ) = 2.45 F 1 − α 2 ( n 1 − 1 , n 2 − 1 ) = F 0.975 ( 24 , 19 ) = 0.41 \begin{aligned}
& F_{\frac{\alpha}{2}}\left(n_1-1, n_2-1\right)=F_{0.025}(24,19)=2.45 \\
& F_{1-\frac{\alpha}{2}}\left(n_1-1, n_2-1\right)=F_{0.975}(24,19)=0.41
\end{aligned} F 2 α ( n 1 − 1 , n 2 − 1 ) = F 0.025 ( 24 , 19 ) = 2.45 F 1 − 2 α ( n 1 − 1 , n 2 − 1 ) = F 0.975 ( 24 , 19 ) = 0.41 由于 f 0 ≈ 1.507 ∈ ( 0.41 , 2.45 ) f_0 \approx 1.507 \in(0.41,2.45) f 0 ≈ 1.507 ∈ ( 0.41 , 2.45 ) H 0 H_0 H 0 σ 1 2 = σ 2 2 \sigma_1^2=\sigma_2^2 σ 1 2 = σ 2 2
例 在某种制造过程中需要比较两种钢板的强度:一种是冷轧钢板;另一种是双面镀锌钢板.现从冷轧钢板中抽取 20 个样品,测得强度的均值为 x ˉ = 20.5 ( G P a ) \bar{x}=20.5(\mathrm{GPa}) x ˉ = 20.5 ( GPa ) y ˉ = 23.9 ( G P a ) \bar{y}=23.9(\mathrm{GPa}) y ˉ = 23.9 ( GPa ) σ 1 2 = 2.8 2 , σ 2 2 = 3.5 2 \sigma_1{ }^2=2.8^2, \sigma_2{ }^2=3.5^2 σ 1 2 = 2. 8 2 , σ 2 2 = 3. 5 2 ( α = 0.01 ) (\alpha=0.01) ( α = 0.01 )
解 由题意知,要检验的假设为 H 0 : μ 1 = μ 2 , H 1 : μ 1 ≠ μ 2 H_0: \mu_1=\mu_2, H_1: \mu_1 \neq \mu_2 H 0 : μ 1 = μ 2 , H 1 : μ 1 = μ 2 σ 1 2 , σ 2 2 \sigma_1^2, \sigma_2^2 σ 1 2 , σ 2 2 H 0 H_0 H 0
U = X ˉ − Y ˉ σ 1 2 n 1 + σ 2 2 n 2 ∼ N ( 0 , 1 ) . U=\frac{\bar{X}-\bar{Y}}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \sim N(0,1) . U = n 1 σ 1 2 + n 2 σ 2 2 X ˉ − Y ˉ ∼ N ( 0 , 1 ) . 因为 α = 0.01 , u α 2 = u 0.005 = 2.58 \alpha=0.01, u_{\frac{\alpha}{2}}=u_{0.005}=2.58 α = 0.01 , u 2 α = u 0.005 = 2.58 ∣ U ∣ > u α 2 |U|>u_{\frac{\alpha}{2}} ∣ U ∣ > u 2 α ∣ U ∣ > 2.58 |U|>2.58 ∣ U ∣ > 2.58
u = 20.5 − 23.9 2.8 2 20 + 3.5 2 25 = − 3.62 u=\frac{20.5-23.9}{\sqrt{\frac{2.8^2}{20}+\frac{3.5^2}{25}}}=-3.62 u = 20 2. 8 2 + 25 3. 5 2 20.5 − 23.9 = − 3.62 由于 ∣ u ∣ > 2.58 |u|>2.58 ∣ u ∣ > 2.58 H 0 H_0 H 0
例 有两种灯泡,一种用 A 型灯丝,另一种用 B 型灯丝。随机抽取两种灯泡各 10 个做试验,测得它们的寿命(单位:h h h
A 型: 1293 , 1380 , 1614 , 1497 , 1340 , 1643 , 1466 , 1677 , 1387 , 1711 1293,1380,1614,1497,1340,1643,1466,1677,1387,1711 1293 , 1380 , 1614 , 1497 , 1340 , 1643 , 1466 , 1677 , 1387 , 1711 1061 , 1065 , 1092 , 1017 , 1021 , 1138 , 1143 , 1094 , 1028 , 1119 1061,1065,1092,1017,1021,1138,1143,1094,1028,1119 1061 , 1065 , 1092 , 1017 , 1021 , 1138 , 1143 , 1094 , 1028 , 1119 ( α = 0.05 ) \quad(\alpha=0.05) ( α = 0.05 )
解 由题意知,要检验的假设为 H 0 : μ 1 = μ 2 , H 1 : μ 1 ≠ μ 2 H_0: \mu_1=\mu_2, H_1: \mu_1 \neq \mu_2 H 0 : μ 1 = μ 2 , H 1 : μ 1 = μ 2 σ 1 2 , σ 2 2 \sigma_1^2, \sigma_2^2 σ 1 2 , σ 2 2 σ 1 2 = σ 2 2 \sigma_1^2=\sigma_2^2 σ 1 2 = σ 2 2 H 0 H_0 H 0
T = X ˉ − Y ˉ S w 1 n 1 + 1 n 2 ∼ t ( n 1 + n 2 − 2 ) T=\frac{\bar{X}-\bar{Y}}{S_w \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \sim t\left(n_1+n_2-2\right) T = S w n 1 1 + n 2 1 X ˉ − Y ˉ ∼ t ( n 1 + n 2 − 2 ) 且
S w 2 = ( n 1 − 1 ) S 1 2 + ( n 2 − 1 ) S 2 2 n 1 + n 2 − 2 S_w^2=\frac{\left(n_1-1\right) S_1^2+\left(n_2-1\right) S_2^2}{n_1+n_2-2} S w 2 = n 1 + n 2 − 2 ( n 1 − 1 ) S 1 2 + ( n 2 − 1 ) S 2 2 拒绝域为
∣ T ∣ > t α 2 ( n 1 + n 2 − 2 ) |T|>t_{\frac{\alpha}{2}}\left(n_1+n_2-2\right) ∣ T ∣ > t 2 α ( n 1 + n 2 − 2 ) 这里 n 1 = n 2 = 10 , α = 0.05 , t α 2 ( n 1 + n 2 − 2 ) = t 0.025 ( 18 ) = 2.101 n_1=n_2=10, \alpha=0.05, t_{\frac{\alpha}{2}}\left(n_1+n_2-2\right)=t_{0.025}(18)=2.101 n 1 = n 2 = 10 , α = 0.05 , t 2 α ( n 1 + n 2 − 2 ) = t 0.025 ( 18 ) = 2.101 x ˉ = 1500.8 , y ˉ = 1077.8 \bar{x}=1500.8, \bar{y}=1077.8 x ˉ = 1500.8 , y ˉ = 1077.8 s 1 2 = 151.3 2 , s 2 2 = 47.0 2 s_1^2=151.3^2, s_2^2=47.0^2 s 1 2 = 151. 3 2 , s 2 2 = 47. 0 2
∣ t ∣ = 1500.8 − 1077.8 151.3 2 × 9 + 47.0 2 × 9 18 1 10 + 1 10 ≈ 8.45 > 2.101 = t 0.025 ( 18 ) |t|=\frac{1500.8-1077.8}{\sqrt{\frac{151.3^2 \times 9+47.0^2 \times 9}{18}} \sqrt{\frac{1}{10}+\frac{1}{10}}} \approx 8.45>2.101=t_{0.025}(18) ∣ t ∣ = 18 151. 3 2 × 9 + 47. 0 2 × 9 10 1 + 10 1 1500.8 − 1077.8 ≈ 8.45 > 2.101 = t 0.025 ( 18 ) 故拒绝 H 0 H_0 H 0
例某一橡胶制品配方中,原配方用氧化锌 5 g ,现配方减为 1 g .现分别对两种配方做一批试验,分别测得橡胶制品的伸长率如下。
现配方: 565 , 577 , 580 , 575 , 556 , 542 , 560 , 532 , 470 , 461 565,577,580,575,556,542,560,532,470,461 565 , 577 , 580 , 575 , 556 , 542 , 560 , 532 , 470 , 461 540 , 533 , 525 , 520 , 545 , 531 , 541 , 529 , 534 540,533,525,520,545,531,541,529,534 540 , 533 , 525 , 520 , 545 , 531 , 541 , 529 , 534 ( α = 0.1 ) \quad(\alpha=0.1) ( α = 0.1 ) H 0 : σ 1 2 = σ 2 2 , H 1 : σ 1 2 ≠ σ 2 2 H_0: \sigma_1^2=\sigma_2^2, H_1: \sigma_1^2 \neq \sigma_2^2 H 0 : σ 1 2 = σ 2 2 , H 1 : σ 1 2 = σ 2 2 μ 1 , μ 2 \mu_1, \mu_2 μ 1 , μ 2 H 0 H_0 H 0
F = S 1 2 S 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) F=\frac{S_1^2}{S_2^2} \sim F\left(n_1-1, n_2-1\right) F = S 2 2 S 1 2 ∼ F ( n 1 − 1 , n 2 − 1 ) 拒绝域为
F < F 1 − α 2 ( n 1 − 1 , n 2 − 1 ) 或 F > F α 2 ( n 1 − 1 , n 2 − 1 ) . F<F_{1-\frac{\alpha}{2}}\left(n_1-1, n_2-1\right) \text { 或 } F>F_{\frac{\alpha}{2}}\left(n_1-1, n_2-1\right) \text {. } F < F 1 − 2 α ( n 1 − 1 , n 2 − 1 ) 或 F > F 2 α ( n 1 − 1 , n 2 − 1 ) . 这里 n 1 = 10 , n 2 = 9 , α = 0.1 n_1=10, n_2=9, \alpha=0.1 n 1 = 10 , n 2 = 9 , α = 0.1
F α 2 ( n 1 − 1 , n 2 − 1 ) = F 0.05 ( 9 , 8 ) = 3.39 , F 1 − α 2 ( n 1 − 1 , n 2 − 1 ) = F 0.95 ( 9 , 8 ) = 1 F 0.05 ( 8 , 9 ) = 1 3.23 . F_{\frac{\alpha}{2}}\left(n_1-1, n_2-1\right)=F_{0.05}(9,8)=3.39, \quad F_{1-\frac{\alpha}{2}}\left(n_1-1, n_2-1\right)=F_{0.95}(9,8)=\frac{1}{F_{0.05}(8,9)}=\frac{1}{3.23} . F 2 α ( n 1 − 1 , n 2 − 1 ) = F 0.05 ( 9 , 8 ) = 3.39 , F 1 − 2 α ( n 1 − 1 , n 2 − 1 ) = F 0.95 ( 9 , 8 ) = F 0.05 ( 8 , 9 ) 1 = 3.23 1 . 由样本值可算得 s 1 2 = 236.8 , s 2 2 = 63.86 s_1^2=236.8, s_2^2=63.86 s 1 2 = 236.8 , s 2 2 = 63.86
f = s 1 2 s 2 2 = 236.8 63.86 ≈ 3.7 > 3.39 f=\frac{s_1^2}{s_2^2}=\frac{236.8}{63.86} \approx 3.7>3.39 f = s 2 2 s 1 2 = 63.86 236.8 ≈ 3.7 > 3.39 故拒绝 H 0 H_0 H 0
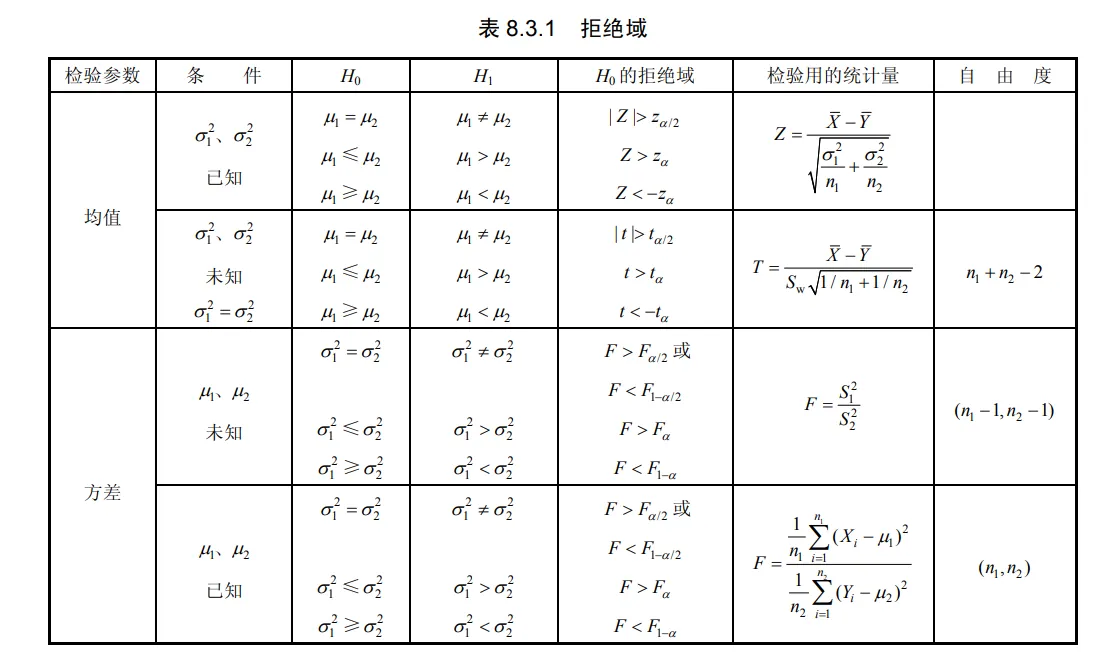
注意:当 μ 1 \mu_1 μ 1 μ 2 \mu_2 μ 2 H 0 : σ 1 2 = σ 2 2 H_0: \sigma_1^2=\sigma_2^2 H 0 : σ 1 2 = σ 2 2
F = 1 n 1 ∑ i = 1 n 1 ( X i − μ 1 ) 2 1 n 2 ∑ i = 1 n 2 ( Y i − μ 2 ) 2 ∼ F ( n 1 , n 2 ) , F=\frac{\frac{1}{n_1} \sum_{i=1}^{n_1}\left(X_i-\mu_1\right)^2}{\frac{1}{n_2} \sum_{i=1}^{n_2}\left(Y_i-\mu_2\right)^2} \sim F\left(n_1, n_2\right), F = n 2 1 ∑ i = 1 n 2 ( Y i − μ 2 ) 2 n 1 1 ∑ i = 1 n 1 ( X i − μ 1 ) 2 ∼ F ( n 1 , n 2 ) , 其拒绝域如表 8.3.1 所示.