3.8_推广与应用

3.8 推广与应用*

3.8.1 最小二乘问题的推广

正则化

在求解超定线性方程组时, 我们极小化 ∥Ax−b∥22\| Ax - b\| _2^2 而对于欠定线性方程组, 由于解不唯一, 我们往往还需要极小化 ∥x∥22\| x\| _2^2 两者合起来就是

min⁡x∈Rn12∥Ax−b∥22+α2∥x∥22,(3.31)\min _ {x \in \mathbb {R} ^ {n}} \frac {1}{2} \| A x - b \| _ {2} ^ {2} + \frac {\alpha}{2} \| x \| _ {2} ^ {2}, \tag {3.31}

其中 α>0\alpha > 0 是正则化参数. 对应的目标函数记为

J(x)=∥Ax−b∥22+α∥x∥22.J (x) = \| A x - b \| _ {2} ^ {2} + \alpha \| x \| _ {2} ^ {2}.

当 α>0\alpha > 0 时, J(x)J(x) 是一个严格凸的二次函数, 因此存在唯一的最小值点. 令 J(x)J(x) 关于 xx 的一阶导数为零, 则可得

(ATA+αI)x=ATb.(A ^ {\mathsf {T}} A + \alpha I) x = A ^ {\mathsf {T}} b.

由于 ATA+αIA^{\mathsf{T}}A + \alpha I 对称正定, 故非奇异. 所以问题 (3.30) 的唯一解为

x=(ATA+αI)−1ATb.x = (A ^ {\mathsf {T}} A + \alpha I) ^ {- 1} A ^ {\mathsf {T}} b.

加权正则化

一类应用更广泛的问题是下面的加权正则化问题

min⁡x∈Rn12∥Ax−b∥22+α2∥Wx∥22,(3.32)\min _ {x \in \mathbb {R} ^ {n}} \frac {1}{2} \| A x - b \| _ {2} ^ {2} + \frac {\alpha}{2} \| W x \| _ {2} ^ {2}, \tag {3.32}

其中 α>0\alpha > 0 是正则化参数, W∈Rm×nW \in \mathbb{R}^{m \times n} 是广义加权矩阵, 可以是非负对角矩阵, 对称正定矩阵,也可以是一般矩阵 (如一阶差分算子, 二阶差分算子等). 需要指出的是, WW 不一定要求是方阵.经过类似的推导, 可知问题 (3.31) 的解满足

(ATA+αWTW)x=ATb.\left(A ^ {\mathsf {T}} A + \alpha W ^ {\mathsf {T}} W\right) x = A ^ {\mathsf {T}} b.

如果 ATA+αWTWA^{\mathsf{T}}A + \alpha W^{\mathsf{T}}W 非奇异, 则存在唯一解

x=(ATA+αWTW)−1ATb.x = \left(A ^ {\mathsf {T}} A + \alpha W ^ {\mathsf {T}} W\right) ^ {- 1} A ^ {\mathsf {T}} b.

约束最小二乘问题

考虑带有约束的最小二乘问题

min⁡x∈Rn12∥Ax−b∥22(3.33)\min _ {x \in \mathbb {R} ^ {n}} \frac {1}{2} \| A x - b \| _ {2} ^ {2} \tag {3.33}
s . t .Bx=f\begin{array}{l l} \text {s . t .} & B x = f \end{array}

其中 Bx=fBx = f 是约束条件, B∈Rp×nB \in \mathbb{R}^{p \times n} 和 f∈Rpf \in \mathbb{R}^p 都是给定的. 对应的 Lagrange 函数为

J(x)=12∥Ax−b∥22+λT(Bx−f).J (x) = \frac {1}{2} \| A x - b \| _ {2} ^ {2} + \lambda^ {\mathsf {T}} (B x - f).

分别对 xx 和 λ\lambda 求一阶导数，并令其等于零，可得

[ATABTB0][xλ]=[ATbf].\left[ \begin{array}{c c} A ^ {\mathsf {T}} A & B ^ {\mathsf {T}} \\ B & 0 \end{array} \right] \left[ \begin{array}{c} x \\ \lambda \end{array} \right] = \left[ \begin{array}{c} A ^ {\mathsf {T}} b \\ f \end{array} \right].

如果 ATAA^{\mathsf{T}}A 非奇异, 且 BB 行满秩, 则存在唯一解

λ=[B(ATA)−1BT]−1[B(ATA)−1ATb−f]\lambda = \left[ B (A ^ {\mathsf {T}} A) ^ {- 1} B ^ {\mathsf {T}} \right] ^ {- 1} \left[ B (A ^ {\mathsf {T}} A) ^ {- 1} A ^ {\mathsf {T}} b - f \right]
x=(ATA)−1(ATb−BTλ).x = (A ^ {\mathsf {T}} A) ^ {- 1} (A ^ {\mathsf {T}} b - B ^ {\mathsf {T}} \lambda).

3.8.2 最小二乘问题的应用

多项式数据拟合

最小二乘的一个重要应用就是低次多项式数据拟合: 已知平面上 nn 个点 {(ti,fi)}i=1n\{(t_i, f_i)\}_{i=1}^n , 寻找一个低次多项式来拟合这些数据.

设拟合多项式为

p(x)=a0+a1t+a2t2+⋯+amtm.p (x) = a _ {0} + a _ {1} t + a _ {2} t ^ {2} + \dots + a _ {m} t ^ {m}.

通常 m≪nm \ll n . 将上述 nn 个点 {(ti,fi)}i=1n\{(t_i, f_i)\}_{i=1}^n 代入可得

[1t1t12…t1m1t2t22…t2m⋮⋮⋮⋮1tntn2…tnm]n×(m+1)[a0a1⋮am]=[f1f2⋮fn]\left[ \begin{array}{c c c c c} 1 & t _ {1} & t _ {1} ^ {2} & \dots & t _ {1} ^ {m} \\ 1 & t _ {2} & t _ {2} ^ {2} & \dots & t _ {2} ^ {m} \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & t _ {n} & t _ {n} ^ {2} & \dots & t _ {n} ^ {m} \end{array} \right] _ {n \times (m + 1)} \left[ \begin{array}{c} a _ {0} \\ a _ {1} \\ \vdots \\ a _ {m} \end{array} \right] = \left[ \begin{array}{c} f _ {1} \\ f _ {2} \\ \vdots \\ f _ {n} \end{array} \right]

或 Ax=fAx = f

其中 A∈Rn×(m+1)A \in \mathbb{R}^{n \times (m + 1)} , x=[a0,a1,…,am]⊤x = [a_0, a_1, \ldots, a_m]^\top . 由于 m≪nm \ll n , 该方程组是超定的, 解通常是不存在的. 因此, 我们寻找一个近似解, 使得残量 ∥f−Ax∥2\|f - Ax\|_2 最小, 即求解最小二乘问题

min⁡x∈Rm+1∥f−Ax∥22\min_{x\in \mathbb{R}^{m + 1}}\| f - Ax\|_{2}^{2}

线性预测

预测一个时间序列的未来走向, 其中一个常用方法就是线性预测 (linear prediction). 假定一个时间序列在 tkt_k 时刻的值 fkf_k 线性依赖于其前 mm 个时刻的值 fk−1,fk−2,…,fk−mf_{k-1}, f_{k-2}, \ldots, f_{k-m} , 即

fk=a1fk−1+a2fk−2+⋯+amfk−m.(3.34)f _ {k} = a _ {1} f _ {k - 1} + a _ {2} f _ {k - 2} + \dots + a _ {m} f _ {k - m}. \tag {3.34}

现在已经测得该时间序列的前 nn 个值 fi,i=0,1,2,…,n−1f_{i}, i = 0,1,2,\ldots,n-1 , 如何预测其未来的取值. 这里 n≫mn \gg m . 将现有的数据代入关系式 (3.33) 可得

[fm−1fm−2fm−3…f0fmfm−1fm−2…f1⋮⋮⋮⋮fn−2fn−3fn−4…fn−m−1](n−m)×m[a1a2⋮am]=[fmfm+1⋮fn−1]或Ax=f,\left[ \begin{array}{c c c c c} {f _ {m - 1}} & {f _ {m - 2}} & {f _ {m - 3}} & {\dots} & {f _ {0}} \\ {f _ {m}} & {f _ {m - 1}} & {f _ {m - 2}} & {\dots} & {f _ {1}} \\ {\vdots} & {\vdots} & {\vdots} & & {\vdots} \\ {f _ {n - 2}} & {f _ {n - 3}} & {f _ {n - 4}} & {\dots} & {f _ {n - m - 1}} \end{array} \right] _ {(n - m) \times m} \left[ \begin{array}{l} {a _ {1}} \\ {a _ {2}} \\ {\vdots} \\ {a _ {m}} \end{array} \right] = \left[ \begin{array}{l} {f _ {m}} \\ {f _ {m + 1}} \\ {\vdots} \\ {f _ {n - 1}} \end{array} \right] \quad \text {或} \quad A x = f,

其中 A∈R(n−m)×m,x=[a1,a2,…,am]⊤A \in \mathbb{R}^{(n - m) \times m}, x = [a_1, a_2, \ldots, a_m]^\top . 这也是一个超定问题, 其解也是通过求解下面的最小二乘问题来获取

min⁡x∈Rm∥f−Ax∥22\min _ {x \in \mathbb {R} ^ {m}} \| f - A x \| _ {2} ^ {2}

信号恢复

在获取数字信号时, 由于各种各样的原因, 最后得到的信号总会带有一定的噪声, 即

b=x+η,b = x + \eta ,

其中 xx 是真实的信号, bb 是观察到的信号, η\eta 是噪声.

去噪是数字信号和图像处理中的一个基本问题, 其中一个有效方法就是加权最小二乘法, 即

min⁡x12∥x−b∥22+12α∥Dx∥22,\min _ {x} \frac {1}{2} \| x - b \| _ {2} ^ {2} + \frac {1}{2} \alpha \| D x \| _ {2} ^ {2},

其中 DD 是离散的二阶导算子或TV算子

例3.8 数字信号去噪

(LS_denoise.m)

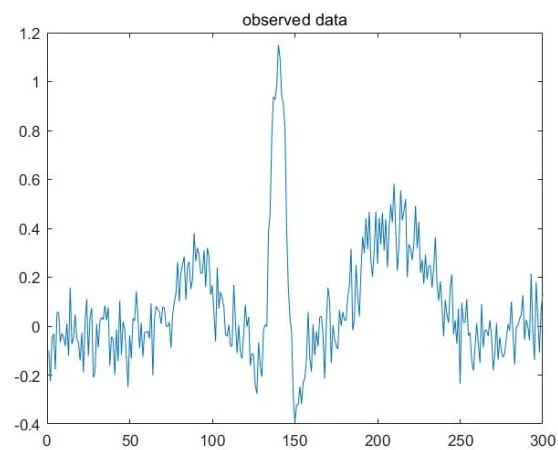
图像恢复

除了带噪声以外, 在获取数字图像时也经常会由于各种原因 (设备仪器, 拍摄环境等) 导致图像模糊. 通常数字图像的获取模型为

f=B(x)+η,f = \mathcal {B} (x) + \eta ,

其中 xx 是真实图像, ff 是观察到的图像, B(⋅)\mathcal{B}(\cdot) 是卷积算子 (代表模糊机制), η\eta 是噪声.

由于问题本身是不适定的, 因此求解时需要进行正则化, 常用的模型有 Tikhonov 正则化模型:

min⁡∥B(x)−f∥22+μ2∥x∥22\min \left\| \mathcal {B} (x) - f \right\| _ {2} ^ {2} + \mu^ {2} \| x \| _ {2} ^ {2}

或加权正则化模型：

min⁡∥B(x)−f∥22+μ2∥Dx∥22,\min \| \mathcal {B} (x) - f \| _ {2} ^ {2} + \mu^ {2} \| D x \| _ {2} ^ {2},

其中 DD 是广义加权矩阵，可以是非负对角矩阵或TV算子等

例3.9 数字图像去噪和去模糊


(a)


(b)


(a)


(a) 真实图像
(b)


(b) 模糊机制 (out-of-focus)
(c)

(a) 获取到的图像 (带有噪声和模糊)
(b) 恢复后的图像 (基于 Tikhonov 正则化模型)
(c) 恢复后的图像 (基于加权正则化模型)

前の章3.7_最小二乘扰动分析
次の章3.9_课后习题