4.2_CUDA并行编程
4.2 CUDA并行编程
前面我们看到将一个标准C函数放到GPU设备上运行是很容易的。只需在函数定义前面加上__global__修饰符,并通过一种特殊的尖括号语法来调用它,就可以在GPU上执行这个函数。这种方法虽然非常简单,但同样也是很低效的,因为NVIDIA的硬件工程师们早已对图形处理器进行优化,使其可以同时并行执行数百次的计算。然而,我们在这个示例中只调用了一个核函数,并且该函数在GPU上以串行方式运行。在本章中,我们将看到如何启动一个并行执行的设备核函数。
4.2.1 矢量求和运算
我们通过一个简单示例来说明线程的概念,以及如何使用CUDA来实现线程。假设有两组数据,我们需要将这两组数据中对应的元素两两相加,并将结果保存在第三个数组中。在图4.1中给出了这个计算过程。如果你学过线性代数,就会发现这实际上是一个矢量求和运算。

图4.1 两个矢量的求和
1. 基于CPU的矢量求和
首先,我们来看看如何通过传统的C代码来实现这个求和运算:
include"../common/book.h" #define N10 void add(int \*a,int \*b,int \*c){int tid $= 0$ : //这是第0个CPU.因此索引从0开始
while(tid $\leqslant$ N){c[tid] $\equiv$ a[tid] $^+$ b[tid];tid $+ = 1$ : //由于只有一个CPU,因此每次递增1}
}
int main(void){inta[N],b[N],c[N];//在CPU上为数组‘a’和‘b’赋值for(inti=0;i<N;i++){a[i] $\equiv$ -i;b[i] $\equiv$ i\*i;
}add(a,b,c);//显示结果for(inti=0;i<N;i++) {printf("%d+%d=%d\n",a[i],b[i],c[i]);
}return 0;这段示例代码几乎不需要任何解释,但我们将对函数add()做简要分析,看看为什么这个函数有些过于复杂。
void add(int \*a,int \*b,int \*c){int tid $= 0$ //这是第0个CPU,因此索引从0开始while(tid<N){c[tid] $=$ a[tid] $^+$ b[tid];tid $+ = 1$ //由于只有一个CPU,因此每次递增1}函数在一个while循环中计算总和,其中索引tid的取值范围为0到N-1。我们将a[]和b[]的对应元素相加起来,并将结果保存在c[]的相应元素中。通常,可以用更简单的方式来编写这段代码,例如:
void add(int \*a,int \*b,int \*c){ for $(\mathrm{i} = 0$ : $\mathrm{i} < \mathrm{N}$ ; $\mathrm{i + + })$ { $\mathbf{c}[\mathbf{i}] = \mathbf{a}[\mathbf{i}] + \mathbf{b}[\mathbf{i}];$ 1
1上面采用的while循环虽然有些复杂,但这是为了使代码能够在拥有多个CPU或者CPU核的系统上并行运行。例如,在双核处理器上可以将每次递增的大小改为2,这样其中一个核从tid=0开始执行循环,而另一个核从tid=1开始执行循环。第一个核将偶数索引的元素相加,而第二个核则将奇数索引的元素相加。这相当于在每个CPU核上执行以下代码:
第1个CPU核 第2个CPU核
void add(int \*a,int \*b,int \*c) void add(int \*a,int \*b,int \*c){ int tid $= 0$ · int tid $= 1$ · while (tid $< N$ ){ while(tid $< N$ ){ c[tid] $= a[$ tid] $^+$ b[tid]; tid $+ = 2$ · tid $+ = 2$ · }
}当然,要在CPU上实际执行这个运算,还需要增加更多的代码。例如,需要编写一定数量的代码来创建工作线程,每个线程都执行函数add(),并假设每个线程都将并行执行。然而,这种假设是一种理想但不实际的想法,线程调度机制的实际运行情况往往并非如此。
2. 基于GPU的矢量求和
我们可以在GPU上实现相同的加法运算,这需要将add()编写为一个设备函数。这段代码与前一章中的代码非常类似。在给出设备代码之前,我们首先给出函数main()。虽然main()在GPU上的实现与在CPU上的实现是不同的,但在下面的代码中并没有包含新内容:
include"../common/book.h"
#define N 10
int main(void){ int a[N],b[N],c[N]; int \*dev_a,\*dev_b,\*dev_c; //在GPU上分配内存 HANDLE_ERROR( CUDAAlloc( (void\*\*)&dev_a,N\*sizeof(int))); HANDLE_ERROR( CUDAAlloc( (void\*\*)&dev_b,N\*sizeof(int))); HANDLE_ERROR( CUDAAlloc( (void\*\*)&dev_c,N\*sizeof(int))); //在CPU上为数组‘a’和‘b’赋值 for(int $i = 0$ ;i<N;i++){ a[i]=-i; b[i]=i\*i;
} //将数组‘a’和‘b’复制到GPUHANDLE_ERROR(udaMemcpy(dev_a,a,N\*sizeof(int),udaMemcpyHostToDevice));
HANDLE_ERROR(udaMemcpy(dev_b,b,N\*sizeof(int),udaMemcpyHostToDevice));
add<<N,1>>>(dev_a,dev_b,dev_c);
//将数组‘c’从GPU复制到CPU
HANDLE_ERROR(udaMemcpy(c,dev_c,N\*sizeof(int),udaMemcpyDeviceToHost));
//显示结果
for(int $\mathrm{i} = 0$ :i<N;i++){printf("%d+%d=%d\n",a[i],b[i],c[i]);
}
//释放在GPU上分配的内存
udaFree(dev_a);
udaFree(dev_b);
udaFree(dev_c);
return 0;需要注意的是,上面的代码中再次使用了一些通用模式:
调用CUDAAlloc()在设备上为三个数组分配内存:在其中两个数组(dev_a和dev_b)中包含了输入值,而在数组dev_c中包含了计算结果。
为了避免内存泄露,在使用完GPU内存后通过CUDAFree()释放它们。
通过CUDAMemcpy()将输入数据复制到设备中,同时指定参数CUDAMemcpyHostToDevice,在计算完成后,将计算结果通过参数CUDAMemcpyDeviceToHost复制回主机。
通过尖括号语法,在主机代码main()中执行add()中的设备代码。
你可能会奇怪为什么要在CPU上对输入数组赋值。其实,这么做并没有什么特殊原因。事实上,如果在GPU上为数组赋值,这个步骤执行得会更快些。但这段代码的目的是说明如何在图形处理器上实现两个矢量的加法运算。因此,我们假设这个加法运算只是其他应用程序中的一个步骤,并且输入数组a[]和b[]可以由其他算法生成,或者由用户从硬盘上读取。我们假设这些数据已经存在了,现在需要对它们执行某种操作。
接下来是add()函数,这个函数看上去非常类似于基于CPU实现的add()。
__global__void add(int \*a,int \*b,int \*c){ int tid $=$ blockIdx.x; //计算该索引处的数据 if(tid $< \mathbb{N}$ ) $c[\mathrm{tid}] = a[\mathrm{tid}] + b[\mathrm{tid}]$ ·我们再次看到在函数add()中使用了一种通用模式:
编写的一个在设备上执行的函数add()。我们采用C来编写代码,并在函数名字前添加了一个修饰符 global。
到目前为止,除了执行的计算不是将2和7相加外,在这个示例中没有包含任何新的东西。然而,这个示例中有两个值得注意的地方:尖括号中的参数以及核函数中包含的代码,这两处地方都引入了新的概念。
我们曾看到过通过以下形式启动的核函数:
kernel<<1,1>>>(param1,param2,...);但在这个示例中,尖括号中的数值并不是1:
add<<N,1>>>(dev_a,dev_b,dev_c);这两个数值代表什么含义?
我们在前面并没有对尖括号中的这两个数值进行解释,而只是很含糊地指出,这两个参数将传递给运行时,作用是告诉运行时如何启动核函数。事实上,在这两个参数中,第一个参数表示设备在执行核函数时使用的并行线程块的数量。在这个示例中,指定这个参数为N。
例如,如果指定的是kernel<<2,1>>(),那么可以认为运行时将创建核函数的两个副本,并以并行方式来运行它们。我们将每个并行执行环境都称为一个线程块(Block)。如果指定的是kernel<<256,1>>(),那么将有256个线程块在GPU上运行。然而,并行计算从来都不是一个简单的问题。
这种运行方式引出了一个问题:既然GPU将运行核函数的N个副本,那如何在代码中知道当前正在运行的是哪一个线程块?这个问题的答案在于示例中核函数的代码本身。具体来说,是在于变量blockIdx.x:
__global__ void add(int *a, int *b, int *c) {
int tid = blockIdx.x; //计算位于这个索引处的数据
if (tid < N)
c[ tid] = a[ tid] + b[ tid];
}乍一看,在编译这个函数时似乎会出现错误,因为代码将变量的值赋给了tid,但之前却没
有定义它。然而,这里不需要定义变量blockIdx,它是一个内置变量,在CUDA运行时中已经预先定义了这个变量。而且,这个变量名字的含义也就是变量的作用。变量中包含的值就是当前执行设备代码的线程块的索引。
你可能会问,为什么不是blockIdx?而是blockIdx.x?事实上,这是因为CUDA支持二维的线程块数组。对于二维空间的计算问题,例如矩阵数学运算或者图像处理,使用二维索引往往会带来很大的便利,因为它可以避免将线性索引转换为矩形索引。即使你不熟悉这些问题类型也不必担心,你只需知道在某些情况下,使用二维索引比使用一位索引要更为方便。当然,你并不是必须使用它。
当启动核函数时,我们将并行线程块的数量指定为N。这个并行线程块集合也称为一个线程格(Grid)。这是告诉运行时,我们想要一个一维的线程格,其中包含N个线程块。每个线程块的blockIdx.x值都是不同的,第一个线程块的blockIdx.x为0,而最后一个线程块的blockIdx.x为N-1。因此,假设有4个线程块,并且所有线程块都运行相同的设备代码,但每个线程块的blockIdx.x的值是不同的。当四个线程块并行执行时,运行时将用相应的线程块索引来替换blcokIdx.x,每个线程块实际执行的代码如下所示。
第1个线程块 第2个线程块
__global__ void __global__ void
add(int *a, int *b, int *c) {
int tid = 0;
if (tid < N)
c[tid] = a[tid] + b[tid];
}
如果回顾前面给出的基于CPU的示例,你会发现在基于CPU的示例中需要遍历从0到N-1的索引从而对两个矢量求和。而在基于GPU的示例中,运行时已经启动了一个核函数,其中每个线程块都拥有0到N-1中的一个索引,因此这几乎将所有的遍历工作都已经完成了。这显然是一件好事,使得我们有更多的时间去写博客,而写的内容或许正是关于如何节约编码的时间。
最后一个需要回答的问题是,为什么要判断tid是否小于N?在通常情况下,tid总是小于N的,因为在核函数中都是这么假设的。然而,我们仍然怀疑是否有人会破坏代码中作出的假设。
破坏假设意味着破坏代码,意味着在代码中出现错误,而我们也不得不工作到深夜去找出代码中的问题,因此也没有时间登录博客。如果没有检查tid是否小于N,并且最终发生了内存非法访问,那么将造成一种糟糕的情况。事实上,这种情况可能会终止核函数的运行,因为GPU有着完善的内存管理机制,它将强行结束所有违反内存访问规则的进程。
如果出现了这类问题,那么代码中的HANDLE_ERROR()宏将检测出这种情况并发出警告信息。与传统的C编程一样,这里的函数会由于某种原因而返回错误码。虽然你通常会忽视这些错误码,但我们还是建议检查每个失败操作的结果,这样就不会像我们曾经一样经历数小时的痛苦时间。由于这种情况经常发生,而这些错误的出现通常也无法阻止应用程序的继续执行,但在大多数情况下,它们将对程序的后续执行造成各种不可预期的糟糕后果。
此时,你或许正在GPU上并行运行代码。你可能听说过在GPU上运行代码是很复杂的,或者有人告诉你必须理解计算机图形学才能在图形处理器上实现通用算法编程。我们希望你开始意识到,CUDA C的出现使得在GPU上编写并行代码变得更加容易。我们在这里给出的示例只是对长度为10的矢量进行相加。如果想编写更大规模的并行应用程序,那么也是非常容易的,只需将#define N 10中的10改为10000或者50000,这样可以启动数万个并行线程块。然而,需要注意的是:在启动线程块数组时,数组每一维的最大数量都不能超过65535。这是一种硬件限制,如果启动的线程块数量超过了这个限值,那么程序将运行失败。在下一章中,我们将看到如何在这种限制范围内工作。
# 4.2.2 一个有趣的示例
我们并不认为将矢量相加是一个无趣的示例,但下面这个示例将满足那些希望看到并行CUDA更有趣应用的读者。
在接下来的示例中将介绍如何绘制Julia集的曲线。对于不熟悉Julia集的读者,可以简单地将Julia集认为是满足某个复数计算函数的所有点构成的边界。显然,这听起来似乎比矢量相加和矩阵乘法更为无趣。然而,对于函数参数的所有取值,生成的边界将形成一种不规则的碎片形状,这是数学中最有趣和最漂亮的形状之一。
生成Julia集的算法非常简单。Julia集的基本算法是,通过一个简单的迭代等式对复平面中的点求值。如果在计算某个点时,迭代等式的计算结果是发散的,那么这个点就不属于Julia集合。也就是说,如果在迭代等式中计算得到的一系列值朝着无穷大的方向增长,那么这个点就被认为不属于Julia集合。相反,如果在迭代等式中计算得到的一系列值都位于某个边界范围之内,那么这个点就属于Julia集合。
从计算上来看,这个迭代等式非常简单,如等式4.1所示:
等式4.1
$$
Z _ {n + 1} = Z _ {n} ^ {2} + C
$$
可以看到,计算等式4.1的迭代过程包括,首先计算当前值的平方,然后再加上一个常数以得到等式的下一个值。
# 1.基于CPU的Julia集
我们将分析一段计算Julia集的源代码。由于这个程序比到目前为止看到的其他程序都更为复杂,因此我们将其分解为多个代码段。在本章的后面部分将给出完整的源代码。
```cpp
int main(void) { CPUBitmap bitmap(DIM, DIM); unsigned char \*ptr $=$ bitmap.get_ptr(); kernel( ptr ); bitmap.display_and_exit();
}main函数非常简单。它通过工具库创建了一个大小合适的位图图像。接下来,它将一个指向位图数据的指针传递给了核函数。
void kernel(unsigned char *ptr) {
for (int y=0; y<DIM; y++) {
for (int x=0; x<DIM; x++) {
int offset = x + y * DIM;
int juliaValue = julia(x, y);
ptr[offset*4 + 0] = 255 * juliaValue;
ptr[offset*4 + 1] = 0;
ptr[offset*4 + 2] = 0;
ptr[offset*4 + 3] = 255;
}
}
}核函数对将要绘制的所有点进行迭代,并在每次迭代时调用julia()来判断该点是否属于Julia集。如果该点位于集合中,那么函数julia()将返回1,否则将返回0。如果julia()返回1,那么将点的颜色设置为红色,如果返回0则设置为黑色。这些颜色是任意的,你可以根据自己的喜好来选择合适的颜色。
int julia(int x, int y) {const float scale $= 1.5$
float $\mathrm{jx} =$ scale \* (float) $(\mathrm{DIM / 2 - x}) / (\mathrm{DIM / 2})$ . float $\mathrm{jy} =$ scale \* (float) $(\mathrm{DIM / 2 - y}) / (\mathrm{DIM / 2})$ cuComplex c(-0.8, 0.156);
cuComplex a(jx, jy);
int i $= 0$
for $(\mathrm{i} = 0$ ; $\mathrm{i < 200}$ ; $\mathrm{i + + }$ { a $=$ a \* a $^+$ c; if (amagnitude2()>1000) return 0;
}
return 1;
}这个函数是示例程序的核心。函数首先将像素坐标转换为复数空间的坐标。为了将复平面的原点定位到图像中心,我们将像素位置移动了 。然后,为了确保图像的范围为-1.0到1.0,我们将图像的坐标缩放了 倍。这样,给定一个图像点 ,就可以计算并得到复空间中的一个点 。
然后,我们引入了一个scale因数来实现图形的缩放。当前,这个scale被硬编码为1.5,当然你也可以调整这个参数来缩小或者放大图形。更完善的做法是将其作为一个命令行参数。
在计算出复空间中的点之后,需要判断这个点是否属于Julia集。在前面提到过,这是通过计算迭代等式 来判断的。C是一个任意的复数常量,我们选择的值是 因为这个值刚好能生成一张有趣的图片。如果想看看其他的Julia集,那么可以修改这个常量。
在这个示例中,我们计算了200次迭代。在每次迭代计算完成后,都会判断结果是否超过某个阀值(在这里是1000)。如果超过了这个阀值,那么等式就是发散的,因此将返回0以表示这个点不属于Julia集合。反之,如果所有的200次迭代都计算完毕后,并且结果仍然小于1000,那么我们就认为这个点属于该集合,并且给调用者kernel()返回1。
由于所有计算都是在复数上进行的,因此我们定义了一个通用结构来保存复数值。
struct cuComplex {
float r;
float i;
cuComplex(float a, float b) : r(a), i(b) {}
float magnitude2(void) { return r * r + i * i; }
cuComplex operator*(const cuComplex& a) {return cuComplex(r*a.r - i*a.i, i*a.r + r*a.i); } cuComplex operator+ (const cuComplex& a) { return cuComplex(r*a.r, i+a.i); } }这个类表示一个复数值,包含两个成员:单精度的实部r和单精度的虚部i。在这个类中定义了复数的加法运算符和乘法运算符。(如果你完全不熟悉复数值,那么可以在网上快速学习一本入门书)。最后,我们还定义了一个方法来返回复数的模。
2. 基于GPU的Julia集
在GPU设备上计算Julia集的代码与CPU版本的代码非常类似。
int main(void) { CPUBitmap bitmap(DIM, DIM); unsigned char \*devitemap;
HANDLE_ERROR(udaMalloc(void\*\*)&devitemap, bitmap(image_size())); dim3 grid(DIM, DIM); kernel<<grid,1>>>(devitemap);
HANDLE_ERROR(udaMemcpy bitmap.get_ptr(), devitemap, bitmap,image_size(),udaMemcpyDeviceToHost)); bitmap.display_and_exit();
CUDAFree( devitemap);
}这个版本的main()看上去比基于CPU的版本要更复杂,但实际上程序的执行流程是相同的。与CPU版本一样,首先通过工具库创建一个DIM x DIM大小的位图图像。然而,由于接下来将在GPU上执行计算,因此在代码中声明了一个指针dev bitmap,用来保存设备上数据的副本。同样,为了保存数据,我们需要通过CUDAAlloc()来分配内存。
然后,我们像在CPU版本中那样来运行Kernel()函数,但是它现在是一个__global__函数,这意味着将在GPU上运行。与CPU示例一样,在前面代码中分配的指针会传递给kernel()来保存计算结果。唯一的差异在于这线程块内存驻留在GPU上,而不是在主机上。
这里最需要注意的是,在程序中指定了多个并行线程块来执行函数kernel()。由于每个点的计算与其他点的计算都是相互独立的,因此可以为每个需要计算的点都执行该函数的一个副本。之前提到过,在某些情况中使用二维索引会带来一定的帮助。显然,在二维空间(例如复平面)中计算函数值正属于这种情况。因此,在下面这行代码中声明了一个二维的线程格:
dim3 grid(DIM, DIM);类型dim3并不是标准C定义的类型。在CUDA头文件中定义了一些辅助类型来封装多维数组。类型dim3表示一个三维数组,可以用于指定启动的线程块的数量。然而,为什么要使用三维数组,而我们实际需要的只是一个二维线程格?
坦白地说,这么做是因为CUDA运行时希望得到一个三维的dim3值。虽然当前并不支持三维的线程格,但CUDA运行时仍然希望得到一个dim3类型的参数,只不过最后一维的大小为1。当仅用两个值来初始化dim3类型的变量时,例如在语句dim3 grid(DIM, DIM)中,CUDA运行时将自动把第3维的大小指定为1。虽然NVIDIA在将来或许会支持3维的线程格,但就目前而言,我们只能暂且满足这个API的要求,因为每当开发人员和API做斗争时,胜利的一方总是API。
然后,在下面这行代码中将dim3变量grid传递给CUDA运行时:
kernel<<grid,1>>>(dev bitmap);最后,在执行完kernel()之后,在设备上会生成计算结果,我们需要将这些结果复制回主机。和前面一样,通过cudaMemcpy()来实现这个操作,并将复制方向指定为cudaMemcpyDeviceToHost。
HANDLE_ERROR(udaMemcpy( bitmap.get_ptr(), dev bitmap, bitmap(image_size(),udaMemcpyDeviceToHost));在基于CPU的版本与基于GPU的版本之间,关键差异之一在于kernel()的实现。
__global__void kernel(unsigned char *ptr) //将threadIdx/BlockIdx映射到像素位置 int $\mathbf{x} =$ blockIdx.x; int $\mathrm{y} =$ blockIdx.y; int offset $= x + y$ \* gridDim.x; //现在计算这个位置上的值 int juliaValue $=$ julia(x,y); ptr[offset\*4+0] $= 255$ \* juliaValue; ptr[offset\*4+1] $= 0$ ptr[offset\*4+2] $= 0$ ptr[offset\*4+3] $= 255$首先,我们要将Kernel()声明为一个__global__函数,从而可以从主机上调用并在设备上运行。与CPU版本不同的是,我们不需要通过嵌套的for()循环来生成像素索引以传递给julia()。与矢量相加示例一样,CUDA运行时将在变量blockIdx中包含这些索引。这种方式是可行的,因为在声明线程格时,线程格每一维的大小与图像每一维的大小是相等的,因此在(0,0)和(DIM-1,DIM-1)之间的每个像素点(x,y)都能获得一个线程块。
接下来,唯一需要的信息就是要得到输出缓冲区ptr中的线性偏移。这个偏移值是通过另一个内置变量gridDim来计算的。对所有的线程块来说,gridDim是一个常数,用来保存线程格每一维的大小。在来示例中,gridDim的值是(DIM,DIM)。因此,将行索引乘以线程格的宽度,再加上列索引,就得到了ptr中的唯一索引,其取值范围为(DIM*DIM-1)。
int offset = x + y * gridDim.x;最后,我们来分析判断某个点是否属于Julia集的代码。这段代码看上去与CPU版本是相同的。
device int julia(int x, int y) { const float scale = 1.5; float jx = scale * (float)(DIM/2 - x)/(DIM/2); float jy = scale * (float)(DIM/2 - y)/(DIM/2); cuComplex c(-0.8, 0.156); cuComplex a(jx, jy); int i = 0; for (i=0; i<200; i++) { a = a * a + c; if (amagnitude2() > 1000) return 0; } return 1;我们定义了一个cuComplex结构,在结构中同样使用单精度浮点数来保存复数的实部和虚部。这个结构也定义了加法运算符和乘法运算符,此外还定义了一个函数来返回复数值的模。
struct cuComplex {
float r;
float i;
cuComplex(float a, float b): r(a), i(b) {}
__device__ float magnitude2(void) {}return r \*r+i\*i;
} _device cuComplex operator\*(const cuComplex& a){ return cuComplex(r\*a.r - i\*a.i, i\*a.r + r\*a.i); } _device cuComplex operator+(const cuComplex& a){ return cuComplex(r+a.r, i+a.i);
};注意,我们使用了在CPU版本中已经用过的相同的语言结构。二者差异之一在于修饰符__device__,这表示代码将在GPU而不是主机上运行。由于这些函数已声明为__device__函数,因此只能从其他__device__函数或者从__global__函数中调用它们。
综上所述,以下给出了完整的源代码清单:
include"../common/book.h"
#include"../common/cpuBITmap.h"
#define DIM 1000
struct cuComplex{ float r; float i; cuComplex(float a,float b):r(a),i(b){ _devicefloat magnitude2(void){ return $\textbf{r} *\textbf{r} +\textbf{i} *\textbf{i};$ } _device cuComplex operator\* (const cuComplex& a) { return cuComplex(r*a.r-i*a.i,i*a.r+r*a.i); } _device cuComplex operator+(const cuComplex& a) { return cuComplex(r+a.r,i+a.i); };
_ device int julia(int x,int y){ const float scale $= 1.5$ float jx $=$ scale \* (float)(DIM/2-x)/(DIM/2); float jy $=$ scale \* (float)(DIM/2-y)/(DIM/2); cuComplex c(-0.8,0.156); cuComplex a(jx,jy);int i = 0;
for (i=0; i<200; i++) {
a = a * a + c;
if (amagnitude2() > 1000)
return 0;
}
return 1;
}
__global__ void kernel(unsigned char *ptr) {
// 将threadIdx/BlockIdx映射到像素位置
int x = blockIdx.x;
int y = blockIdx.y;
int offset = x + y * gridDim.x;
// 现在计算这个位置上的值
int juliaValue = julia(x, y);
ptr[offset*4 + 0] = 255 * juliaValue;
ptr[offset*4 + 1] = 0;
ptr[offset*4 + 2] = 0;
ptr[offset*4 + 3] = 255;
}
int main(void) {
CPUBitmap bitmap(DIM, DIM);
unsigned char *dev_bitmap;
HANDLE_ERROR(cudaMalloc((void**)&dev_bitmap, bitmap(image_size())));
dim3 grid(DIM, DIM);
kernel<<grid, l>>>(dev_bitmap);
HANDLE_ERROR(cudaMemcpy bitmap.get_ptr(), dev_bitmap, bitmap(image_size(),udaMemcpyDeviceToHost));
bitmap.display_and_exit();
HANDLE_ERROR(cudaFree(dev_bitmap));
}当运行这个应用程序时,你将看到Julia集的动画演示。为了使你相信它确实称得上是“一个有趣的示例”,图4.2给出了这个应用程序的运行截屏。
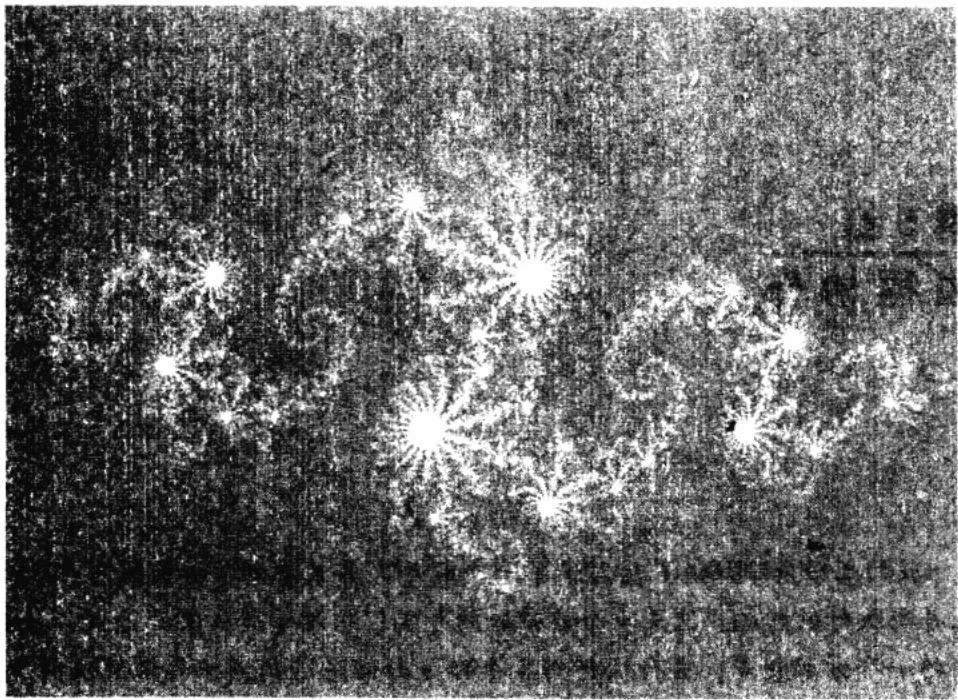
图4.2 基于GPU的Julia集应用程序的截屏