6.4 反向传播的实现

这样就做好准备工作了。下面我们尝试通过反向传播对图6-1的计算求导。

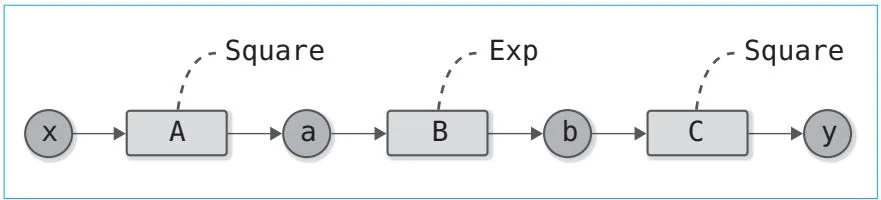
图6-1 进行反向传播的复合函数

首先编写图6-1所示的正向传播的代码

steps/step06.py

A = Square()

B  $=$  Exp()

C = Square()

$\mathbf{x} =$  Variable(np.array(0.5))

a = A(x)

b = B(a)

$y = C(b)$

接着通过反向传播计算y的导数。为此，我们需要按照与正向传播相反的顺序调用各函数的backward方法。图6-2是这个反向传播计算的计算图。

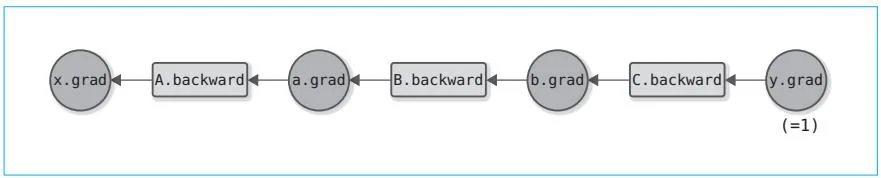
图6-2 反向传播的计算图

从图6-2可以看出各个函数的backward方法的调用顺序，也能看出应该将backward方法的结果赋给哪个变量的grad。下面是反向传播的实现。

steps/step06.py

y.grad = np.array(1,0)  
b.grad = C.backward(y.grad)  
a.grad = B_backward(b.grad)  
x.grad = A_backward(a.grad)  
print(x.grad)

运行结果

3.297442541400256

反向传播从 $\frac{\mathrm{dy}}{\mathrm{dy}} = 1$ 开始。因此，我们将输出y的导数设为np.array(1.0)。之后，只要按照C→B→A的顺序调用backward方法即可。这样就可以对各变量求出导数。

运行上面的代码后，得到的x.gradle的结果是3.297442541400256。这就是y对x的导数。顺带一提，步骤4的数值微分的结果是3.2974426293330694，这两个结果几乎一样。这说明反向传播的实现是正确的，更准确地说，这个实现大概率是正确的。

这样就完成了反向传播的实现。虽然我们得到了正确的运行结果，但是反向传播的顺序 $C \rightarrow B \rightarrow A$ 是通过编码手动指定的。在下一个步骤，我们会把这项工作自动化。

步骤7

反向传播的自动化

在上一个步骤中，我们实现的反向传播成功运行。但是，我们不得不手动编写进行反向传播计算的代码。这就意味着每次进行新的计算时，都得编写这部分代码。比如在图7-1所示的情况下，我们必须为每个计算图编写反向传播的代码。这样不但容易出错，还浪费时间，所以我们让Python来做这些无聊的事情吧。

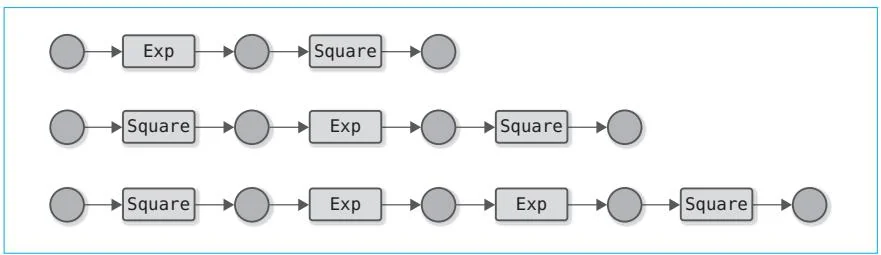
图7-1 各种计算图的例子（变量名省略，函数用类名表示）

接下来要做的就是让反向传播自动化。准确来说，就是要建立这样一个机制：无论普通的计算流程(正向传播)中是什么样的计算，反向传播都能自动进行。我们马上要接触到Define-by-Run的核心了。

Define-by-Run是在深度学习中进行计算时，在计算之间建立“连接”的机制。这种机制也称为动态计算图。关于Define-by-Run及其优点的详细信息，请阅读步骤24的专栏。

图7-1所示的计算图都是流水线式的计算。因此，只要以列表的形式记录函数的顺序，就可以通过反向回溯自动进行反向传播。不过，对于有分支的计算图或多次使用同一个变量的复杂计算图，只借助简单的列表就不能奏效了。我们接下来的目标是建立一个不管计算图多么复杂，都能自动进行反向传播的机制。

其实只要在列表的数据结构上想想办法，将所做的计算添加到列表中，或许可以对任意的计算图准确地进行反向传播。这种数据结构叫作Wengert列表（也叫tape）。本书不对Wengert列表进行说明，感兴趣的读者请阅读参考文献[2]和参考文献[3]等。另外，关于借助Wengert列表实现Define-by-Run的优点，请阅读参考文献[4]等。