58.1 VGG16的实现

VGG(参考文献[36])是在2014年的ILSVRC比赛中获得亚军的模型。在参考文献[36]中的文章中，作者通过改变模型中使用的层数等方式提出了几种变体，这里我们将实现其中一个名为VGG16的模型，其网络构成如图58-1所示。

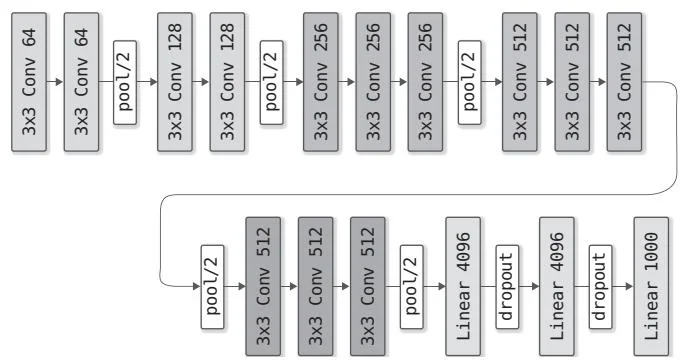
图58-1 VGG16的网络构成（图中省略了激活函数ReLU）

图58-1中的“ $3 \times 3$ conv 64”表示卷积核大小为 $3 \times 3$ ，输出通道数为64。另外，“pool/2”表示 $2 \times 2$ 的池化，“linear 4096”表示输出大小为4096的全连接层。VGG16有以下几个特点。

• 使用 $3 \times 3$ 的卷积层（填充为 $1 \times 1$ ）

• 卷积层的通道数量（基本上）在每次池化后变为原来的2倍 $(64 \rightarrow 128 \rightarrow 256 \rightarrow 512)$

• 在全连接层使用Dropout

• 使用ReLU作为激活函数

现在参照图58-1来实现VGG16。代码如下所示

dezero/models.py

importdezero-functionsasF   
importdezero.layersasL   
classVGG16(Model): def__init__(self): super(）.__init_（） #  $①$  只指定输出的通道数 self.conv1_1  $=$  L.Conv2d(64,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv1_2  $=$  L.Conv2d(64,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv2_1  $=$  L.Conv2d(128,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv2_2  $=$  L.Conv2d(128,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv3_1  $=$  L.Conv2d(256,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv3_2  $=$  L.Conv2d(256,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv3_3  $=$  L.Conv2d(256,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv4_1  $=$  L.Conv2d(512,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv4_2  $=$  L.Conv2d(512,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv4_3  $=$  L.Conv2d(512,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv5_1  $=$  L.Conv2d(512,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv5_2  $=$  L.Conv2d(512,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.conv5_3  $=$  L.Conv2d(512,kernel_size=3,stride  $= 1$  pad  $= 1$  ) self.fc6  $\equiv$  L.Linear(4096）#  $②$  只指定输出的大小 self.fc7  $\equiv$  L.Linear(4096) self.fc8  $\equiv$  L.Linear(1000) defforward(self,x):  $\mathbf{x} = \mathbf{F}$  .relu(self.conv1_1(x))  $\mathbf{x} = \mathbf{F}$  .relu(self.conv1_2(x))

$\begin{array}{rl} & {\mathrm{x} = \mathrm{F}.p o o l i n g(\mathrm{x},2,2)}\\ & {\mathrm{x} = \mathrm{F}.r e l u(\mathrm{s}f.\mathrm{e}v_{\mathrm{l}}.\mathrm{c}o v_{\mathrm{2\_1}}(\mathrm{x}))}\\ & {\mathrm{x} = \mathrm{F}.r e l u(\mathrm{s}f.\mathrm{e}v_{\mathrm{l}}.\mathrm{c}o v_{\mathrm{2\_2}}(\mathrm{x}))}\\ & {\mathrm{x} = \mathrm{F}.p o o l i n g(\mathrm{x},2,2)}\\ & {\mathrm{x} = \mathrm{F}.r e l u(\mathrm{s}f.\mathrm{e}v_{\mathrm{l}}.\mathrm{c}o v_{\mathrm{3\_1}}(\mathrm{x}))}\\ & {\mathrm{x} = \mathrm{F}.r e l u(\mathrm{s}f.\mathrm{e}v_{\mathrm{l}}.\mathrm{c}o v_{\mathrm{3\_2}}(\mathrm{x}))}\\ & {\mathrm{x} = \mathrm{F}.r e l u(\mathrm{s}f.\mathrm{e}v_{\mathrm{l}}.\mathrm{c}o v_{\mathrm{3\_3}}(\mathrm{x}))}\\ & {\mathrm{x} = \mathrm{F}.p o o l i n g(\mathrm{x},2,2)}\\ & {\mathrm{x} = \mathrm{F}.r e l u(\mathrm{s}f.\mathrm{e}v_{\mathrm{l}}.\mathrm{c}o v_{\mathrm{4\_1}}(\mathrm{x}))}\\ & {\mathrm{x} = \mathrm{F}.r e l u(\mathrm{s}f.\mathrm{e}v_{\mathrm{l}}.\mathrm{c}o v_{\mathrm{4\_2}}(\mathrm{x}))}\\ & {\mathrm{x} = \mathrm{F}.r e l u(\mathrm{s}f.\mathrm{e}v_{\mathrm{l}}.\mathrm{c}o v_{\mathrm{4\_3}}(\mathrm{x}))}\\ & {\mathrm{x} = \mathrm{F}.p o o l i n g(\mathrm{x},2,2)}\\ & {\mathrm{x} = \mathrm{F}.r e s h a p e(\mathrm{x},(\mathrm{x}.s h a p e[\theta ], - 1))}\end{array}$  #  $③$  变形  
x=F.dropout(F.relu(self.fc6(x)))  
x=F.dropout(F.relu(self.fc7(x)))  
x= self.fc8(x)  
return x

代码很长，但结构很简单。初始化方法创建需要的层，forward方法使用层和函数来进行处理。接下来补充说明上面代码中标记的3处。

首先①处在创建卷积层时没有指定输入数据的通道数。输入数据的通道数是从正向传播的数据流中获得的，同时权重参数也会被初始化。②处的L.Linear(4096)同样只指定了输出大小。输入的大小是由实际流入的数据自动确定的，所以②处只指定输出大小即可。

最后③处为了从卷积层切换到全连接层对数据进行了变形。卷积层处理的是四阶张量，全连接层处理的是二阶张量。因此，在向全连接层传播数据之前，要使用reshape函数将数据变形为二阶张量。以上就是VGG16类的实现。