56.2 结合方块进行思考

如果把三阶张量看作方块，就容易理解它的卷积运算了。如图56-2所示，笔者结合三维的方块来介绍三阶张量。

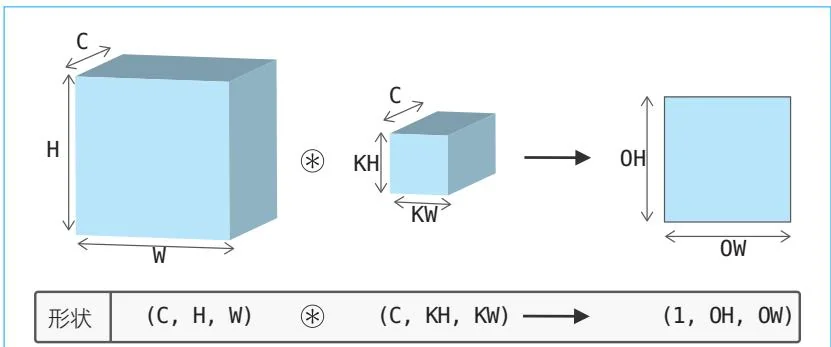
图56-2 结合方块来思考卷积运算

图56-2中数据的书写顺序是(channel, height, width)。例如，通道数为C、高度为H、宽度为W的数据的形状可写为(C, H, W)。过滤器的情况也一样，按照(channel, height, width)的顺序书写即可。如果通道数为C、过滤器的

高度为 $\mathrm{KH}^{①}$ ，宽度为KW，则写为（C，KH，KW）。

输出被称为“特征图”。在图56-2的例子中，输出以一个特征图的形式显示出来。假设我们想让通道方向上有多个特征图。要达到这样的效果，需要用到多个过滤器(权重)。具体如图56-3所示。

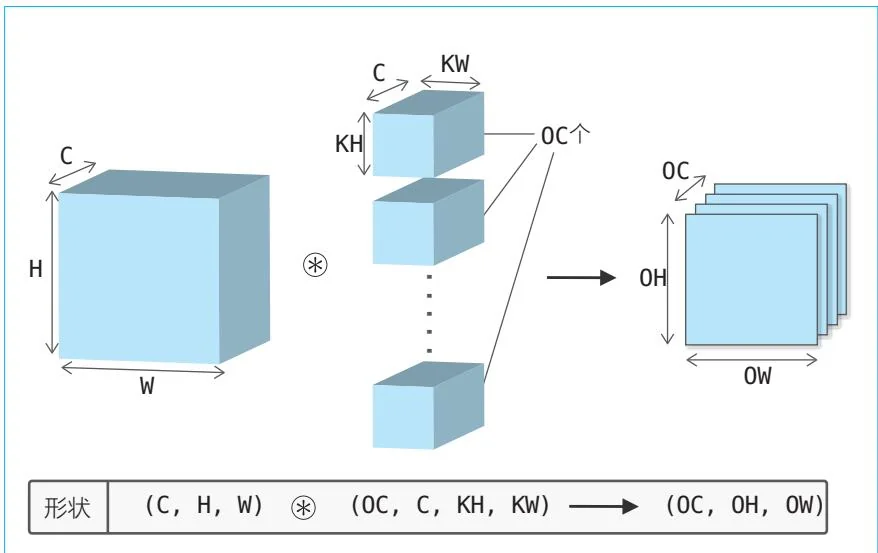
图56-3 基于多个过滤器的卷积运算的例子

图56-3中的各张量分别应用了OC②个过滤器。于是有OC个特征图会被创建出来。这OC个特征图汇总在一起就是(OC，OH，OW)形状的方块。

从图56-3可以看出，关于卷积运算的过滤器，其数量也是我们需要考虑的要素。为此，我们要把过滤器的权重数据设为一个四阶张量，将其数据形状规定为(output_channel，input_channel，height，width)。如果有20个通道数为3、大小为(5,5)的过滤器，那么该过滤器的形状为(20,3,5,5)。

卷积运算中(和全连接层相同)也存在偏置。图56-4在图56-3的基础上添加了偏置的加法处理。

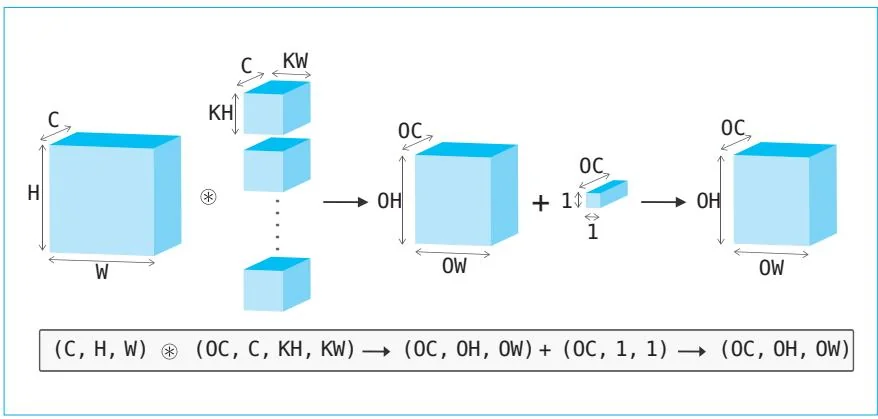
图56-4 卷积运算的处理流程（又添加了偏置项）

如图56-4所示，每个通道只有一个偏置。这里，偏置的形状是(OC，1，1)，应用过滤器后的输出的形状是(OC，OH，OW)。由于形状不同，偏置在被广播处理之后加到结果中。以上就是包含了偏置加法运算的卷积运算。