37.2 使用张量时的反向传播

这是本步骤的核心内容。此前在反向传播的实现中，我们一直是以标量为对象的。那么对使用了张量的计算进行反向传播，会发生什么呢？其实在使用当前已实现函数的情况下，即使对张量进行计算，反向传播的代码也能正常工作，理由如下。

• 我们以标量为对象实现了反向传播

• 向目前实现的DeZero函数传入张量，函数会将每个张量的元素作为标量进行计算

• 如果将张量的每个元素作为标量进行计算，那么以标量为前提实现的反向传播也会对张量的每个元素进行计算

从上面的推导过程可知，对逐元素进行计算的DeZero函数来说，即使传入的是张量，反向传播也能正常工作。实际验证的结果如下。

steps/step37.py

$\begin{array}{rl} & {\mathrm{x} = \mathrm{Variable}(\mathrm{np.array}([1,2,3],[4,5,6])})}\\ & {\mathrm{c} = \mathrm{variable}(\mathrm{np.array}([10,20,30],[40,50,60]))}\\ & {\mathrm{t} = \mathrm{x} + \mathrm{c}}\\ & {\mathrm{y} = \mathrm{F-sum}(t)} \end{array}$

上面的代码使用了用于求和的sum函数进行计算。sum函数会在步骤39中实现，这里提前使用了它。sum函数会对传入的张量求其元素之和，然后输出一个标量。上面代码中的x、c、t，其形状都是(2,3)，只有最后的输出y是标量。

机器学习的问题中通常会设置一个以张量为输入，但以标量为输出的函数（损失函数）。上面的代码假定了机器学习问题的场景，最后进行了输出标量的计算。

前面代码中所做的计算可以用图37-1所示的计算图表示。

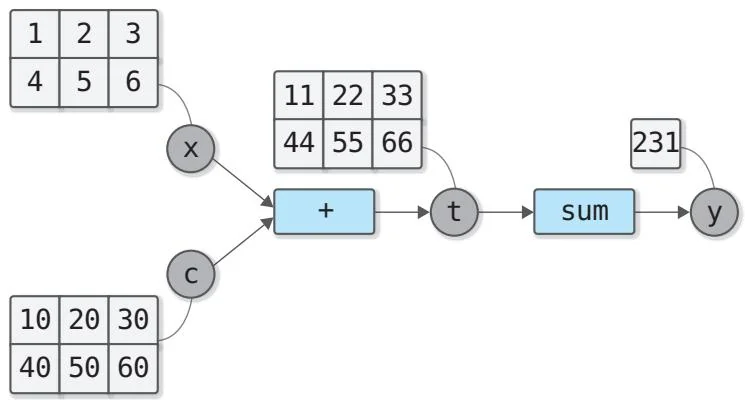
图37-1 使用张量的计算图

图37-1具体展示了每个变量的数据。从图中可以看出最后的输出是标量。这里对这个最后的输出为标量的计算图进行反向传播。我们紧接着上面的代码编写如下代码。

steps/step37.py

y.backup(ret_grad=True)  
print(y.grad)  
print(t.grad)  
print(x.grad)  
print(c.grad)

运行结果

variable(1)  
variable([[1 1 1]  
[1 1 1]])  
variable([[1 1 1]  
[1 1 1]])  
variable([[1 1 1]  
[1 1 1]])

上面的代码调用了y backward(ret_grad=True)求各变量的导数。代码

中使用参数 retain_grad=True 保留了所有变量的导数，输出的结果也是正确的。正如这段代码所展示的那样，当前的 DeZero 函数使用张量也能正确地进行反向传播。

这里有一点很重要，即梯度的形状和数据的形状（正向传播过程中的数据）必须一致。这意味着x.shape == x.grad.shape、c.shape == c.grad.shape、t.shape == t.grad.shape。利用这个特性，我们有望实现那些不是逐元素计算的函数，如sum和reshape等，这部分内容会在下一个步骤实现reshape函数时介绍。

张量的导数在机器学习领域称为梯度，Variable类的grad其实是gradient(梯度)的缩写。从现在开始，本书将不再使用“张量的导数”这一叫法，而是将其称为“梯度”。

以上就是本步骤的主要内容。最后通过式子来补充说明使用张量时的反向传播。补充的内容有些难度，但与后续步骤的关联不大，所以跳过这部分内容也没有问题。

37.3 使用张量时的反向传播（补充内容）

本节使用式子来说明使用张量时的反向传播。首先是事先准备。思考函数 $\pmb{y} = F(\pmb{x})$ ，其中 $\pmb{x}$ 和 $\pmb{y}$ 是向量，假设这两个向量的元素数都是 $n$ 。

这里只讨论向量的情况，但是本节得出的结论(理论)也适用于张量（ $n$ 阶张量）的情况。这是因为在使用张量进行计算的情况下，只要增加向量化过程(将元素排成一列，变形为向量的处理)作为预处理即可。于是，这里的向量理论就可以直接应用于张量了。

我们来看看 $\pmb{y} = F(\pmb{x})$ 的导数。 $\pmb{y}$ 对 $\pmb{x}$ 的导数可通过以下式子定义。

由于 $y$ 和 $x$ 都是向量，所以导数为上面这种矩阵形式。这个矩阵也叫雅可比矩阵。顺带一提，如果 $y$ 不是向量而是标量，那么 $y$ 对 $x$ 的导数就是下面这样。

这是一个 $1 \times n$ 的雅可比矩阵，我们可以将它看作一个行向量（=水平向量）。

接下来思考复合函数。假设有复合函数 $y = F(x)$ ，它由3个函数复合而成，分别是 $a = A(x)$ ， $b = B(a)$ ， $y = C(b)$ 。假设变量 $x$ 、 $a$ 、 $b$ 都是向量，它们的元素数为 $n$ ，只有最终的输出 $y$ 是标量。那么，基于链式法则， $y$ 对 $x$ 的导数可以表示如下。

式子37.1是基于链式法则得出的结果，其中的 $\frac{\partial y}{\partial b}$ 和 $\frac{\partial b}{\partial a}$ 表示雅可比矩阵。将它们作为矩阵的乘积进行计算（步骤41中会介绍矩阵的乘积），这就是式子37.1表示的内容。

接下来思考式子37.1中矩阵的乘积的计算顺序。有两种计算方法，第一种是图37-2那种从输入端到输出端的计算方式。

图37-2所示的这种沿输入端到输出端的方向添加括号的方法叫作自动微分的前向模式(下文简称为前向模式)。这里要注意的一点是，中间的矩阵乘积结果是矩阵。例如 $\frac{\partial b}{\partial a}\frac{\partial a}{\partial x}$ 的结果是一个 $n\times n$ 矩阵。

另一种方法是沿输出端到输入端的方向添加括号进行计算，具体如图37-3所示。这就是反向模式（准确来说是自动微分的反向模式）。

图37-3展示了沿输出端到输入端的方向添加括号进行计算的方法。这时由于 $y$ 是标量，所以中间的矩阵乘积结果都是向量(行向量)。例如， $\frac{\partial y}{\partial b}\frac{\partial b}{\partial a}$ 的结果是一个由 $n$ 个元素组成的向量。

图37-2 沿输入端到输出端的方向添加括号（前向模式）
图37-3 沿输出端到输入端的方向添加括号（反向模式）

前向模式下传播的是 $n \times n$ 矩阵，而反向模式下传播的是有 $n$ 个元素的向量。另外，向量和矩阵的乘积的计算成本比矩阵和矩阵的乘积的计算成本更低。基于这些原因可知反向模式，也就是反向传播在计算方面更加高效。

如图37-3所示，反向模式(在式子上)由向量和雅可比矩阵的乘积组成。以图37-3为例，首先求 $\frac{\partial y}{\partial b}$ （向量)和 $\frac{\partial b}{\partial a}$ （雅可比矩阵)的积，然后求 $\frac{\partial y}{\partial a}$ （向量）和 $\frac{\partial a}{\partial x}$ （雅可比矩阵)的积。像这样，反向传播中会针对每个函数求向量和雅可比矩阵的乘积。

需要注意的是，我们不必特意先求出雅可比矩阵再计算矩阵的乘积，只要求出结果就可以进行反向传播了。举例来说，我们思考一下图37-3中的 $\pmb{a} = A(\pmb{x})$ 逐元素进行计算的场景(比如 $\pmb{a} = \sin (\pmb{x})$ )。如果求这个函数的雅可比矩阵，可得以下结果。

通过上式可知，在逐元素计算的情况下，函数的雅可比矩阵是对角矩阵（对角矩阵是主对角线之外的元素皆为0的矩阵）。其原因是 $x_{i}$ 只影响 $a_{i}(i$ 是 $1\sim n$ 的整数)。在雅可比矩阵是对角矩阵的情况下，向量和雅可比矩阵的乘积如下所示。

从上面的式子可以看出，最终的结果可以通过求各元素的导数，然后将导数乘以各个元素来求出。也就是说，在逐元素计算的情况下，我们也可以通过拿导数乘以每个元素的方式来求出反向传播。

这种计算方式的重点是，我们不必特意先求出雅可比矩阵再计算矩阵的乘积，只要求出结果即可。因此，如果有更高效的计算(实现)方法，我们就可以使用这种计算方式。

以上就是通过式子介绍的张量版反向传播的内容。

步骤38

改变形状的函数

上一个步骤介绍了对张量进行计算时的反向传播。以下是我们学到的内容。

• 对于逐元素进行计算的函数，如add函数和sin函数，我们可以假定输入和输出是标量，以此为前提实现正向传播和反向传播

• 在这种情况下，即使输入是张量，反向传播也是有效的

接下来我们要看的是不会逐元素进行计算的函数。首先，我们要实现两个函数：一个是改变张量形状的reshape函数，另一个是执行矩阵转置的transpose函数。这两个函数都会改变张量的形状。