30.3 确认工作③：Variable类的反向传播

最后来看看反向传播的逻辑。Variable类的backward方法实现了反向传播。这里我们来看看如下所示的Variable类的backward方法，重点关注阴影部分。

class Variable: def backward(self, retain_grad=False): if self.grad is None: self.grad = np.ones_like(self.data) funcs  $=$  [] seen_set  $\equiv$  set() def add_func(f): if f not in seen_set: funcs.append(f) seen_set.add(f) funcs.sort(key=lambda x:x_generation) add_func(self creator) while funcs: f  $=$  funcs.pop() #反向传播的计算(主处理） gys  $=$  [output().grad for output in f.outputs] #  $①$  gxs  $=$  f.backup(*gys)#  $②$  if not isinstance(gxs,tuple): gxs  $=$  (gxs,) forx,gx in zip(finputs,gxs): #  $③$  if x.grad is None: x.grad  $\equiv$  gx else: x.grad  $\equiv$  x.grad +gx

if x creator is not None: add_func(x creator) if not retain_grad: for y in f.outputs: y().grad = None

① 的部分将Variable的实例变量grad汇总在列表中。这里的实例变量grad引用了ndarray实例。因此，元素为ndarray实例的列表传给了②处的backward方法。③的部分把从输出端开始传播的导数(gxs)设置为函数的输入变量(finputs)的grad。

根据以上内容，我们一起来看看下面这段代码。

$\mathbf{x} =$  Variable(np.array(1.0))  
y  $=$  sin(x)  
y.backup(retain_grad=True)

上面的代码进行了sin函数的计算(正向传播)，然后进行反向传播。这里使用了y backward(retain_grad=True)使所有变量保留导数(这个函数是在步骤18中为了改善性能引入的)。图30-4展示了此时变量和函数的“活动”可视化后的样子。

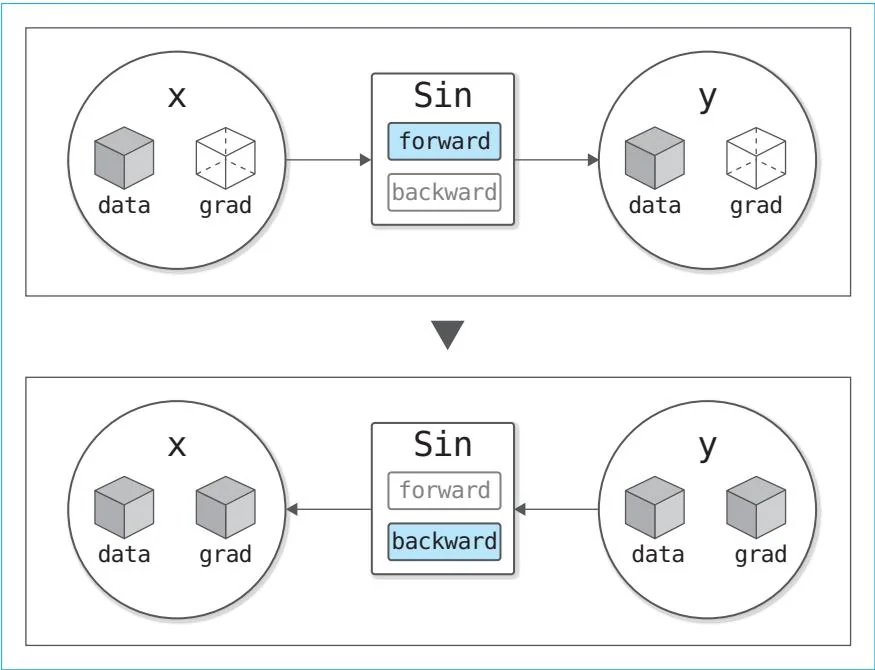
图30-4 y=sin(x)的计算图的正向传播和反向传播

如图30-4所示，执行计算 $y = \sin(x)$ 时，计算图被创建，Variable的实例变量data被赋值。通过反向传播，Sin类的backward方法被调用，Variable的实例变量grad被赋值。

这就是目前DeZero的反向传播的实现方式。在下一个步骤中，我们将修改当前的DeZero，以求解高阶导数。

步骤31

高阶导数（理论篇）

在上一个步骤，我们回顾了DeZero目前的实现情况。主要内容可归纳为以下几点。

• 计算的连接是在Function类的__call__方法中创建的

• 正向传播和反向传播的具体计算是在继承了 Function 的类的 forward 方法和 backward 方法中进行的

这里要注意的是创建计算图连接的时机。连接是在进行正向传播的计算时创建的，在反向传播时不会被创建。这就是问题的关键所在。