29.2_使用牛顿法实现优化

29.2 使用牛顿法实现优化

下面来实现牛顿法。要使用牛顿法进行优化，只要实现式子29.5即可。不过DeZero无法自动计算二阶导数，所以我们要手动对其进行计算，具体如下。

y = x ^ {4} - 2 x ^ {2}

\frac {\partial y}{\partial x} = 4 x ^ {3} - 4 x

\frac {\partial^ {2} y}{\partial x ^ {2}} = 1 2 x ^ {2} - 4

基于以上结果，我们可以按如下方式使用牛顿法实现优化。

steps/step29.py

import numpy as np   
fromdezero import Variable   
deff(x):  $\mathrm{y} = \mathrm{x}^{**}\mathrm{4 - 2}^{*}\mathrm{x}^{**}\mathrm{2}$  return y   
defgx2(x): return  $12*x**2 - 4$ $\mathbf{x} =$  Variable(np.array(2.0))   
iters  $= 10$    
fori in range它是： print(i,x)  $\mathrm{y} = \mathrm{f}(\mathrm{x})$  x.cleargrad() y.backup() x.data  $- =$  x.grad/gx2(x.data)

与之前相同，一阶导数通过反向传播求得。二阶导数则通过手动编码求得。之后根据牛顿法的更新公式来更新 $x$ 。运行上面的代码，可以看到如下所示的 $\mathbf{x}$ 值的更新过程。

0 variable(2.0)  
1 variable(1.4545454545454546)  
2 variable(1.1510467893775467)  
3 variable(1.0253259289766978)  
4 variable(1.0009084519430513)  
5 variable(1.0000012353089454)  
6 variable(1.000000000002289)  
7 variable(1.0)  
8 variable(1.0)  
9 variable(1.0)

本题的答案(最小值)是1。从上面的结果可以看出，实际只迭代了7次就找到了最小值。与之相比，梯度下降法需要迭代很多次才能接近最优解。

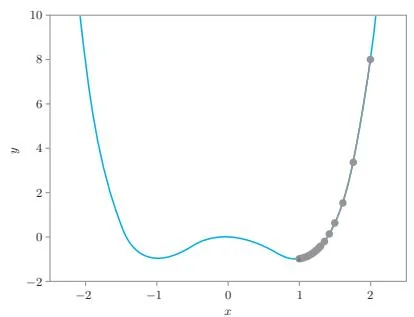
图29-5是两种方法的更新路径的比较图。

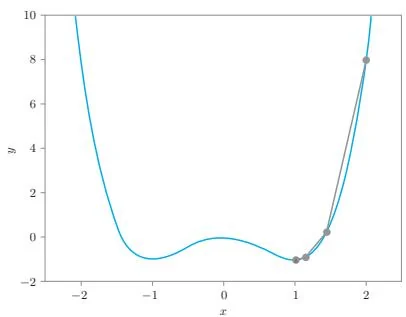
图29-5 梯度下降法（左）的更新路径和牛顿法（右）的更新路径

如图29-5所示，梯度下降法的迭代次数较多。上图中梯度下降法的结果是当学习率设置为0.01时的情况，此时要经过124次迭代， $x = 1.0$ 的绝对误差才小于0.001。相比之下，牛顿法只需迭代7次。

以上就是牛顿法的理论知识和实现。本步骤实现了牛顿法，并使用它解决了具体问题，取得了很好的效果。不过，在实现过程中，二阶导数的计算是手动进行的（为了求得二阶导数，要手动写出式子，并手动将其编写为代码）。接下来要做的就是将这个手动的过程自动化。

步骤30

高阶导数（准备篇）

当前的 DeZero 虽然实现了自动微分，但只能计算一阶导数。这里我们来扩展 DeZero，使它能自动计算二阶导数，甚至是三阶导数、四阶导数等高阶导数。

要想使用DeZero求二阶导数，我们需要重新思考目前反向传播的实现方式。DeZero的反向传播是基于Variable类和Function类实现的。我们先来简单回顾一下目前Variable和Function这两个类的实现。由于内容较多，所以笔者分3节来进行介绍。