42.3 线性回归的实现

下面使用DeZero实现线性回归。这里将代码分为前后两部分。首先展示代码的前半部分。

steps/step42.py

import numpy as np   
fromdezero import Variable   
importdezero-functionsasF   
#玩具数据集   
np.random.seed(0)   
 $\mathrm{x} = \mathrm{np}$  .random RAND(100,1)   
 $y = 5 + 2*x + np$  .random rand(100,1)   
x，y  $=$  Variable(x)，Variable(y） #可以省略   
W=Variable(np.zeros((1,1)))   
b  $=$  Variable(np.zeros(1))   
def predict(x): y  $=$  F.matmul(x,W)+b return y

上面代码中创建的参数W和b是Variable实例(W为大写字母)。至于二者的形状，W为(1,1)，b为(1,)。

DeZero函数可以直接处理ndarray实例(这些实例会在DeZero内部被转换为Variable实例)。因此，上面代码中的数据集x和y可以作为ndarray实例处理，无须显式地转换为Variable实例。

上面的代码还定义了predict函数，这个函数使用matmul函数进行计算。我们可以使用矩阵的乘积一次性对多个数据（在上面的例子中是100个数据）进行计算。这时，形状的变化如图42-3所示。

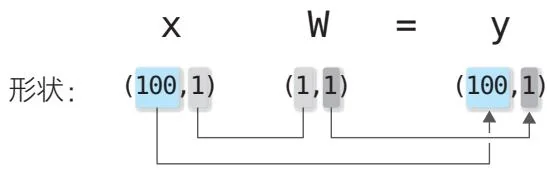
图42-3 矩阵乘积的形状的变化（这里没有加上b）

从图42-3可以看出，相应维度的元素数量是相同的。得到的结果y的形状是(100，1)。换言之，拥有100个数据的x中的所有数据都分别与W相乘了。这样我们就能在一次计算中得到所有数据的预测值。这里x的数据维度是1，即使维度为D，只要将W的形状设置为(D，1)，依然能进行正确的计算。例如当D=4时，矩阵乘积的计算如图42-4所示。

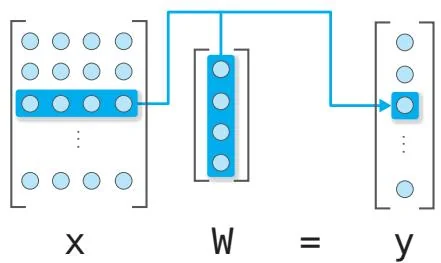
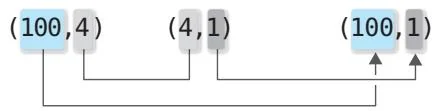
图42-4 矩阵乘积的形状的变化（当x数据的维度为4时）

如图 42-4 所示, 让 x.shape[1] 和 W.shape[0] 相同后, 矩阵乘积的计算就

能正确进行。在这种情况下，100个数据中的每一个数据都将与W进行向量内积的计算。

上面代码中的 $y = F$ .matmul(x, W) + b在计算过程中会进行一次广播。具体来说，b的形状是(1，)，在元素被复制成(100，1)的形状后，程序对每个元素进行加法运算。我们已在步骤40支持了广播。因此在广播的情况下，反向传播也会正确进行。

接下来是代码的后半部分，如下所示。

steps/step42.py

def mean_squared_error(x0, x1):
    diff = x0 - x1
    return F.sum(diff ** 2) / len(diff)
lr = 0.1
iters = 100
for i in range(iters):
    y_pred = predict(x)
    loss = mean_squared_error(y, y_pred)
    W.cleargrad()
    b.cleargrad()
    loss/backward()
    W.data -= lr * W.grad.data
    b.data -= lr * b.grad.data
print(W, b, loss)

上面的代码实现了求均方误差的函数mean_squared_error(x0, x1)。函数内部只是使用DeZero函数对式子42.1进行了实现。下一步是通过梯度下降法更新参数，相关实现已经在步骤28中完成了。这里需要注意的是，更新参数的计算是像W.data == lr * W.grad.data这样在实例变量data上进行的。参数的更新只是简单地对数据进行更新，因此不需要创建计算图。

运行上面的代码，从结果可以看出，损失函数的输出值是逐渐减少的。

最后得到的值是 $W = \left[ \begin{array}{ll} 2.11807369 \end{array} \right]$ ， $b = \left[ \begin{array}{ll} 5.46608905 \end{array} \right]$ 。作为参考，这里给出根据这些参数得到的图形，具体如图42-5所示。

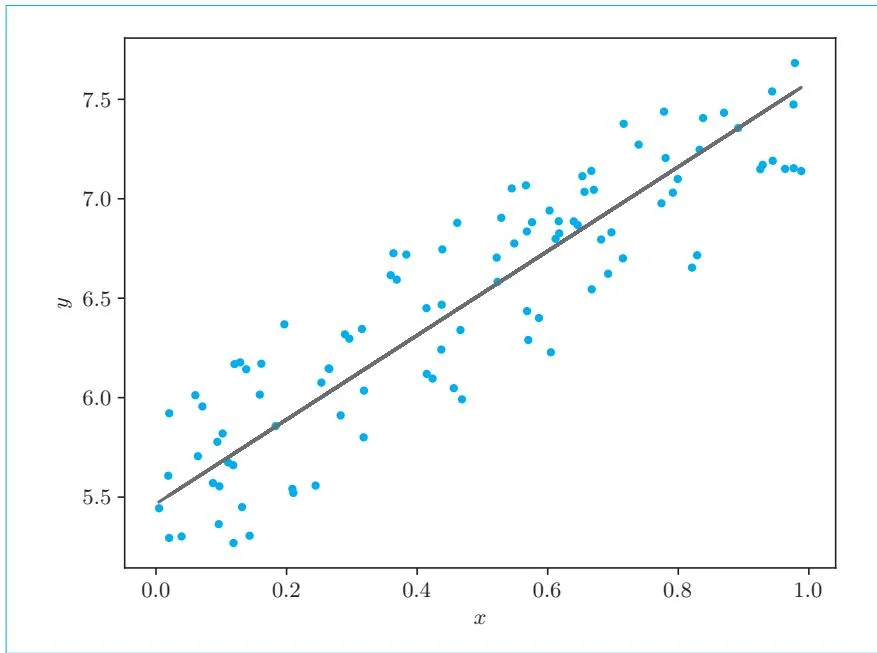
图42-5 训练后的模型

如图42-5所示，我们已经得到了一个拟合数据的模型。我们使用DeZero正确实现了线性回归。以上就是线性回归的实现。最后，笔者对DeZero的mean_squared_error函数进行补充说明。

42.3_线性回归的实现

42.3 线性回归的实现