24.3 Goldstein-Price函数

Goldstein-Price函数可用以下式子表示。

\begin{array}{l} \left[ 1 + (x + y + 1) ^ {2} \left(1 9 - 1 4 x + 3 x ^ {2} - 1 4 y + 6 x y + 3 y ^ {2}\right) \right] \\ \left[ 3 0 + (2 x - 3 y) ^ {2} \left(1 8 - 3 2 x + 1 2 x ^ {2} + 4 8 y - 3 6 x y + 2 7 y ^ {2}\right) \right] \\ \end{array}

看起来很复杂，但有了DeZero，编码就没有那么难了。实际编写的代码如下所示。

steps/step24.py

def goldstein(x, y):
    z = (1 + (x + y + 1)**2 * (19 - 14*x + 3*x**2 - 14*y + 6*x*y + 3*y**2)) * (30 + (2*x - 3*y)**2 * (18 - 32*x + 12*x**2 + 48*y - 36*x*y + 27*y**2))
    return z

对照式子可以很快完成编码。对普通人来说，不使用运算符是写不出这个函数的代码的。下面尝试计算Goldstein-Price函数的导数。

steps/step24.py

$\mathbf{x} =$  Variable(np.array(1.0))   
y  $=$  Variable(np.array(1.0))   
z  $=$  goldstein(x,y)   
z.backup()   
print(x.grad，y.grad)

运行结果

-5376.0 8064.0

运行上面的代码，可得到x的导数为-5376.0，y的导数为8064.0。这些都是正确的结果。就连Goldstein-Price函数这样复杂的计算，DeZero都能求出它的导数。大家可以通过梯度检验来验证结果是否正确。以上就是第2阶段的内容。

★★★★★★★★

在第2阶段，DeZero已经有了很大的进步。在这个阶段刚开始的时候，DeZero只能进行简单的计算，现在它已经可以进行复杂的计算了（准确来说，无论计算图的“连接”多么复杂，它都可以正确地进行反向传播）。另外，通过重载运算符，我们可以像编写普通的Python程序一样编写代码。从能够自动微分的角度来看，DeZero可以说是把普通编程变成了可微分编程(differentiable programming)。

DeZero的基础部分到这里就完成了。在下一个阶段，我们将扩展DeZero来进行更复杂的计算。

专栏：Define-by-Run

深度学习框架可以分为两大类：一类是基于Define-and-Run的框架，另一类是基于Define-by-Run的框架。本专栏将介绍这两种方式及其优缺点。

Define-and-Run（静态计算图）

Define-and-Run 可以直译为“定义计算图，然后流转数据”。用户定义计算图，然后由框架对计算图进行转换，这样就能流转数据。这个处理流程如图 B-1 所示。

图B-1 Define-and-Run式的框架的处理流程

如图B-1所示，框架转换了计算图的定义。方便起见，我们将这种转换操作称为编译。通过编译，框架将计算图加载到内存中，为数据流转做好准备。这里比较重要的一点是“计算图的定义”和“流转数据”的处理是分开的。查看下面的伪代码可以更清楚地了解这一点。

虚拟的Define-and-Run式框架的示例代码

计算图的定义

a = Variable('a')  
b = Variable('b')  
c = a * b  
d = c + Constant(1)

计算图的编译

$f =$  compile(d)

数据流转

$d = f(a = np.array(2), b = np.array(3))$

示例代码的前4行定义了计算图。需要注意的是，这4行代码并没有实际进行计算。所以，编程的对象是“符号”，而不是“数值”。顺带一提，这种编程叫作符号式编程（symbolic programming）。

如前面的代码所示，在Define-and-Run式的框架中，用户需要对使用了符号的抽象计算过程(而不是实际的数据)进行编码，而且这些代码必须用领域特定语言来编写。这里所说的领域特定语言是一种由框架自身规则组成的语言。拿上面的例子来说，用户需要遵循“在Constant中存储常量”等规则。此外，如果想使用if语句进行切换操作，则需要通过特殊的操作来实现，这也是领域特定语言的规则。顺带一提，TensorFlow框架使用tf cond操作实现了if语句。下面是一个具体的例子。

import tensorflow as tf  
flg = tfagna(dtype=tf(bool)  
x0 = tfagna(dtype=tf.float32)  
x1 = tfagna(dtype=tf.float32)  
y = tf cond(flg, lambda: x0 + x1, lambda: x0 * x1)

如代码所示，TensorFlow为存储数据的tf placeholder(容器)创建了计算图。上面的代码使用tf cond操作根据运行时的flg的值来切换处理。换言之，

TensorFlow通过tf cond操作实现了Python的if语句。

许多 Define-and-Run 式框架使用领域特定语言来定义计算。领域特定语言换个说法就是运行在 Python 上的“新编程语言”（考虑到它们有自己的 if 语句和 for 语句等流程控制指令，称其为“新编程语言”比较合适）。领域特定语言也是用来求导的语言。在这样的背景下，近来深度学习框架也被称为可微分编程。

以上是对Define-and-Run的简单介绍。在深度学习早期，大部分框架可归类于Define-and-Run。其中比较有代表性的框架有TensorFlow、Caffe、CNTK等(TensorFlow后来也采用了Define-by-Run方式)。作为Define-and-Run的下一代出场的是Define-by-Run，我们的DeZero也采用了这种方式。

Define-by-Run（动态计算图）

Define-by-Run一词的意思是计算图是由数据流定义的。它的特点是“数据的流转”和“计算图的构建”同时进行。

以 DeZero 为例，当用户流转数据，即进行普通的数值计算时，DeZero 会在幕后创建为计算图准备的链接（引用）。这个链接就相当于 DeZero 中的计算图，它的数据结构是链表（linked list）。使用链表，就可以在计算结束后反向回溯链接。

使用Define-by-Run式的框架，用户就可以像使用NumPy编写普通程序一样编写代码。实际使用DeZero，我们可编写出以下代码。

import numpy as np   
fromdezero import Variable   
a  $=$  Variable(np.ones(10))   
b  $=$  Variable(np.ones(10)\*2)   
c  $=$  b\*a   
d  $= \mathrm{c} + 1$    
print(d)

上面的代码与使用NumPy的普通程序几乎完全相同。唯一不同的是，上面代码中NumPy的数据被封装在Variable类中。当代码执行时，代码中的值会立即被求出。DeZero在幕后为计算图创建了连接。

Chainer在2015年首次提出Define-by-Run范式。此后，它被PyTorch、MXNet、DyNet和TensorFlow(2.0版以后默认采用该方式)等许多框架采用。

动态计算图的优点

在使用动态计算图框架的情况下，我们可以像使用NumPy进行普通编程一样进行数值计算，这样就不用学习框架专用的领域特定语言了。另外，计算图也无须通过编译变为独有的数据结构。换言之，计算图可以像普通的Python程序一样被构建和执行。因此，用户可以使用Python的if语句和for语句构建计算图。实际使用DeZero可编写出以下代码。

$\mathbf{x} =$  Variable(np.array(3.0))   
y  $=$  Variable(np.array(0.0))   
while True:  $\mathrm{y} = \mathrm{y} + \mathrm{x}$  if y.data  $>100$  .. break   
y.backup()

如上所示，用户可以使用while语句和if语句来进行计算。计算图(在DeZero框架下相当于计算图的链接)在幕后被创建。上面的代码使用了while语句和if语句，其他的Python编程技术，如闭包和递归调用等也可以继续在DeZero框架下使用。

静态计算图(Define-and-Run)的框架需要在流转数据之前定义计算图。因此在数据流转的过程中，计算图的结构不能改变。另外，在使用静态计算图框架时，程序员还必须学会领域特定语言的特殊运算语法，比如相当于if语句的tf cond。

在调试时我们也可以看到动态计算图的优点。由于计算图是作为Python程序运行的，所以对它的调试和对普通Python程序的调试一样。当然，我们也可以使用pdb等Python调试器。在使用静态计算图框架时，代码则被编译器转换为只有框架才能理解和执行的表现形式，Python(Python解释器)自然无法理解这种独特的表现形式。静态计算图之所以难调试，是因为“计算图的定义”和“数据流转”是分离的。在大多数情况下，问题(bug)是在“数据流转”的过程中被发现的，但问题多由“计算图的定义”引起。使用静态计算图时，问题的出现场所和根源地往往是分开的，这就导致用户很难找到问题出现的原因。

静态计算图的优点

静态计算图最大的优点是性能。优化计算图是提高性能的一种方法。优化计算图的具体做法是改造计算图的结构和换用效率高的运算方式。下面看一下图 B-2 所示的例子。

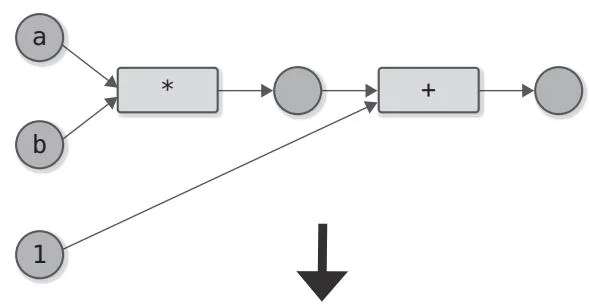
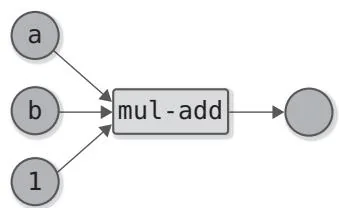
图B-2 计算图优化的示例

图B-2展示的是 $a * b + 1$ 的计算图和优化后的计算图。图中使用了一种可以同时进行乘法运算和加法运算的运算方式（大多数硬件有同时进行加法运算和乘法运算的指令）。由此，两个运算合并为一个运算，从而减少了计算时间。

除了上面这种细粒度的优化，我们还可以考虑对计算图的整体进行优化。由于在Define-and-Run式的框架中，整个计算图在数据流转前就已经存在了，所以对计算图整体进行优化是可行的。如果计算图中有通过for语句不断重复的运算，我们就可以将其合并起来，使运算变得更为高效。

神经网络的训练通常采用“只定义一次网络，多次在该网络中流转数据”的流程。在这种流程下，即使网络的构建和优化需要一定的时间，这些时间也很可能在反复流转数据的阶段节省下来。

Define-and-Run式框架的另一个优点是通过编译，计算图会转化为其他的运行形式。这样我们就可以在不借助Python的情况下流转数据。从Python中独立出来的最大好处是消除了Python带来的额外开销，这对计算资源匮乏的边缘计算环境来说尤为重要。

此外，在多台机器上执行分布式学习时，也有适用于Define-and-Run的情况。尤其是对计算图本身进行分割并将其分布到多台机器上的场景，在分割之前需要用到整个计算图。这就体现出Define-and-Run式框架的优点。

小结

上面讨论了Define-and-Run和Define-by-Run各自的优缺点，表B-1总结了这些内容。

表 B-1 比较静态计算图和动态计算图

如表B-1所示，两种模式各有利弊。简而言之，在性能方面，Define-and-Run更有优势；而在易用性方面，Define-by-Run具有显著优势。

此外，由于静态计算图和动态计算图各有利弊，所以许多框架兼备这两种模式。例如，PyTorch基本采用动态计算图的模式，但它也有静态计算图的模式（详见参考文献[16]）。同样，Chainer框架基本采用Define-by-Run，但它也可以切换为Define-and-Run的模式。TensorFlow从第2版开始将名为Eager Execution的动态计算图模式作为标配，它同样可以切换到静态计算图的模式。

最近，有人尝试在编程语言层面增加自动微分功能。其中一个著名的例子是Swift for TensorFlow（参考文献[17]）。这是对Swift这个通用编程语言的扩展，具体来说是修改Swift编译器，向其中加入自动微分机制。编程语言本身具备自动微分功能后，有望在性能和可用性两方面获得优势。

第3阶段

实现高阶导数

我们的DeZero现在已经能够完美地运行反向传播了。无论多么复杂的计算，它都能以正确的逻辑进行反向传播。有了现在的DeZero，许多需要求导的问题应该就能解决了。不过有些事情现在DeZero还做不到，比如计算高阶导数。

高阶导数指的是对导数求导数。具体来说，就是重复求导，从一阶导数到二阶导数，从二阶导数到三阶导数，以此类推。PyTorch和TensorFlow等现代深度学习框架都可以自动计算高阶导数。准确来说，它们可以在反向传播的基础上进一步进行反向传播（这个原理会在本阶段阐明）。

下面进入第3阶段。这个阶段的主要目标是扩展DeZero，使其能够计算高阶导数，DeZero的用途会由此变得更加广泛。我们继续前进吧！

步骤25

计算图的可视化（1）

现在的 DeZero 可以帮助我们轻松地将复杂的式子转化为代码。在步骤 24 中，我们已经编写了一个相当复杂的函数，即 Goldstein-Price 函数。如此复杂的计算背后会产生什么样的计算图呢？想必大家也想亲眼看看计算图的全貌吧。为此，本步骤将对计算图进行可视化操作。

对计算图进行可视化操作后，在问题发生的时候，我们会更容易找出问题出现的原因，有时还能发现更好的计算方法。让计算图可视化也是一种将神经网络的结构直观地传达给第三方的手段。

我们可以从头开始构建一个可视化工具，不过这就偏离深度学习的主题了。因此，本书选择使用第三方可视化工具Graphviz。在本步骤中，笔者主要介绍如何使用Graphviz，在下一个步骤，我们将使用Graphviz可视化计算图。

24.3_Goldstein-Price函数