43.4 神经网络的实现

通常，神经网络以“线性变换 $\rightarrow$ 激活函数 $\rightarrow$ 线性变换 $\rightarrow$ 激活函数 $\rightarrow$ 线性变换 $\rightarrow$ ……”的形式进行一系列的变换。例如，一个2层的神经网络可以用以下代码实现（这里省略了创建参数的代码）。

W1, b1 = Variable(...), Variable(...)
W2, b2 = Variable(...), Variable(...)
def predict(x):
    y = F.Linear(x, W1, b1) # 或者F LINEAR SIMPLE(...)
    y = F.sigmoid(y) # 或者F.SIGMID_SIMPLE(y)
    y = F.Linear(y, W2, b2)
    return y

上面的代码依次应用了线性变换和激活函数。这是用于神经网络推理

(predict)的代码。当然，为了正确地进行推理，训练是必不可少的。神经网络在训练过程中，会将损失函数加在推理处理的后面，然后找出使该损失函数的输出最小的参数。这就是神经网络的训练过程。

在神经网络中，线性变换或基于激活函数的变换称为层(layer)。此外，具有 $N$ 个执行线性变换的带有参数的层，能够连续进行变换的网络叫作“ $N$ 层神经网络”。

接下来使用实际的数据集来训练神经网络。代码如下所示

steps/step43.py

import numpy as np  
fromdezero import Variable  
importdezero-functionsasF

数据集

np.random.seed(0)  
x = np.random.randint(100, 1)  
y = np.sin(2 * np.pi * x) + np.random.randint(100, 1)

$①$ 权重的初始化

I, H, 0 = 1, 10, 1  
W1 = Variable(0.01 * np.random.randint(I, H))  
b1 = Variable(np.zeros(H))  
W2 = Variable(0.01 * np.random.randint(H, 0))  
b2 = Variable(np.zeros(0))

$②$ 神经网络的推理

def predict(x):
    y = F.Linear(x, W1, b1)
    y = F.sigmoid(y)
    y = F.Linear(y, W2, b2)
    return y
lr = 0.2
iters = 10000

$③$ 神经网络的训练

for i in range它是： y_pred  $=$  predict(x) loss  $=$  F.mean_squared_error(y,y_pred)

W1.cleargrad()  
b1.cleargrad()  
W2.cleargrad()  
b2.cleargrad()  
loss.backup()  
W1.data  $= \text{lr} * \text{W1Grad.data}$   
b1.data  $= \text{lr} * \text{b1Grad.data}$   
W2.data  $= \text{lr} * \text{W2Grad.data}$   
b2.data  $= \text{lr} * \text{b2Grad.data}$   
if i % 1000 == 0: # 每隔1000次输出一次信息  
print(loss)

上面的代码首先在①处初始化权重。这里的I(=1)对应于输入层的维度，H(=10)对应于隐藏层的维度，0(=1)对应于输出层的维度。根据此次处理的问题，我们要将I和0的值设置为1。H是超参数，它可以被设置为大于等于1的任何整数。另外，偏置被初始化为零向量(np.zeros(...))，权重被初始化为一个小的随机值(0.01 * np.random.randint(...))。

神经网络的权重的初始值需要设置为随机数。关于这样做的原因，请参阅《深度学习入门：基于Python的理论与实现》的6.2.1节。

②处的代码进行神经网络的推理，③处的代码用来更新参数。除参数增加了之外，③处的代码与上一个步骤的代码完全相同。

执行上面的代码后，神经网络就开始了训练。经过训练后的神经网络预测出了图43-4这样的曲线。

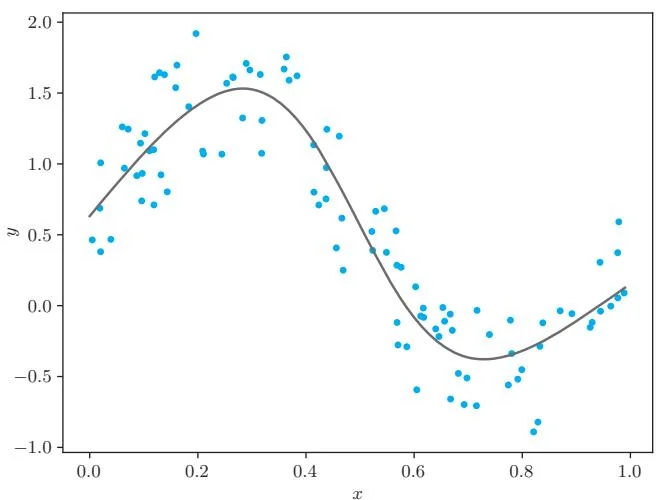
图43-4 训练后的神经网络

如图43-4所示，sin函数的曲线很好地拟合了数据。通过在线性回归的实现中叠加激活函数和线性变换，神经网络也能正确地学习非线性关系。

当然，我们还可以通过这种方式来实现由更深的层组成的神经网络。不过，随着层数的增加，参数的管理（重置参数的梯度和更新参数的工作）会变得更加复杂。在下一个步骤，我们将创建一个简化参数管理的机制。

步骤44

汇总参数的层

上一个步骤使用DeZero实现了神经网络。虽然简单，但它是一个真正的神经网络。现在我们可以说DeZero是一个神经网络框架了，不过它在易用性方面仍存在一些问题。接下来，我们将为DeZero增加更多神经网络的功能。这样可以使神经网络以及深度学习以更简单、更直观的方式实现。

本步骤要解决的问题是参数的处理。在上一个步骤，在重置参数的梯度（以及更新参数）时，我们不得不写一些相当枯燥的代码。后面我们将实现结构更加复杂的网络，到时参数处理将更加复杂。

参数是通过梯度下降等优化方法进行更新的变量。以上一个步骤为例，用于线性变换的权重和偏置就相当于参数。

本步骤将创建汇总参数的机制，为此我们将实现两个类：Parameter类和Layer类。使用这两个类可以实现参数的自动化管理。