43.1 DeZero中的linear函数

上一个步骤以简单的数据集为对象实现了线性回归。线性回归中（除了损失函数）只执行了矩阵乘积计算和加法运算。代码摘录如下。

上面的代码用来求输入 $x$ 和参数 $w$ 之间的矩阵乘积，然后加上 $b$ 的结果。这种变换叫作线性变换（linear transformation）或仿射变换（affine transformation）。

严格来说，线性变换指的是 $y = F$ .matmul(x, W)，其中不包括 b。在神经网络领域，人们通常把包括 b 的运算称为线性变换（本书也沿用此叫法）。另外，线性变换对应于神经网络中的全连接层，其中的参数 W 叫作权重 (weight)，参数 b 叫作偏置 (bias)。

这里我们将上述线性变换实现为 linear 函数。上一个步骤也提到过，实现方式有两种：一种是使用已经实现的 DeZero 函数；另一种是继承 Function 类，实现一个名为 Linear 的新函数类。前面已经说过，后者的内存效率更高。从图 43-1 中可以看出这一点。

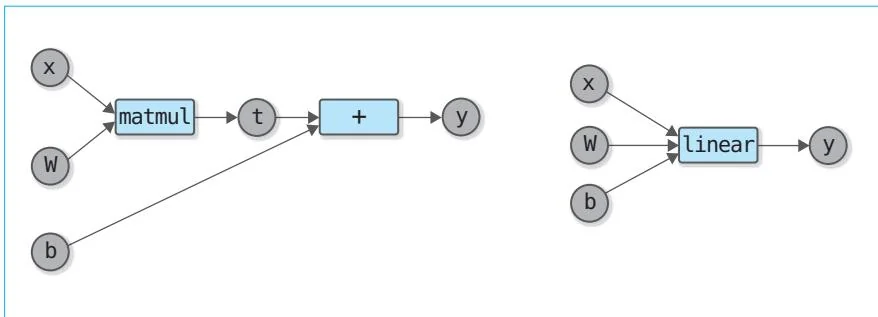
图43-1 线性变换的两种实现方式

图43-1左图的实现方式使用了DeZero的matmul函数和 $(\mathsf{add}$ 函数)。使用这种方式时，matmul函数的输出作为Variable实例记录在计算图中。也就是说，在计算图存在期间，Variable实例和它内部的数据(ndarray实例)会保存在内存中。

图43-1右图的实现方式是继承Function类后实现Linear类。由于在使用这种方式的情况下，中间结果没有作为Variable实例存储在内存中，所以正向传播中使用的数据在正向传播完成后会立即被删除。因此从内存效率的角度考虑，要想让第三方使用DeZero，我们需要使用第二种实现方式。不过针对第一种实现方式，有一个可以改善内存效率的技巧。下面笔者来介绍一下这个技巧。

再次观察图43-1的左图。matmul函数的输出变量是t。这个变量t是matmul函数的输出，也是+(add函数)的输入。现在思考一下这两个函数的反向传播。首先，+的反向传播仅仅传播输出端的梯度。也就是说，+的反向传播中不需要t的数据。另外，matmul的反向传播只需要输入变量x、W和b。因此，matmul的反向传播也不需要t的数据。

由此我们可以看出，整个反向传播的过程中都不需要变量t的数据。也就是说，为了传播梯度，计算图中需要变量t，但其数据可以立即删除。基于以上内容，我们按如下方式实现linear.simple函数。

dezero/functions.py

def linearsimple(x，W，b=None): t  $=$  matmul(x,W) if b is None: return t y  $=$  t  $^+$  b t.data  $=$  None #删除t的数据 returny

想象一下参数x和W为Variable实例或ndarray实例的情况。如果这些参数是ndarray实例，那么它们就会在matmul函数(准确来说是在Function类的__call__方法)中转换为Variable实例。另外，函数也允许省略偏置b，如果b=None，函数就只会计算矩阵的乘积并返回结果。

如果调用函数时提供了偏置参数，偏置就会被加到结果中。此时，作为中间结果的 $t$ 的数据在反向传播中就没有用了。因此，我们可以在计算完 $y = t + b$ 后使用 $t \cdot data = None$ 这行代码将其删除（引用计数变为0， $t$ 的数据被Python解释器删除）。

在神经网络中，大部分内存被作为中间计算结果的张量（ndarray实例）所占据。特别是在处理大的张量时，ndarray实例会非常大。因此，立即删除不要的narray实例是理想的做法。在这个例子中，我们手动(通过t.data = None)删除了不需要的ndarray实例，但其实这项操作也可以自动化。例如，Chainer中叫作Aggressive Buffer Release(参考文献[24])的机制就可以实现这一点。

以上就是改善内存使用的技巧。上面实现的linear-simple函数被添加到dezero/functions.py中。另外，继承自Function类的Linear类和linear函

数也在dezero/functions.py中实现。这些都是很简单的代码，有兴趣的读者可以自行查看。