20.1_Mul类的实现
20.1 Mul类的实现
假设有乘法运算 ,可得其导数为 和 。从这个结果可知,其反向传播的步骤如图20-1所示。
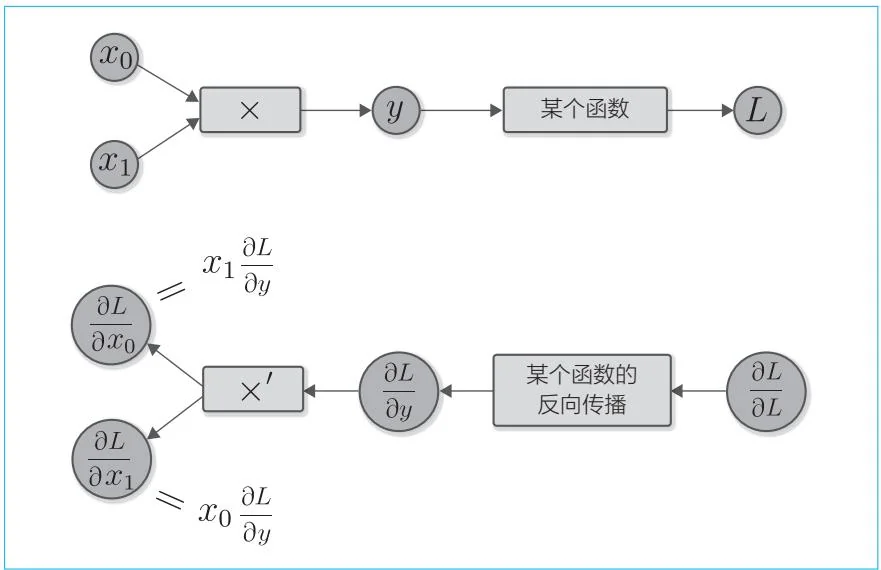
图20-1 乘法运算的正向传播(上图)和反向传播(下图)
如图20-1所示,反向传播中传播的是最终输出的 的导数,准确来说,是 对各变量的导数。这时, 对变量 和 的导数分别为 和 。

我们对输出标量的复合函数感兴趣,因此在图20-1中假设了复合函数最终会输出标量 。
下面实现Mul类。参照图20-1,Mul类可按如下方式实现
steps/step20.py
class Mul(Function): def forward(self, x0, x1): y = x0 * x1 return ydef backward(self, gy):
x0, x1 = self.inputs[0].data, selfinputs[1].data
return gy * x1, gy * x0接下来使用Mul类来实现一个Python函数mul。代码如下所示。
steps/step20.pydef mul(x0, x1):
return Mul()(x0, x1)现在可以使用mul函数进行乘法运算了。示例代码如下所示。
a = Variable(np.array(3.0))
b = Variable(np.array(2.0))
c = Variable(np.array(1.0))
y = add.mul(a, b), c)
y.backup()
print(y)
print(a.grad)
print(b.grad)运行结果
variable(7.0)
2.0
3.0上面的代码使用add函数和mul函数进行计算,还自动求出了y的导数。不过 这种写法让人有些不舒服。我们当然更喜欢 这种自然的写法。为了能使用运算符+和*进行计算,下面我们来扩展Variable。要想实现这个目标,需要重载运算符。

重载运算符后,在使用运算符 和 时,实际调用的就是用户设置的函数。在Python中,我们通过定义__add__和__mul__等特殊方法来调用用户指定的函数。