41.3 矩阵乘积的反向传播

下面介绍矩阵乘积的反向传播。矩阵乘积的反向传播有些复杂，这里先直接推导，之后进行补充说明以帮助大家直观理解。DeZero 的矩阵乘积计算在MatMul类和matmul函数中实现。matmul是matrix multiply的缩写。

下面以 $\pmb{y} = \pmb{x}\pmb{W}$ 为例介绍矩阵乘积的反向传播。在该计算中， $\pmb{x}$ 、 $\pmb{W}$ 和 $\pmb{y}$ 的形状分别为 $1\times D$ 、 $D\times H$ 和 $1\times H$ 。计算图如图41-3所示。

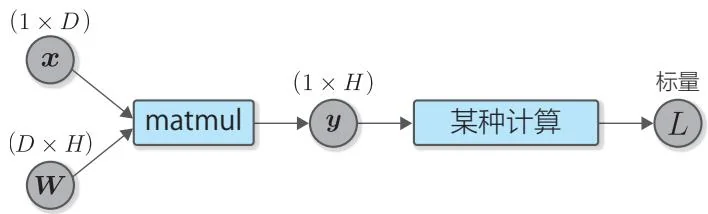
图41-3 矩阵乘积的正向传播（各变量上方标出了形状）

再次强调，我们处理的是最终会输出标量的计算。因此，假定计算最终输出的标量是 $L$ （通过反向传播求 $L$ 对每个变量的导数），此时， $L$ 对 $\pmb{x}$ 的第 $i$ 个元素的导数 $\frac{\partial L}{\partial x_i}$ 的式子如下所示。

式子41.2中的 $\frac{\partial L}{\partial x_i}$ 表示当 $x_{i}$ 发生(微小的)变化时 $L$ 的变化程度。当 $x_{i}$ 发生变化时，向量 $\pmb{y}$ 的所有元素也会发生改变。 $\pmb{y}$ 的每个元素的改变也会使 $L$ 最终发生变化。因此，从 $x_{i}$ 到 $L$ 有多条链式法则的路径，其总和为 $\frac{\partial L}{\partial x_i}$ 。

到式子41.2为止的推导过程还是很简单的。我们可以利用 $\frac{\partial y_j}{\partial x_i} = W_{ij}$ ①，将其代入式子41.2，推导出式子41.3。

从式子41.3可知， $\frac{\partial L}{\partial x_i}$ 可通过向量 $\frac{\partial L}{\partial y}$ 和 $\pmb{W}$ 的第 $i$ 行向量的内积求出由此我们可以推导出以下式子。

如式子41.4所示， $\frac{\partial L}{\partial x}$ 可通过矩阵的乘积一次性求出。此时矩阵(和向量)的形状的变化如图41-4所示。

1×D 1×H H×D

图41-4 检查矩阵乘积的形状

从图41-4可以看出，矩阵的形状没有问题。这也证实了式子41.4在计算矩阵时是成立的。我们也可以利用这个结论，也就是在矩阵乘法成立的基础上，推导出反向传播的式子(实现)①。在介绍该方法时，我们会再次思考 $\pmb{y} = \pmb{x}\pmb{W}$ 这个矩阵乘积的计算。不过这次我们假设 $\pmb{x}$ 的形状是 $N\times D$ 。换言之， $\pmb{x}$ 、 $\pmb{W}$ 和 $\pmb{y}$ 的形状分别为 $N\times D$ 、 $D\times H$ 和 $N\times H$ 。此时反向传播的计算图如图41-5所示。

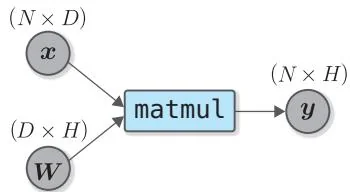
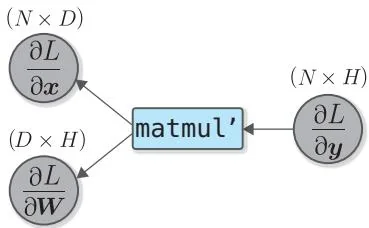
图41-5 矩阵乘积的正向传播（上图）和反向传播（下图）
图41-6 矩阵乘积的反向传播

下面来推导 $\frac{\partial L}{\partial x}$ 和 $\frac{\partial L}{\partial W}$ 。关注矩阵的形状，构建矩阵乘积的式子。推导出的式子如图41-6所示。

N×D）（N×H）（H×D）

D×H D×N (N×H)

与图41-4中的式子一样，图41-6中的式子也可以通过计算每个矩阵的元素并比较两边的结果推导出来。另外，我们也可以确认式子通过了矩阵乘积的形状检查。有了这个式子，就可以轻松实现执行矩阵乘积计算的DeZero函数了。代码如下所示。

dezero/functions.py

class MatMul Function): def forward(self, x, W): y = x.dot(W) return y def backward(self, gy): x, W = self.inputs gs = matmul(gy, W.T) gW = matmul(x.T, gy) return gx, gW   
def matmul(x, W): return MatMul() (x, W)

上面的代码根据图41-6中的式子实现了DeZero的反向传播函数。另外，在正向传播中，我们没有使用np.dot(x, W)，而是将计算实现为x.dot(W)。因此，它也可以作为ndarray实例的方法来使用。

在上面代码的反向传播中使用的matmul函数正是我们现在实现的函数。另外，用于转置的操作(W.T和x.T)会调用DeZero的transpose函数(该函数已在步骤38中实现)。

我们可以像下面这样使用DeZero的matmul函数来进行计算，也可以求出导数。

steps/step41.py

fromdezero import Variableimportdezero-functionsasF

$\begin{array}{rl} & {\mathrm{x} = \mathrm{Variable}(\mathrm{np}.random.\mathrm{randn}(2,3))}\\ & {\mathrm{W} = \mathrm{Variable}(\mathrm{np}.random.\mathrm{randn}(3,4))}\\ & {\mathrm{y} = \mathrm{F}.matmul(x,W)}\\ & {\mathrm{y}.backward()} \end{array}$    
print(x.grad.shape)   
print(W.grad.shape)

运行结果

(2,3)
(3,4)

上面的代码随机创建NumPy的多维数组，并用它们来进行计算。上述代码在运行时没有抛出任何错误。另外根据结果可知，x.grad.shape等于x.shape，w.grad.shape等于W.shape。这样就实现了DeZero版本的矩阵乘积。