0x52 背包

背包是线性DP中一类重要而特殊的模型，我们把它单独作为一节进行讲解。

0/1背包

0/1背包问题的模型如下：

给定 $N$ 个物品, 其中第 $i$ 个物品的体积为 $V_{i}$ , 价值为 $W_{i}$ 。有一容积为 $M$ 的背包, 要求选择一些物品放入背包, 使得物品总体积不超过 $M$ 的前提下, 物品的价值总和最大。

根据上一节线性DP的知识，读者应该很容易想到依次考虑每个物品是否放入背包，用“已经处理的物品数”作为DP的“阶段”，以“背包中已经放入的物品总体积”

作为附加维度。

$F[i,j]$ 表示从前 $i$ 个物品中选出了总体积为 $j$ 的物品放入背包，物品的最大价值和。

F [ i, j ] = \max \left\{ \begin{array}{l l} F [ i - 1, j ] & \text {不 选 第} i \text {个 物 品} \\ F [ i - 1, j - V _ {i} ] + W _ {i} & \text {选 第} i \text {个 物 品} \end{array} \right.

初值： $F[0,0] = 0$ ，其余均为负无穷，目标： $\max_{0\leq j\leq M}\{F[N][j]\}$

memset(f, 0xfc, sizeof(f)); // -INF
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
    for (int j = 0; j <= m; j++) {
        f[i][j] = f[i - 1][j];
    }
    for (int j = v[i]; j <= m; j++) {
        f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
    }
}

通过DP的状态转移方程，我们发现，每一阶段 $i$ 的状态只与上一阶段 $i - 1$ 的状态有关。在这种情况下，可以使用称为“滚动数组”的优化方法，降低空间开销。

int f[2][MAX_M+1];  
memset(f, 0xcf, sizeof(f)); // -INF  
f[0][0] = 0;  
for (int i = 1; i <= n; i++) {  
    for (int j = 0; j <= m; j++)  
        f[i & 1][j] = f[(i-1) & 1][j];  
    for (int j = v[i]; j <= m; j++)  
        f[i & 1][j] = max(f[i & 1][j], f[(i-1) & 1][j - v[i]] + w[i]);  
}  
int ans = 0;  
for (int j = 0; j <= m; j++)  
    ans = max(ans, f[n & 1][j]);

在上面的程序中，我们把阶段 $i$ 的状态存储在第一维下标为 $i\& 1$ 的二维数组中。当 $i$ 为奇数时， $i\& 1$ 等于 1；当 $i$ 为偶数时， $i\& 1$ 等于 0。因此，DP 的状态就相当于在 $F[0][]$ 和 $F[1][]$ 两个数组中交替转移，空间复杂度从 $O(NM)$ 降低为 $O(M)$ 。

进一步分析上面的代码，容易发现在每个阶段开始时，实际上执行了一次从 $F[i - 1]$

1[]到 $F[i][]$ 的拷贝操作。这提示我们可以进一步省略掉 $F$ 数组的第一维，只用一维数组，即当外层循环到第 $i$ 个物品时， $F[j]$ 表示背包中放入总体积为 $j$ 的物品的最大价值和。

int f[MAX_M+1];  
memset(f, 0xcf, sizeof(f)); // -INF  
f[0] = 0;  
for (int i = 1; i <= n; i++)  
    for (int j = m; j >= v[i]; j--)  
        f[j] = max(f[j], f[j - v[i]] + w[i]);  
int ans = 0;  
for (int j = 0; j <= m; j++)  
    ans = max(ans, f[j]);

请注意上面的代码片段中特别标注的部分——我们使用了倒序循环。循环到 $j$ 时：

$F$ 数组的后半部分 $F[j \sim M]$ 处于“第 $i$ 个阶段”，也就是已经考虑过放入第 $i$ 个物品的情况。
前半部分 $F[0 \sim j - 1]$ 处于“第 $i - 1$ 个阶段”，也就是还没有第 $i$ 个物品更新。

接下来 $j$ 不断减小，意味着我们总是用“第 $i - 1$ 个阶段”的状态向“第 $i$ 个阶段”的状态进行转移，符合线性DP的原则，进而保证了第 $i$ 个物品只会被放入背包一次，如下图所示。

然而，如果使用正序循环，假设 $F[j]$ 被 $F[j - V_i] + W_i$ 更新，接下来 $j$ 增大到 $j + V_i$ 时， $F[j + V_i]$ 又可能被 $F[j] + W_i$ 更新。此时，两个都处于“第 $i$ 个阶段”的状态之间发生了转移，违背了线性DP的原则，相当于第 $i$ 个物品被使用了两次，如下图所示。

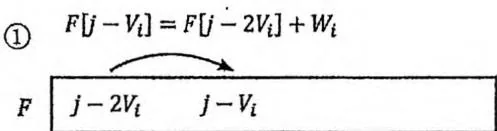
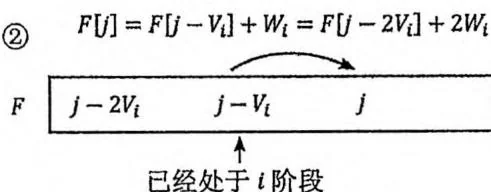
所以，在上面的代码中必须用倒序循环，才符合0/1背包问题中每个物品是唯一的、只能放入背包一次的要求。

【例题】数字组合 TYVJ1096

给定 $N$ 个正整数 $A_{1}, A_{2}, A_{3}, \dots, A_{N}$ ，从中选出若干个数，使它们的和是 $M$ ，求有多少种选择方案。 $1 \leq N \leq 100$ ， $1 \leq M \leq 10000$ ， $1 \leq A_{i} \leq 1000$ 。

这是一个典型的0/1背包模型， $N$ 个正整数就是 $N$ 个物品， $M$ 就是背包的容积。在外层循环到 $i$ 时（表示从前 $i$ 个数中选），设 $F[j]$ 表示“和为 $j$ ”有多少种方案。在具体实现中，只需要把上面代码中求max的函数改为求和即可。

int f[MAX_M+1];  
memset(f, 0, sizeof(f));  
f[0] = 1;  
for (int i = 1; i <= n; i++)  
    for (int j = m; j >= a[i]; j--)  
        f[j] += f[j - a[i]];  
cout << f[m] << endl;

$\spadesuit$ 完全背包

完全背包问题的模型如下：

给定 $N$ 种物品，其中第 $i$ 种物品的体积为 $V_{i}$ ，价值为 $W_{i}$ ，并且有无数个。有一容积为 $M$ 的背包，要求选择若干个物品放入背包，使得物品总体积不超过 $M$ 的前提下，物品的价值总和最大。

先来考虑使用传统的二维线性DP的做法。设 $F[i,j]$ 表示从前 $i$ 种物品中选出了总体积为 $j$ 的物品放入背包，物品的最大价值和。

F [ i, j ] = \max \left\{ \begin{array}{l l} F [ i - 1, j ] & \text {尚 未 选 过 第} i \text {种 物 品} \\ F [ i, j - V _ {i} ] + W _ {i} & \text {从 第} i \text {种 物 品 中 选 一 个} \end{array} \right.

初值： $F[0,0] = 0$ ，其余均为负无穷，目标： $\max_{0\leq j\leq M}\{F[N][j]\}$

与0/1背包一样，我们也可以省略 $F$ 数组的 $i$ 这一维。根据我们在0/1背包中对循环顺序的分析，当采用正序循环时，就对应着每种物品可以使用无限次，也对应着 $F[i,j] = F[i,j - V_i] + W_i$ 这个在两个均处于 $i$ 阶段的状态之间进行转移的方程。

int f[MAX_M+1];  
memset(f, 0xcf, sizeof(f)); // -INF  
f[0] = 0;  
for (int i = 1; i <= n; i++)

for (int j = v[i]; j <= m; j++)  
    f[j] = max(f[j], f[j - v[i]] + w[i]);  
int ans = 0;  
for (int j = 0; j <= m; j++)  
    ans = max(ans, f[j]);

【例题】自然数拆分Lunatic版 TYVJ1172

给定一个自然数 $N$ ，要求把 $N$ 拆分成若干个正整数相加的形式，参与加法运算的数可以重复。求拆分的方案数 mod 2147483648 的结果。 $1 \leq N \leq 4000$ 。

这是一个典型的完全背包模型， $1 \sim N$ 这 $N$ 个自然数构成 $N$ 种物品，每种物品都可以无限次使用，背包容积也是 $N$ 。与上一道例题类似，本题也是要求方案数，我们在完全背包程序模板的基础上，把求 $\max$ 的函数改为求和即可。

unsigned int f[MAX_M+1];  
memset(f, 0, sizeof(f));  
f[0] = 1;  
for (int i = 1; i <= n; i++)  
    for (int j = i; j <= n; j++)  
        f[j] = (f[j] + f[j - i]) % 2147483648u;  
cout << (f[n] > 0 ? f[n] - 1 : 2147483647) << endl;

【例题】Jury Compromise POJ1015

在一个遥远的国家，一名嫌犯是否有罪需要由陪审团来决定。陪审团是由法官从公民中挑选的。法官先随机挑选 $N$ 个人作为陪审团的候选人，然后再从这 $N$ 个人中按照下列方法选出 $M$ 人组成陪审团。

首先，参与诉讼的控方和辩方会给所有候选人打分，分值在0到20之间。第 $i$ 个人的得分分别记为 $a[i]$ 和 $b[i]$ 。为了公平起见，法官选出的 $M$ 个人必须满足：辩方总分 $D$ 和控方总分 $P$ 的差的绝对值 $|D - P|$ 最小。如果选择方法不唯一，那么再从中选择辩、控双方总分之和 $D + P$ 最大的方案。

求最终的陪审团获得的辩方总分 $D$ 、控方总值 $P$ ，以及陪审团人选的编号（方案）。 $1 \leq N \leq 200, 1 \leq M \leq 20$ 。

这是一道具有多个“体积维度”的0/1背包问题。把 $N$ 个候选人看作 $N$ 个物品，那么每个物品有如下三种“体积”：

“人数”，每个“候选人”的“人数”都是1，最终要填满容积为 $M$ 的背包。
“辩方得分”，即辩方给该候选人打的分数 $a[i]$ ，一个 $0 \sim 20$ 的整数。
“控方得分”，即控方给该候选人打的分数 $b[i]$ ，一个0~20的整数。

因此，我们依次考虑每个候选人是否选入评审团，当外层循环到阶段 $i$ 时，表示已经考虑了前 $i$ 个候选人的入选情况，此时用Boolean数组 $F[j,d,p]$ 表示已有 $j$ 人被选入评审团，当前辩方总分为 $d$ 、控方总分为 $p$ 的状态是否可行。

F [ j, d, p ] = F [ j, d, p ] \text {o r} F [ j - 1, d - a [ i ], p - b [ i ] ]

初值： $F[0,0,0] = \mathrm{true}$ ，其余均为false。

目标：找到一个状态 $F[M, d, p]$ ，满足 $F[M, d, p] = \text{true}$ ，并且 $|d - p|$ 尽量小， $|d - p|$ 相同时 $d + p$ 尽量大。

上述算法没有很好地利用背包“价值”这一维度，还有很大的优化空间。实际上，我们可以把每个候选人辩、控双方得分的差 $a[i] - b[i]$ 作为该物品的“体积”之一，把辩、控双方得分的和作为该物品的价值。

当外层循环到 $i$ 时，设 $F[j,k]$ 表示已经在前 $i$ 个候选人中选出了 $j$ 个，此时辩方总分与控方总分的差为 $k$ 时，辩方总分与控方总分的和的最大值。

F [ j, k ] = \max (F [ j, k ], F [ j - 1, k - (a [ i ] - b [ i ]) ] + a [ i ] + b [ i ])

初值： $F[0,0] = 0$ ，其余均为负无穷。

目标：找到一个状态 $F[M,k]$ ，满足 $|k|$ 尽量小，当 $|k|$ 相同时 $F[M,k]$ 尽量大。

在转移中，注意对 $j$ 这一维执行倒序循环，即可保证每个候选人只会被选一次，符合0/1背包的特征。

本题还要求输出评审团人选的具体方案。正如在上一节（0x51节）中提到的，我们采用记录转移路径的方法，即额外建立一个数组 $D$ ，其中 $D[j,k]$ 记录状态 $F[j,k]$ 的最大值是选了哪一名候选人而得到的。

在求出最优解后，我们沿着数组 $D$ 记录的转移路径，不断从状态 $F[j,k]$ 递归到 $F\bigl [j - 1,k - (a[D[j,k]] - b[D[j,k]]\bigr)\bigr ]$ ，直至到达 $F[0,0]$ 。递归过程中的所有 $D[j,k]$ 就构成了评审团的人选。

$\spadesuit$ 多重背包

多重背包问题的模型如下：

给定 $N$ 种物品，其中第 $i$ 种物品的体积为 $V_{i}$ ，价值为 $W_{i}$ ，并且有 $C_{i}$ 个。有一容积为 $M$ 的背包，要求选择若干个物品放入背包，使得物品总体积不超过 $M$ 的前提下，物品的价值总和最大。

直接拆分法

求解多重背包问题最直接的方法是把第 $i$ 种物品看作独立的 $C_i$ 个物品，转化为共有 $\sum_{i=1}^{N} C_i$ 个物品的 $0/1$ 背包问题进行计算，时间复杂度为 $O(M * \sum_{i=1}^{N} C_i)$ 。

unsigned int f[MAX_M+1];  
memset(f, 0xcf, sizeof(f)); // -INF  
f[0] = 0;  
for (int i = 1; i <= n; i++)  
    for (int j = 1; j <= c[i]; j++)  
        for (int k = m; k >= v[i]; k--)  
            f[k] = max(f[k], f[k - v[i]] + w[i]);  
int ans = 0;  
for (int i = 0; i <= m; i++)  
    ans = max(ans, f[i]);

上述算法把每种物品拆成了 $C_i$ 个，效率较低。

二进制拆分法

众所周知，从 $2^{0}, 2^{1}, 2^{2}, \dots, 2^{k-1}$ 这 $k$ 个 2 的整数次幂中选出若干个相加，可以表示出 $0 \sim 2^{k} - 1$ 之间的任何整数。进一步地，我们求出满足 $2^{0} + 2^{1} + \dots + 2^{p} \leq C_{i}$ 的最大的整数 $p$ ，设 $R_{i} = C_{i} - 2^{0} - 2^{1} - \dots - 2^{p}$ ，那么：

根据 $p$ 的最大性，有 $2^0 + 2^1 + \dots + 2^{p+1} > C_i$ ，可推出 $2^{p+1} > R_i$ ，因此 $2^0, 2^1, \dots, 2^p$ 选出若干个相加可以表示出 $0 \sim R_i$ 之间的任何整数。
从 $2^{0}, 2^{1}, \dots, 2^{p}$ 以及 $R_{i}$ 中选出若干个相加，可以表示出 $R_{i} \sim R_{i} + 2^{p+1} - 1$ 之间的任何整数，而根据 $R_{i}$ 的定义， $R_{i} + 2^{p+1} - 1 = C_{i}$ ，因此 $2^{0}, 2^{1}, \dots, 2^{p}, R_{i}$ 选出若干个相加可以表示出 $R_{i} \sim C_{i}$ 之间的任何整数。

综上所述，我们可以把数量为 $C_i$ 的第 $i$ 种物品拆成 $p + 2$ 个物品，它们的体积分别为：

2 ^ {0} * V _ {i}, 2 ^ {1} * V _ {i}, \dots , 2 ^ {p} * V _ {i}, R _ {i} * V _ {i}

这 $p + 2$ 个物品可以凑成 $0 \sim C_{i} * V_{i}$ 之间所有能被 $V_{i}$ 整除的数，并且不能凑成大于 $C_{i} * V_{i}$ 的数。这等价于原问题中体积为 $V_{i}$ 的物品可以使用 $0 \sim C_{i}$ 次。该方法仅把每种物品拆成了 $O(\log C_{i})$ 个，效率较高。

单调队列

使用单调队列优化的动态规划算法求解多重背包问题，时间复杂度可以进一步降低到 $O(NM)$ ，与0/1背包和完全背包中DP算法的效率相同，我们将在0x59节中进行讲解。

【例题】Coins POJ1742

给定 $N$ 种硬币，其中第 $i$ 种硬币的面值为 $A_{i}$ ，共有 $C_i$ 个。从中选出若干个硬

币，把面值相加，若结果为 $S$ ，则称“面值 $S$ 能被拼成”。求 $1 \sim M$ 之间能被拼成的面值有多少个。 $1 \leq N \leq 100, 1 \leq M \leq 10^{5}, 1 \leq A_{i} \leq 10^{5}, 1 \leq C_{i} \leq 1000$ 。

本题是一个多重背包模型，“硬币”为物品，“面值”为体积， $M$ 为背包总容积。这道题目中没有“物品价值”属性，不是一个最优化问题，而是一个可行性问题。按照我们方才介绍的DP算法，可以依次考虑每种硬币是否被用于拼成最终的面值（是否放入背包），以“已经考虑过的物品种数” $i$ 作为DP的“阶段”，在阶段 $i$ 时， $F[j]$ 表示前 $i$ 种硬币能否拼成面值 $j$ 。用“直接拆分法”朴素求解的代码片段如下：

bool f[100010];  
memset(f, 0, sizeof(f));  
f[0] = true;  
for (int i = 1; i <= n; i++)  
    for (int j = 1; j <= c[i]; j++)  
        for (int k = m; k >= a[i]; k--)  
            f[k] |= f[k - a[i]];  
int ans = 0;  
for (int i = 1; i <= m; i++)  
    ans += f[i];

上述算法的时间复杂度过高，不能通过本题的测试数据。当然，读者可以采用“二进制拆分法”或者“单调队列”进行优化。不过，本题仅关注“可行性”（面值能否拼成）而不是“最优性”，这是一个特殊之处。仔细分析动态规划的过程，我们可以发现，若前 $i$ 种硬币能够拼成面值 $j$ ，只有两类可能情况：

前 $i - 1$ 种硬币就能拼成面值 $j$ ，即在第 $i$ 阶段开始前，变量 $F[j]$ 已经为 true。
使用了第 $i$ 种硬币，即在第 $i$ 阶段的递推中，发现 $F[j - a[i]]$ 为 true，从而变量 $F[j]$ 变为 true。

于是我们可以考虑一种贪心策略：设 $used[j]$ 表示 $F[j]$ 在阶段 $i$ 时为 true 至少需要用多少枚第 $i$ 种硬币，并且尽量选择第一类情况。也就是说，在 $F[j - a[i]]$ 为 true 时，如果 $F[j]$ 已经为 true，则不执行 DP 的转移，并令 $used[j] = 0$ ，否则才执行 $F[j] = F[j]$ or $F[j - a[i]]$ 的转移，并令 $used[j] = used[j - a[i]] + 1$ 。

在“直接拆分法”程序的基础上，把核心部分作如下修改：

int used[100010];  
for (int i = 1; i <= n; i++) {  
    for (int j = 0; j <= m; j++) used[j] = 0;  
    for (int j = a[i]; j <= m; j++)

\begin{array}{l} i f \left(! f [ j ] \& \& f [ j - a [ i ] ] \& \& u s e d [ j - a [ i ] ] < c [ i ]\right) \\ f [ j ] = \text {t r u e}, \text {u s e d} [ j ] = \text {u s e d} [ j - a [ i ] ] + 1; \\ \end{array}

}

该程序使用了“完全背包”模型中 $j$ 的循环顺序，但通过 used 数组实现多重背包中“物品个数”的限制，同时根据贪心策略，仅当 $F[j]$ 为 false，不得不利用第 $i$ 种硬币时才执行转移，保证不会漏掉可行解。

分组背包

分组背包问题的模型如下：

给定 $N$ 组物品, 其中第 $i$ 组有 $C_i$ 个物品。第 $i$ 组的第 $j$ 个物品的体积为 $V_{ij}$ , 价值为 $W_{ij}$ 。有一容积为 $M$ 的背包, 要求选择若干个物品放入背包, 使得每组至多选择一个物品并且物品总体积不超过 $M$ 的前提下, 物品的价值总和最大。

仍然先考虑原始线性DP的做法。为了满足“每组至多选择一个物品”，很自然的想法就是利用“阶段”线性增长的特征，把“物品组数”作为DP的“阶段”，只要使用了一个第 $i$ 组的物品，就从第 $i$ 个阶段的状态转移到第 $i + 1$ 个阶段的状态。设 $F[i,j]$ 表示从前 $i$ 组中选出总体积为 $j$ 的物品放入背包，物品的最大价值和。

F[i,j] = \max \left\{ \begin{array}{c}F[i - 1,j]\\ \max_{1\leq k\leq C_{i}}F[i - 1,j - V_{ik}] + W_{ik} \end{array} \right.

不选第 $i$ 组的物品

选第 $i$ 组的某个物品 $k$

与前面几个背包模型一样，我们可以省略掉 $F$ 数组的第一维，用 $j$ 的倒序循环来控制“阶段 $i$ ”的状态只能从“阶段 $i - 1$ ”转移而来。

memset(f, 0xcf, sizeof(f));
f[0] = 0;
for (int i = 1; i <= n; i++) 
    for (int j = m; j >= 0; j--) 
    for (int k = 1; k <= c[i]; k++) 
        if (j >= v[i][k])
            f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

除了倒序循环 $j$ 之外，请读者格外留意，对于每一组内 $c[i]$ 个物品的循环 $k$ 应该放在 $j$ 的内层。从背包的角度看，这是因为每组内至多选择一个物品，若把 $k$ 置于 $j$ 的外层，就会类似于多重背包，每组物品在 $F$ 数组上的转移会产生累积，最终可以选择超过1个物品。从动态规划的角度， $i$ 是“阶段”， $i$ 与 $j$ 共同构成“状态”，而 $k$ 是“决策”——在第 $i$ 组内使用哪一个物品，这三者的顺序绝对不能混淆。

另外，分组背包是许多树形DP问题中状态转移的基本模型，读者在0x54节中将会进一步接触到它。

在本节中，我们介绍了0/1背包、完全背包、多重背包和分组背包。除了以传统的线性DP求解之外，我们还尽量缩减了空间复杂度，省去了“阶段”的存储，用适当的循环顺序控制状态在原有基础上直接转移和累积。请读者不要只把正确的循环顺序记住了事，务必要理解清楚其中的本质和内在联系。

0x52_背包