0x56 状态压缩 DP

在 $0 \times 51$ 节“线性DP”中，我们提到，动态规划的过程是随着“阶段”的增长，在每个状态维度上不断扩展的。在任意时刻，已经求出最优解的状态与尚未求出最优解的状态在各维度上的分界点组成了DP扩展的“轮廓”。对于某些问题，我们需要在动态规划的“状态”中记录一个集合，保存这个“轮廓”的详细信息，以便进行状态转移。若集合大小不超过 $N$ ，集合中每个元素都是小于 $K$ 的自然数，则我们可以把这个集合看作一个 $N$ 位 $K$ 进制数，以一个 $[0, K^{N} - 1]$ 之间的十进制整数的形式作为DP状态的一维。这种把集合转化为整数记录在DP状态中的一类算法，就被称为状态压缩的

动态规划算法。

0x01 节的例题“最短 Hamilton 路径”已经向读者展示了简单的状态压缩 DP 思想。在求解最短 Hamilton 路径时，整个状态空间可看作 $N$ 维，每维代表一个节点，只有 0（尚未访问）和 1（已访问）两个值。我们可以想象 DP 的“轮廓”以“访问过的节点数目”为阶段，从 $(0,0,\dots,0)$ 扩展到 $(1,1,\dots,1)$ 。为了记录当前状态在每个维度上的坐标是 0 还是 1，我们使用了一个 $N$ 位二进制数，即 $[0,2^{N} - 1]$ 之间的十进制整数存储节点的访问情况。另外，为了知道最后经过的节点是哪一个，我们把该节点编号作为附加信息，也保存在 DP 的状态中。因此，该状态压缩 DP 的状态数组就由大小分别为 $2^{N}$ 和 $N$ 的两个维度构成。在本节中，我们再探讨两道例题。

【例题】Mondriaan's Dream FOJ2411

求把 $N * M (1 \leq N, M \leq 11)$ 的棋盘分割成若干个 $1 * 2$ 的长方形，有多少种方案。例如当 $N = 2, M = 4$ 时，共有5种方案。当 $N = 2, M = 3$ 时，有3种方案。如下图所示：

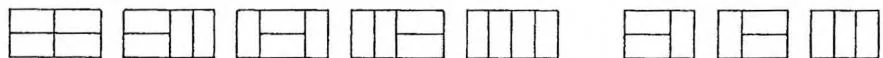
对于任意一种方案，考虑以某一行为界，把整个棋盘横着分成两半，如右图所示。在上半部分最后一行中：

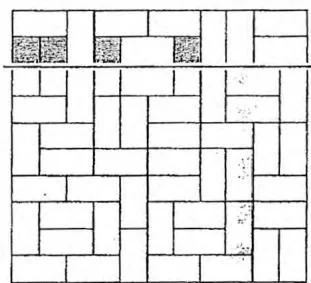
1. 每个灰色背景的部分都是一个竖着的 $1*2$ 长方形的一半，决定了下一行必须继续补全该长方形。

2. 其余部分对下半部分的分割方法没有影响。下一行既可以在连续两个位置安排一个横着的 $1*2$ 长方形，也可以让某个位置作为一个竖着的 $1*2$ 长方形的一半。

综上所述，我们可以把“行号”作为DP的“阶段”，把“上半部分”不断向下扩展，直至确定整个棋盘的分割方法。为了描述上半部分最后一行的详细形态，我们可以使用一个 $M$ 位二进制数，其中第 $k(0 \leq k < M)$ 位为1表示第 $k$ 列是一个竖着的 $1*2$ 长方形的上面一半，第 $k$ 位为0表示其他情况。

设 $F[i,j]$ 表示第 $i$ 行的形态为 $j$ 时，前 $i$ 行分割方案的总数。 $j$ 是用十进制整数记录的 $M$ 位二进制数。

第 $i - 1$ 行的形态 $k$ 能转移到第 $i$ 行的形态 $j$ ，当且仅当：

1. $j$ 和 $k$ 执行按位与运算的结果是0。

这保证了每个数字1的下方必须是数字0，代表继续补全竖着的 $1*2$ 长方形。

1. $j$ 和 $k$ 执行按位或运算的结果的二进制表示中，每一段连续的0都必须有偶数个。

这些0代表若干个横着的 $1 * 2$ 长方形，奇数个0无法分割成这种形态。

我们可以在DP前预处理出 $[0,2^M -1]$ 内所有满足“二进制表示下每一段连续的0都有偶数个”的整数，记录在集合 $S$ 中。

初值： $F[0,0] = 1$ ，其余均为0。

目标： $F[N,0]$

时间复杂度为 $O(2^{M}2^{M}N) = O(4^{M}N)$ 。

int n, m;  
long long f[12][1 << 11];  
bool in_s[1 << 11];  
int main() {  
    while (cin >> n >> m && n) {  
        for (int i = 0; i < 1 << m; i++) {  
            bool cnt = 0, hasOdd = 0;  
            for (int j = 0; j < m; j++)  
                if (i >> j & 1) hasOdd |= cnt, cnt = 0;  
                    else cnt ^= 1;  
            in_s[i] = hasOdd | cnt ? 0 : 1;  
        }  
        f[0][0] = 1;  
    for (int i = 1; i <= n; i++)  
        for (int j = 0; j < 1 << m; j++) {  
            f[i][j] = 0;  
            for (int k = 0; k < 1 << m; k++)  
                if ((j&k) == 0 && in_s[j | k])  
                    f[i][j] += f[i - 1][k];  
        }  
    cout << f[n][0] << endl;  
}

*【例题】炮兵阵地NOI2001/POJ1185

司令部的将军们打算在 $N * M$ 的网格地图上部署他们的炮兵部队。一个 $N * M$ 的地图由 $N$ 行 $M$ 列组成，地图的每一格可能是山地（用“H”表示），也可能是平原（用“P”表示），如右图所示。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队），一支炮兵部队在地图上的攻击范围如图中黑色区域所示。

如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其他白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少支我军的炮兵部队。 $N \leq 100, M \leq 10$ 。

本题与上一题类似，都是在矩形网格中放置图形的问题。上一题是求放满 $1*2$ 的长方形的方案数，本题则是求最多能放多少个“十字形状”，并且每个“十字”的中心都不被其他“十字”覆盖。因此，我们还是采用按“行号”为阶段的DP方法。

解法一

因为每个位置能否放置炮兵与它上面两行对应位置上是否放置炮兵有关，所以在向第 $i$ 行的状态转移时，需要知道第 $i - 1$ 行和第 $i - 2$ 行的状态。我们把每一行的状态看作一个 $M$ 位二进制数，用一个 $0 \sim 2^{M} - 1$ 之间的十进制整数存储，其中第 $p(0 \leq p < M)$ 位为1表示该行第 $p$ 列放置了炮兵，为0则表示没有放置炮兵。

我们在DP前预处理出集合 $S$ ，存储“相邻两个1的距离不小于3”的所有 $M$ 位二进制数，这些二进制数代表每一行中两个炮兵的距离不能小于3。

设 $\operatorname{count}(x)$ 表示 $M$ 位二进制数 $x$ 中1的个数。

设 $\operatorname{valid}(i, x)$ 表示 $M$ 位二进制数 $x$ 属于集合 $S$ ，并且 $x$ 中的每个1对应在地图第 $i$ 行中的位置都是平原。

设 $F[i,j,k]$ 表示第 $i$ 行压缩后的状态为 $j$ ，第 $i-1$ 行压缩后的状态为 $k$ 时，前 $i$ 行最多能摆放多少个炮兵。

初值： $F[0,0,0] = 0$ ，其余为负无穷。目标： $\max_{j|k = 0,\mathrm{valid}(N,j),\mathrm{valid}(N - 1,k)}\{F[N,j,k]\} .$

虽然 $M$ 位二进制数有 $2^{M}$ 个，但只有集合 $S$ 中的数才可能是合法状态。我们可以只对集合 $S$ 中的数进行循环，上述算法的时间复杂度为 $O(N|S|^2)$ 。事实上 $S$ 集合非常小。

解法二

我们把每个“十字”用如下数字表示：

这样每行的状态可压缩为一个 $M$ 位三进制数，用 $0 \sim 3^{M} - 1$ 之间的十进制整数存储。当第 $i - 1$ 行第 $j$ 列不为0时，第 $i$ 行第 $j$ 列不能放置炮兵。

设 $F[i,j]$ 表示第 $i$ 行压缩后的状态为三进制数 $j$ 时，前 $i$ 行最多能放多少个炮兵。像本题这种状态表示比较复杂、冗余的不合法状态较多的题目，我们不一定非要写出确切的状态转移方程。可以通过深度优先搜索（DFS），在保证合法的前提下，搜索第 $i + 1$ 行的每个位置填写什么数字，在到达搜索边界时（ $M$ 个位置都填完），就得到了一个状态 $k$ ，从而可以从 $F[i,j]$ 转移到 $F[i + 1,k]$ 。总而言之，整个动态规划算法使用三进制压缩的状态表示，以“行号”为阶段，在相邻两行之间使用 DFS 进行转移。

状态压缩DP的应用范围非常广泛，不局限于这两道“填充网格图形”的例题。就像本节开头提到的最短Hamilton路径问题一样，只要我们在动态规划时，需要把一个“集合”结构记录在状态中，就可以考虑采用压缩的方式转化为一个整数进行存储。当然，压缩后的这一维状态一般是指数级别的，因此状态压缩DP解决的许多问题通常还是NPC问题，但相比直接搜索而言，效率会有不小的提升。