0x63 树的直径与最近公共祖先

树的直径

给定一棵树，树中每条边都有一个权值，树中两点之间的距离定义为连接两点的路径上的边权之和。树中最远的两个节点之间的距离被称为树的直径，连接这两点的路径被称为树的最长链。后者通常也可称为直径，即直径既是一个数值概念，也可代指一条路径。

树的直径一般有两种求法，时间复杂度都是 $O(N)$ 。我们假设树以 $N$ 个点 $N - 1$

条边的无向图的形式给出，并存储在邻接表中。

树形DP求树的直径

不妨设1号节点为根，“ $N$ 个点 $N - 1$ 条边的无向图”就可以看作“有根树”。

设 $D[x]$ 表示从节点 $x$ 出发走向以 $x$ 为根的子树，能够到达的最远节点的距离。设 $x$ 的子节点为 $y_{1}, y_{2}, \dots, y_{t}$ ， $\operatorname{edge}(x, y)$ 表示边权，显然有：

接下来，我们可以考虑对每个节点 $x$ 求出“经过节点 $x$ 的最长链的长度” $F[x]$ ，整棵树的直径就是 $\max_{1 \leq x \leq n} \{F[x]\}$ 。

那么如何求出 $F[x]$ 呢？对于 $x$ 的任意两个节点 $y_{i}$ 和 $y_{j}$ ，“经过节点 $x$ 的最长链的长度”可以通过四个部分构成：从 $y_{i}$ 到 $y_{i}$ 子树中的最远距离，边 $(x, y_{i})$ ，边 $(x, y_{j})$ ，从 $y_{j}$ 到 $y_{j}$ 子树中的最远距离。不妨设 $j < i$ ，因此：

我们没有必要使用两层循环来枚举 $i, j$ 。请读者思考计算 $D[x]$ 的过程。在子节点的循环将要枚举到 $i$ 时， $D[x]$ 恰好就保存了从节点 $x$ 出发走向“以 $y_j (j < i)$ 为根的子树”，能够到达的最远节点的距离，这个距离就是 $\max_{1 \leq j < i} \{D[y_j] + \text{edge}(x, y_j)\}$ 。所以，此时我们先用 $D[x] + D[y_i] + \text{edge}(x, y_i)$ 更新 $F[x]$ ，再用 $D[y_i] + \text{edge}(x, y_i)$ 更新 $D[x]$ 即可。

void dp(int x) {
    v[x] = 1;
    for (int i = head[x]; i; i = Next[i]) {
        int y = ver[i];
        if (v[y]) continue;
        dp(y);
        ans = max(ans, d[x] + d[y] + edge[i]);
        d[x] = max(d[x], d[y] + edge[i]);
    }
}

两次BFS求树的直径

通过两次BFS或者两次DFS也可以求出树的直径，并且更容易计算出直径上的具体节点。详细地说，这种做法包括两步：

1. 从任意一个节点出发，通过 BFS 或 DFS 对树进行一次遍历，求出与出发点距离最远的节点，记为 $p$ 。

2. 从节点 $p$ 出发, 通过 BFS 或 DFS 再进行一次遍历, 求出与 $p$ 距离最远的节点, 记为 $q$ 。

从 $p$ 到 $q$ 的路径就是树的一条直径。这是因为 $p$ 一定是直径的一端，否则总能找到一条更长的链，与直径的定义矛盾。请读者尝试详细证明这个结论，此处就不再赘述。既然 $p$ 是直径的一端，那么与 $p$ 距离最远的 $q$ 当然就是直径的另一端了。

在第2步的遍历过程中，可以记录下来每个点第一次被访问时的前驱节点。最后从 $q$ 递归回到 $p$ ，即可得到直径的具体方案。

树的直径可以作为很多树上问题的突破口。接下来我们给出两道例题。除此之外，读者还将在0x6B节的练习中解决树的直径的必须边等问题。

【例题】巡逻 GPIO2010/BZOJ1912

在一个地区中有 $n$ 个村庄，编号为 $1,2,\dots ,n$ 。有 $n - 1$ 条道路连接着这些村庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其他任一个村庄。每条道路的长度均为1个单位。

为保证该地区的安全，巡警车每天要到所有的道路上巡逻。警察局设在编号为1的村庄里，每天巡警车总是从警察局出发，最终又回到警察局。

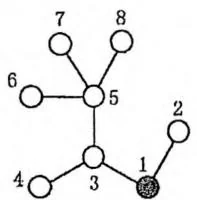
下图表示一个有8个村庄的地区，其中村庄用圆表示（其中村庄1用黑色的圆表示），道路是连接这些圆的线段。为了遍历所有的道路，巡警车需要走的距离为14个单位，每条道路都需要经过两次。

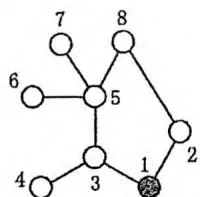
为了减少总的巡逻距离，该地区准备在这些村庄之间建立 $K$ 条新的道路，每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束，见下面的图例(c)。一条新道路甚至可以是一个环，即其两端连接到同一个村庄。因为资金有限， $K$ 只能是1或2。同时，为了不浪费资金，每天巡警车必须经过新建的道路正好一次。下图给出了一些建立新道路的例子。

(a)

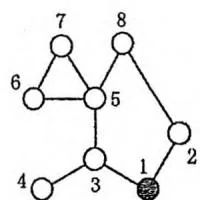
(b)

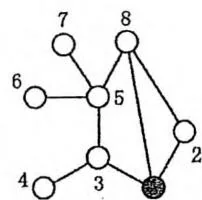
(c)

在(a)中，新建了一条道路，总的距离是11。在(b)中，新建了两条道路，总的巡逻距离是10。在(c)中，新建了两条道路，但因为巡警车要经过每条新道路正好一次，总的距离变为了15。

试编写一个程序, 读取村庄间道路的信息和需要新建的道路数, 计算出最佳的新建

道路的方案，使得总的巡逻距离最小，并输出这个最小的巡逻距离。

数据范围： $3\leq n\leq 10^{5}$ ， $1\leq K\leq 2$

不建立新的道路时，从1号节点出发，把整棵树上的每条边遍历至少一次，再回到1号节点，会恰好经过每条边两次，路线总长度为 $2(n - 1)$ ，如下图最左边的部分所示。根据树的深度优先遍历思想，很容易证明这个结论，因为每条边必然被递归一次、回溯一次。

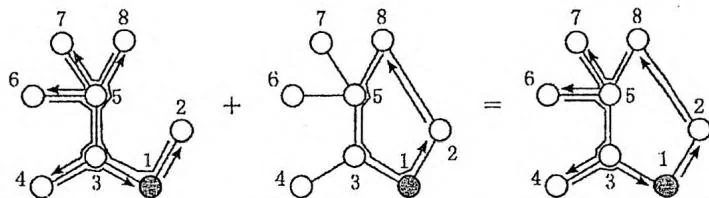
建立1条新道路之后，因为新道路必须经过恰好一次（0次、2次都不可以），所以在沿着新道路 $(x,y)$ 巡逻之后，要返回 $x$ ，就必须沿着树上从 $y$ 到 $x$ 的路径巡逻一遍，最终形成一个环。与不建立新道路的情况相结合，相当于树上 $x$ 与 $y$ 之间的路径就只需经过一次了，如上图所示。

因此，当 $K = 1$ 时，我们找到树的最长链，在两个端点之间加一条新道路，就能让总的巡逻距离最小。若树的直径为 $L$ ，答案就是 $2(n - 1) - L + 1$ 。

建立第2条新道路 $(u, v)$ 之后，又会形成一个环。若两条新道路形成的环不重叠，则树上 $u, v$ 之间的路径只需经过一次，答案继续减小。否则，在两个环重叠的情况下，如果我们还按照刚才的方法把第2个环与建立1条新道路的情况相结合，两个环重叠的部分就不会被巡逻到，如下图所示。因为题目要求每条道路必须被巡逻，我们不得不让巡逻车在适当的时候重新巡逻这些边，并且返回。最终的结果是两个环重叠的部分由“只需经过一次”变回了“需要经过两次”。

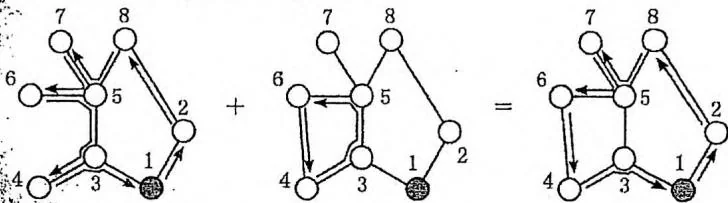
综上所述，我们得到了如下算法：

1. 在最初的树上求直径, 设直径为 $L_{1}$ 。然后把直径上的边权取反 (从 1 改为 -1)。

2. 在最长链边权取反之后的树上再次求直径，设直径为 $L_{2}$ 。

答案就是 $2(n - 1) - (L_1 - 1) - (L_2 - 1) = 2n - L_1 - L_2$ 。如果 $L_2$ 这条直径包含 $L_1$ 取反的部分，就相当于两个环重叠。减掉 $(L_1 - 1)$ 后，重叠的部分变成了“只需经过一次”，减掉 $(L_2 - 1)$ 后，相当于把重叠的部分加回来，变回“需要经过两次”，与我们之前的讨论相符。时间复杂度为 $O(n)$ 。

【例题】树网的核 NOIP2007/BZOJ1999

设 $T = (V, E, W)$ 是一个无环且连通的无向图（也称为无根树），每条边带有正整数的权值，我们称 $T$ 为树网（Tree Network），其中 $V, E$ 分别表示节点与边的集合， $W$ 表示各边长度的集合，并设 $T$ 有 $n$ 个节点。

路径：树网中任何两个节点 $a, b$ 都存在唯一的一条简单路径，用 $d(a, b)$ 表示以 $a, b$ 为端点的路径的长度，它是该路径上各边长度之和。我们称 $d(a, b)$ 为 $a, b$ 两节点之间的距离。

一点 $v$ 到一条路径 $P$ 的距离为该点与 $P$ 上的最近的节点的距离：

树网的直径：树网中最长的路径称为树网的直径。对于给定的树网 $T$ ，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个节点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。

偏心距 $ECC(F)$ ：树网 $T$ 中距路径 $F$ 最远的节点到路径 $F$ 的距离，即：

任务：对于给定的树网 $T = (V, E, W)$ 和非负整数 $s$ ，求一个路径 $F$ ，它是某直径上的一段路径（该路径两端均为树网中的节点），其长度不超过 $s$ （可以等于 $s$ ），使偏心距 $ECC(F)$ 最小。我们称这个路径为树网 $T = (V, E, W)$ 的核（Core）。必要时， $F$ 可以退化为某个节点。一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。

NOIP 原题数据范围: $5 \leq n \leq 300$ , $0 \leq s \leq 1000$ 。BZOJ 加强版: $n \leq 5 * 10^{5}$ 。

题目已经告诉我们，树的直径不唯一，但所有直径必定相交，并且各直径的中点汇聚于同一处。进一步可以得到一个推论：在任意一条直径上求出的最小偏心距都相等。请读者思考这两条结论为什么成立。

解法一：枚举， $O(n^{3})$

我们很容易想到一个朴素解法。首先，通过两次BFS求出任意一条直径（最长链）。然后，在直径上枚举距离不超过 $s$ 的两个点 $p$ 和 $q$ ， $p, q$ 之间的路径就作为“树网的核”，同时，我们把核上的每个节点标记为“已访问”。接下来，从核上的每个节点出发，执行深度优先遍历（不经过有“已访问”标记的节点），求出核以外的每个节点到核的距离，取最大值就得到了核的偏心距。在所有枚举的核中取最小值，就是最小偏心距，即本题答案。整个算法的时间复杂度为 $O(n^{3})$ 。

解法二：枚举+贪心， $O(n^{2})$

根据贪心策略，在树网的核的一端 $p$ 固定后，另一端 $q$ 在距离不超过 $s$ 的前提下，显然越远越好。因此我们只需在直径上枚举 $p$ ，然后直接确定 $q$ 的位置，再按照

上述算法执行深度优先遍历，时间复杂度可以降低到 $O(n^{2})$ 。

解法三：二分答案， $O(n\log SUM)$

为了通过加强版数据，我们还需进一步优化。容易发现，本题的答案具有单调性，可以二分答案，把问题转化为“验证是否存在一个核，其偏心距不超过二分的值mid”。

设直径的两个端点为 $u$ 和 $v$ 。在直径上找到与 $u$ 的距离不超过 mid 的前提下，距离 $u$ 最远的节点，作为节点 $p$ 。类似地，在直径上找到与 $v$ 的距离不超过 mid 的前提下，距离 $v$ 最远的节点，作为节点 $q$ 。

根据直径的最长性，任何从 $u, p$ 之间分叉离开直径的子树，其最远点与 $p$ 的距离都不会比 $u$ 更远。所以 $p, q$ 就是在满足直径两侧的那部分节点偏心距不超过 mid 的前提下，尽量靠近树网中心的节点。

接下来，我们还需检查 $p, q$ 的距离是否不超过 $s$ ，同时用深度优先遍历检查把 $p, q$ 之间的路径作为树网的核时，离核最远的点的距离是否也不超过 $s$ 。如果两个条件都满足，就判定验证成功， $p, q$ 之间的路径就是偏心距不超过 mid 的一个合法的核。

该二分算法的时间复杂度为 $O(n \log SUM)$ ，其中 $SUM$ 表示树网所有边的长度之和。

解法四：分析性质，直接扫描， $O(n)$

我们还可以不用二分法，而是用单调队列，把时间复杂度进一步优化到 $O(n)$ 。

设直径上的节点为 $u_{1}, u_{2}, \dots, u_{t}$ 。与前面几个解法类似，先把这 $t$ 个节点标记为“已访问”，然后通过深度优先遍历，求出 $d[u_{i}]$ ，表示从 $u_{i}$ 出发，不经过直径上的其他节点，能够到达的最远点的距离。

以 $u_{i}, u_{j} (i \leq j)$ 为端点的树网的核的偏心距就是：

此时用单调队列维护 $\max_{i\leq k\leq j}\{d[u_k]\}$ ，已经能做到 $O(n)$ 了。但这还不够完美，根据解法三中提到的直径的最长性，上式实际上可简化为：

$\max_{1 \leq k \leq t} \{d[u_k]\}$ 对于 $u_i, u_j$ 来说是一个定值。所以我们只需枚举直径上的每个点 $u_i$ ，同时用一个指针，在距离不超过 $s$ 的前提下，每次沿着直径向后移动，得到 $u_j$ ，然后更新答案即可。对于每个 $i$ ，指针 $j$ 的位置是单调递增的，故时间复杂度为 $O(n)$ 。

经过不断的思考、分析，最终我们没有采用任何高级的算法，仅靠遍历、扫描，就非常简洁、高效地解决了本题。虽然很多问题的时间复杂度是有下界的，但从某种程度上说，算法的设计、优化是永无止境的。读者不应被已有的思维束缚，或只满足于得到

AC，而是应该尽可能地挖掘、总结一个模型的相关性质，探究其本质。截至作者完稿，使用搜索引擎都会发现一个有趣的现象，网络上的多数题解均采用了floyd、单调队列等不必要的解法，提出不同思路者甚少，由此可见，很多算法学习者抄题解而欠思考的现象极其严重，这是每位读者应该避免的行为。

$\spadesuit$ 最近公共祖先(LCA)

给定一棵有根树，若节点 $z$ 既是节点 $x$ 的祖先，也是节点 $y$ 的祖先，则称 $z$ 是 $x, y$ 的公共祖先。在 $x, y$ 的所有公共祖先中，深度最大的一个称为 $x, y$ 的最近公共祖先，记为 $\operatorname{LCA}(x, y)$ 。

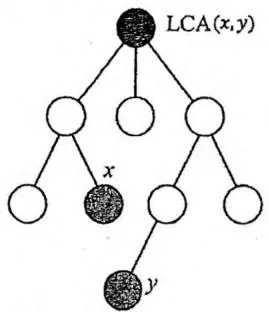
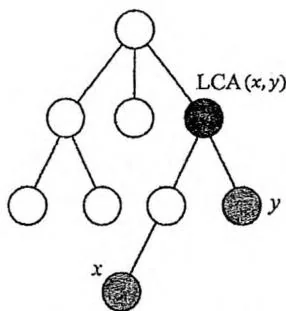
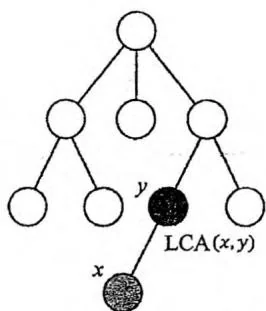
$\operatorname{LCA}(x, y)$ 是 $x$ 到根的路径与 $y$ 到根的路径的交会点。它也是 $x$ 与 $y$ 之间的路径上深度最小的节点。求最近公共祖先的方法通常有三种：

向上标记法

从 $x$ 向上走到根节点，并标记所有经过的节点。

从 $y$ 向上走到根节点，当第一次遇到已标记的节点时，就找到了 $\operatorname{LCA}(x, y)$ 。

对于每个询问，向上标记法的时间复杂度最坏为 $O(n)$ 。

树上倍增法

树上倍增法是一个很重要的算法。除了求LCA之外，它在很多问题中都有广泛应用。设 $F[x, k]$ 表示 $x$ 的 $2^k$ 辈祖先，即从 $x$ 向根节点走 $2^k$ 步到达的节点。特别地，若该节点不存在，则令 $F[x, k] = 0$ 。 $F[x, 0]$ 就是 $x$ 的父节点。除此之外， $\forall k \in [1, \log n]$ ， $F[x, k] = F[F[x, k - 1], k - 1]$ 。

这类似于一个动态规划的过程，“阶段”就是节点的深度。因此，我们可以对树进行广度优先遍历，按照层次顺序，在节点入队之前，计算它在 $F$ 数组中相应的值。

以上部分是预处理，时间复杂度为 $O(n \log n)$ ，之后可以多次对不同的 $x, y$ 计算 LCA，每次询问的时间复杂度为 $O(\log n)$ 。

基于 $F$ 数组计算 $\operatorname{LCA}(x, y)$ 分为以下几步：

1. 设 $d[x]$ 表示 $x$ 的深度。不妨设 $d[x] \geq d[y]$ （否则可交换 $x, y$ ）。

2. 用二进制拆分思想，把 $x$ 向上调整到与 $y$ 同一深度。

具体来说，就是依次尝试从 $x$ 向上走 $k = 2^{\log n}, \dots, 2^{1}, 2^{0}$ 步，检查到达的节点是否比 $y$ 深。在每次检查中，若是，则令 $x = F[x, k]$ 。

1. 若此时 $x = y$ ，说明已经找到了LCA，LCA就等于 $y$ 。

这就是上面的图中的第三种情况。

1. 用二进制拆分思想，把 $x, y$ 同时向上调整，并保持深度一致且二者不相会。

具体来说，就是依次尝试把 $x, y$ 同时向上走 $k = 2^{\log n}, \dots, 2^{1}, 2^{0}$ 步，在每次尝试中，若 $F[x, k] \neq F[y, k]$ （即仍未相会），则令 $x = F[x, k], y = F[y, k]$ 。

1. 此时 $x, y$ 必定只差一步就相会了，它们的父节点 $F[x, 0]$ 就是 LCA。

请读者画图理解，并参阅下面的程序。程序以模板题HDOJ2586“How far away?”为例，多次查询树上两点之间的距离，时间复杂度 $O((n + m)\log n)$ 。

const int SIZE = 50010;  
int f[SIZE][20], d[SIZE], dist[SIZE];  
int ver[2 * SIZE], Next[2 * SIZE], edge[2 * SIZE], head[SIZE];  
int T, n, m, tot, t;  
queue<int> q;

void add(int x, int y, int z) {
    ver[++tot] = y; edge[tot] = z; Next[tot] = head[x]; head[x] = tot;
}

void bfs(){//预处理q.push(1);d[1] = 1;while (q.size()){int  $\mathbf{x} =$  q.front();q.pop();for(inti  $=$  head[x];i；i  $=$  Next[i]) {inty  $=$  ver[i];if(d[y])continue;d[y]  $= d[x] + 1$  dist[y]  $=$  dist[x]  $^+$  edge[i];f[y][0]  $= x$  for(intj  $= 1$  ;j<=t;j++)f[y][j]  $=$  f[f[y][j-1]][j-1];q.push(y);

}   
}   
int lca(int x, int y) { // 回答一个询问 if  $(\mathrm{d}[x] > \mathrm{d}[y])$  swap(x, y); for (int i = t; i >= 0; i--) if  $(\mathrm{d}[f[y][i]] >= d[x])$  y = f[y][i]; if (x == y) return x; for (int i = t; i >= 0; i--) if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i]; return f[x][0];   
}   
int main() { cin >> T; while (T--){ cin >> n >> m; t = (int)(log(n) / log(2)) + 1; //清空 for (int i = 1; i <= n; i++) head[i] = d[i] = 0; tot = 0; //读入一棵树 for (int i = 1; i < n; i++) { int x, y, z; scanf("%d%d%d", &x, &y, &z); add(x, y, z), add(y, x, z); } bfs(); //回答问题 for (int i = 1; i <= m; i++) { int x, y; scanf("%d%d", &x, &y); printf("%d\n", dist[x] + dist[y] - 2 * dist[lca(x, y)]; }

LCA的Tarjan算法

Tarjan 算法本质上是使用并查集对“向上标记法”的优化。它是一个离线算法，需要把 $m$ 个询问一次性读入，统一计算，最后统一输出。时间复杂度为 $O(n + m)$ 。

在深度优先遍历的任意时刻，树中节点分为三类：

1. 已经访问完毕并且回溯的节点。在这些节点上标记一个整数 2。

2. 已经开始递归，但尚未回溯的节点。这些节点就是当前正在访问的节点 $x$ 以及 $x$ 的祖先。在这些节点上标记一个整数 1。
   3.尚未访问的节点。这些节点没有标记。

对于正在访问的节点 $x$ ，它到根节点的路径已经标记为1。若 $y$ 是已经访问完毕并且回溯的节点，则 $\operatorname{LCA}(x, y)$ 就是从 $y$ 向上走到根，第一个遇到的标记为1的节点。

可以利用并查集进行优化，当一个节点获得整数2的标记时，把它所在的集合合并到它的父节点所在的集合中（合并时它的父节点标记一定为1，且单独构成一个集合）。

这相当于每个完成回溯的节点都有一个指针指向它的父节点，只需查询 $y$ 所在集合的代表元素（并查集的 get 操作），就等价于从 $y$ 向上一直走到一个开始递归但尚未回溯的节点（具有标记 1），即 $\mathrm{LCA}(x, y)$ 。

在 $x$ 回溯之前，标记情况与合并情况如下图所示。黑色表示标记为1，灰色表示标记为2，白色表示没有标记，箭头表示执行了合并操作。

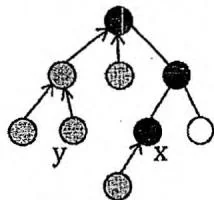
此时扫描与 $x$ 相关的所有询问，若询问当中的另一个点 $y$ 的标记为 2，就知道了该询问的回答应该是 $y$ 在并查集中的代表元素（并查集中 get(y) 函数的结果）。

下面的参考程序以模板题HDOJ2586“How far away?”为例，多次查询树上两点之间的距离，时间复杂度为 $O(n + m)$ 。

const int SIZE = 50010;  
int ver[2 * SIZE], Next[2 * SIZE], edge[2 * SIZE], head[SIZE];  
int fa[SIZE], d[SIZE], v[SIZE], lca[SIZE], ans[SIZE];  
vector<int> query[SIZE], query_id[SIZE];  
int T, n, m, tot, t;  
void add(int x, int y, int z) {  
    ver[++tot] = y; edge[tot] = z; Next[tot] = head[x]; head[x] = tot;  
}

void add_query(int x, int y, int id) {
    query[x].push_back(y), query_id[x].push_back(id);
    query[y].push_back(x), query_id[y].push_back(id);
}  
int get(int x) {
    if (x == fa[x]) return x;
    return fa[x] = get(fa[x]);
}  
void tarjan(int x) {
    v[x] = 1;
    for (int i = head[x]; i; i = Next[i]) {
        int y = ver[i];
        if (v[y]) continue;
        d[y] = d[x] + edge[i];
        tarjan(y);
        fa[y] = x;
    }
    for (int i = 0; i < query[x].size(); i++) {
        int y = query[x][i], id = query_id[x][i];
        if (v[y] == 2) {
            int lca = get(y);
            ans[id] = min( ans[id], d[x] + d[y] - 2 * d[lca]);
        }
    }
    v[x] = 2;
}  
int main() {
    cin >> T;
    while (T--){
        cin >> n >> m;
        for (int i = 1; i <= n; i++) {
            head[i] = 0; fa[i] = i, v[i] = 0;
            query[i].clear(), query_id[i].clear();
        }
        tot = 0;

for (int i = 1; i < n; i++) { int x, y, z; scanf("%d%d%d", &x, &y, &z); add(x, y, z), add(y, x, z); } for (int i = 1; i <= m; i++) { int x, y; scanf("%d%d", &x, &y); if (x == y) ans[i] = 0; else { add_query(x, y, i); ans[i] = 1 << 30; } } tarjan(1); for (int i = 1; i <= m; i++) printf("%d\n", ans[i]); }

【例题】闇の連鎖 FOJ3417

传说中的“闇の連鎖”被人们称为Dark。Dark是人类内心的黑暗的产物，古今中外的勇者们都试图打倒它。经过研究，你发现Dark呈现无向图的结构，图中有N个节点和两类边，一类边被称为主要边，而另一类被称为附加边。Dark有N-1条主要边，并且Dark的任意两个节点之间都存在一条只由主要边构成的路径。另外，Dark还有M条附加边。

你的任务是把 Dark 斩为不连通的两部分。一开始 Dark 的附加边都处于无敌状态，你只能选择一条主要边切断。一旦你切断了一条主要边，Dark 就会进入防御模式，主要边会变为无敌的，而附加边可以被切断。但是你的能力只能再切断 Dark 的一条附加边。现在你想要知道，一共有多少种方案可以击败 Dark。注意，就算你第一步切断主要边之后就已经把 Dark 斩为两截，你也需要切断一条附加边才算击败了 Dark。

$N \leq 10^{5}$ , $M \leq 2 * 10^{5}$ 。数据保证答案不超过 $2^{31} - 1$ 。

根据题意，“主要边”构成一棵树，“附加边”则是“非树边”。把一条附加边 $(x, y)$ 添加到主要边构成的树中，会与树上 $x, y$ 之间的路径一起形成一个环。如果第一步选择切断 $x, y$ 之间路径上的某条边，那么第二步就必须切断附加边 $(x, y)$ ，才能令 Dark 被斩为不连通的两部分。

因此，我们称每条附加边 $(x, y)$ 都把树上 $x, y$ 之间的路径上的每条边“覆盖了一次”。我们只需统计出每条“主要边”被覆盖了多少次。若第一步把被覆盖0次的主要边切断，则第二步可任意切断一条附加边。若第一步把被覆盖1次的主要边切断，则第二步方法唯一。若第一步把被覆盖2次及2次以上的主要边切断，则第二步无论如何操作都不能击败Dark。这样我们就得到了击败Dark的方案数。

综上所述，下面我们要解决的问题模型是：给定一张无向图和一棵生成树，求每条“树边”被“非树边”覆盖了多少次。下图左侧的例子中标记了覆盖次数，虚线为“非树边”。

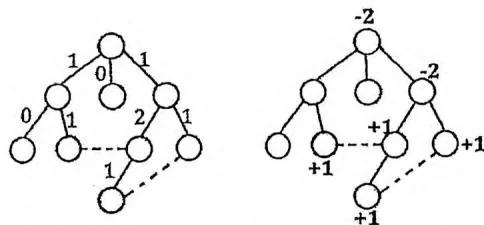
解决此问题有一个经典做法，我们称之为“树上差分算法”。树上差分算法与差分序列的思想类似，在之前的一些问题中，我们曾多次把“区间”的增减转化为“左端点加1，右端点减1”，请读者回顾。对应在树上，我们给每个节点一个初始为0的权值，然后对每条非树边 $(x,y)$ ，令节点 $x$ 的权值加1，节点 $y$ 的权值加1，节点 $\operatorname{LCA}(x,y)$ 的权值减2，如上图右侧的例子所示。最后对这棵生成树进行一次深度优先遍历，求出 $F[x]$ 表示以 $x$ 为根的子树中各节点的权值之和。 $F[x]$ 就是 $x$ 与它的父节点之间的“树边”被覆盖的次数。时间复杂度 $O(N + M)$ 。

【例题】异象石 ContestRunter#56-C

Adera是Microsoft应用商店中的一款解谜游戏。

异象石是进入Adera中异时空的引导物，在Adera的异时空中有一张地图。这张地图上有 $N$ 个点，有 $N - 1$ 条双向边把它们连通起来。起初地图上没有任何异象石，在接下来的 $M$ 个时刻中 $(1 \leq N, M \leq 10^{5})$ ，每个时刻会发生以下三种类型的事件之一：

1. 地图的某个点上出现了异象石（已经出现的不会再次出现）。

2. 地图某个点上的异象石被摧毁（不会摧毁没有异象石的点）。

3. 向玩家询问使所有异象石所在的点连通的边集的总长度最小是多少。

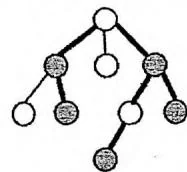
请你作为玩家回答这些问题。右侧是一个例子，灰色节点表示出现了异象石，加粗的边表示被选为连通异象石的边集。

根据题意，这张地图显然构成一棵树。先对这棵树进行深度优先遍历，求出每个点

的时间戳（0x21节已经介绍了时间戳的概念）。

仔细思考可以发现，如果我们按照时间戳从小到大的顺序，把出现异象石的节点排成一圈（首尾相接），并且累加相邻两个节点之间的路径长度，最后得到的结果恰好是所求答案的两倍。如下图所示，黑色节点表示按照时间戳顺序依次选定的两个节点，加粗的边表示二者之间的路径。五幅图合起来，恰好把上图中加粗的边集覆盖了两次。

因此，我们可以用一个数据结构（例如 C++ STLset），按照时间戳递增的顺序，维护出现异象石的节点序列，并用一个变量 ans 记录序列中相邻两个节点之间的路径长度之和（序列首尾也看作是相邻的）。

设 $\operatorname{path}(x, y)$ 表示树上 $x, y$ 之间的路径长度，设 $d[x]$ 表示 $x$ 到根节点的路径长度。我们有 $\operatorname{path}(x, y) = d[x] + d[y] - 2 * d[\mathrm{LCA}(x, y)]$ 。 $d$ 数组可通过一次深度优先遍历全部求出， $\operatorname{path}(x, y)$ 可用树上倍增法求出 LCA 计算。

若一个节点出现了异象石，就依据时间戳，把它插入到上述节点序列中适当的位置。设插入的节点为 $x$ ，它在序列中前后分别是节点 $l$ 和 $r$ ，我们就令 ans 减去 path $(l, r)$ ，加上 path $(l, x) + \text{path}(x, r)$ 。若一个节点的异象石被摧毁，则类似地更新异象石节点序列以及变量 ans 的值。对于每个询问，直接输出 ans 即可。

整个算法的时间复杂度为 $O\big((N + M)\log N\big)$

【例题】次小生成树 BZOJ1977

给定一张 $N$ 个点 $M$ 条边的无向图，求无向图的严格次小生成树。设最小生成树的边权之和为 $sum$ ，严格次小生成树就是指边权之和大于 $sum$ 的生成树中最小的一个。

数据范围： $N\leq 10^{5}$ ， $M\leq 3*10^{5}$ 。

先求出任意一棵最小生成树，设边权之和为sum。我们称在这棵最小生成树中的 $N - 1$ 条边为“树边”，其他 $M - N + 1$ 条边为“非树边”。

把一条非树边 $(x, y, z)$ 添加到最小生成树中，会与树上 $x, y$ 之间的路径一起形成一个环。设树上 $x, y$ 之间的路径上的最大边权为 $val_{1}$ ，严格次大边权为 $val_{2} (val_{1} > val_{2})$ 。

若 $z > val_{1}$ ，则把 $val_{1}$ 对应的那条边替换成 $(x, y, z)$ 这条边，就得到了严格次小生成树的一个候选答案，边权之和为 $sum - val_{1} + z$ 。

若 $z = \text{val}_1$ ，则把 $\text{val}_2$ 对应的那条边替换成 $(x, y, z)$ 这条边，就得到了严格次小生成树的一个候选答案，边权之和为 $\text{sum} - \text{val}_2 + z$ 。

枚举每条非树边，添加到最小生成树中，计算出上述所有“候选答案”。在候选答案中取最小值就得到了整张无向图的严格次小生成树。因此，我们要解决的主要问题是：如何快速求出一条路径上的最大边权与严格次大边权。

可以用树上倍增算法来进行预处理。设 $F[x, k]$ 表示 $x$ 的 $2^k$ 辈祖先， $G[x, k, 0]$ 与 $G[x, k, 1]$ 分别表示从 $x$ 到 $F[x, k]$ 的路径上的最大边权和严格次大边权（最大边权不等于次大边权）。于是 $\forall k \in [1, \log N]$ 有：

当 $k = 0$ 时，有初值：

接下来，我们考虑每条非树边 $(x, y, z)$ 。采用倍增计算 $\operatorname{LCA}(x, y)$ 的框架， $x, y$ 每向上移动一段路径，就把该段路径对应的最大边权、严格次大边权按照与求 $G$ 数组类似的方法合并到答案中，最后即可得到树上 $x, y$ 之间的路径上的最大边权、严格次大边权。

整个算法的时间复杂度为 $O(M \log N)$ 。

【例题】疫情控制 NOIP2012/CODEVS1218

H 国有 $n$ 个城市，这 $n$ 个城市用 $n - 1$ 条双向道路相互连通构成一棵树，1 号城市是首都，也是树中的根节点。

H国的首都爆发了一种危害性极高的传染病。当局为了控制疫情，不让疫情扩散到边境城市（叶子节点所表示的城市），决定动用军队在一些城市建立检查点，使得从首都到边境城市的每一条路径上都至少有一个检查点，边境城市也可以建立检查点。但要注意的是，首都是不能建立检查点的。

现在，在H国的一些城市中已经驻扎有军队，且一个城市可以驻扎多个军队。军队总数为 $m$ 支。一支军队可以在有道路连接的城市间移动，并在除首都以外的任意一个城市建立检查点，且只能在一个城市建立检查点。一支军队经过一条道路从一个城市移动到另一个城市所需要的时间等于道路的长度（单位：小时）。

请问：最少需要多少个小时才能控制疫情？注意：不同的军队可以同时移动。

数据范围： $2\leq m\leq n\leq 5*10^{4}$ 。

为了叙述方便，若从首都（根节点）到边境城市（叶子节点） $x$ 的途中经过了军队 $i$ ，我们就称军队 $i$ 管辖了节点 $x$ 。本题要求我们保证每个叶子节点都有军队管辖。显然，在不移动到根节点的前提下，军队所在的节点深度越浅，能管辖的叶子节点越多。

本题的答案也满足单调性——若 $ans$ 个小时能控制疫情，则对于任意 $k \geq ans$ ， $k$ 个小时当然也能控制疫情。因此可考虑二分答案，把问题转化为：判定二分的值 mid 小时内能否控制疫情。

军队可分为两类。第一类是在mid小时内无法到达根节点的军队。对于这些军队，就让他们尽量往根节点走，mid小时内能走到哪里，最终就驻扎在哪里即可。

记根节点的子节点集合为 $\mathsf{son}(\mathsf{root})$ 。处理完第一类军队后，对每个节点 $s \in \mathsf{son}(\mathsf{root})$ ，统计以 $s$ 为根的子树中是否还有叶子节点尚未被管辖。设 $H$ 是 $\mathsf{son}(\mathsf{root})$ 中还有叶子节点尚未被管辖的节点组成的集合。

第二类是在mid小时内能够到达根节点的军队。我们先让这些军队移动到根节点的子节点上（差一步到根节点），用三元组 $(i,s,rest)$ 代表。其中 $i$ 表示军队编号， $s$ 表示军队来自根节点的哪一个子节点，rest表示军队 $i$ 移动到 $s$ 之后还剩余多少时间。这些军队有两种使用方法：仍然驻扎在 $s$ ，或者跨过根节点去管辖其他的子树。

引理：

若存在一支军队 $(i, s, \text{rest})$ , 满足 $s \in H$ 并且军队 $i$ 在 rest 时间内无法从 $s$ 移动到根再返回 $s$ , 则在最优解中, $s$ 一定被自己子树内部的一支军队驻扎, 不可能由其他子树的军队跨过根节点过来驻扎。

证明：

因为 $s \in H$ ，所以需要安排一支军队驻扎在 $s$ 。假设 $s$ 由来自另一个子树 $s'$ 的军队 $i'$ 跨过根节点来驻扎，从 $s'$ 到 $s$ 所需时间为 $\mathrm{dist}(root, s') + \mathrm{dist}(root, s)$ 。

因为存在一支军队 $(i, s, \text{rest})$ 无法从 $s$ 移动到根再返回 $s$ , 所以这支军队要么闲置, 要么只能跨过根节点驻扎在比 $s$ 离根更近的节点 $s''$ 。故对任意的 $s''$ , 根据 $\text{dist}(\text{root}, s) > \text{dist}(\text{root}, s'')$ 可知, $i'$ 一定也有足够的时间去管辖子树 $s''$ 。

综上所述，让 $i$ 驻扎在自己的子树 $s$ ，把 $i'$ 留作他用，未来的可能性更多，答案不会更差。由贪心的决策包容性可知引理成立。

证毕。

根据这条引理，对于 $\forall s\in H$ ，若 $s$ 上有军队，并且 $s$ 上rest值最小的军队不足以移动到根再返回 $s$ ，我们就让 $s$ 上这支rest值最小的军队驻扎在 $s$ ，管辖以 $s$ 为根的子树。同时，从集合 $H$ 中删除 $s$ 。

现在，仍未确定驻扎地点的军队都可以使用第二类方法——跨过根节点去管辖其他子树。集合 $H$ 中剩余的节点就是需要被驻扎的位置。我们把集合 $H$ 中的节点按照

到根的距离从小到大排序，把剩余的军队按照“rest减去 $s$ 到根的距离”从小到大排序，执行一个贪心扫描算法，让剩余时间短的军队优先驻扎到离根近的节点，让剩余时间长的军队优先驻扎到离根远的节点，判断最后能否把 $H$ 中的节点全部管辖，就知道二分的值是否可行了。整个算法的时间复杂度为 $O\big((n + m)\log n\log SUM\big)$ ，其中SUM表示所有边的长度之和。