0x68 二分图的匹配

如果一张无向图的 $N$ 个节点 $(N\geq 2)$ 可以分成 $A,B$ 两个非空集合，其中 $A\cap B = \emptyset$ ，并且在同一集合内的点之间都没有边相连，那么称这张无向图为一张二分图。 $A,B$ 分别称为二分图的左部和右部。

$\Leftrightarrow$ 二分图判定

定理

一张无向图是二分图，当且仅当图中不存在奇环（长度为奇数的环）。

证明略。

根据该定理，我们可以用染色法进行二分图的判定。大致思想为：尝试用黑白两种颜色标记图中的节点，当一个节点被标记后，它的所有相邻节点应该被标记与它相反的颜色。若标记过程中产生冲突，则说明图中存在奇环。二分图染色一般基于深度优先遍历实现，其流程如下，时间复杂度为 $O(N + M)$

void dfs(int x, int color)  
赋值  $\mathrm{v}[\mathrm{x}] \leftarrow \mathrm{color}$   
对于与  $\mathbf{x}$  相连的每条无向边(x,y)  
if  $\mathrm{v}[\mathrm{y}] = 0$  then  
dfs(y, 3-color)  
else if  $\mathrm{v}[\mathrm{y}] \neq \mathrm{color}$   
判定无向图不是二分图，算法结束  
在主函数中  
for i < 1 to N  
if  $\mathrm{v}[i] = 0$  then dfs(i, 1)  
判定无向图是二分图

【例题】关押罪犯 NOIP2010/CODEVS1069

S城现有两座监狱,一共关押着 $N$ 名罪犯,编号分别为 $1 \sim N$ 。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久,如果客观条件具备则随时可能爆发冲突。

我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为 $c$ 的罪犯被关押在同一监狱，他们之间会发生摩擦，并造成影响力为 $c$ 的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到S城Z市长那里。公务繁忙的Z市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了 $N$ 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。

那么，应如何分配罪犯，才能使Z市长看到的那个冲突事件的影响力最小？这个最小值是多少？罪犯数量 $N \leq 2 * 10^{4}$ ，仇恨关系的数量 $M \leq 10^{5}$ 。

在0x47节“数据结构进阶”的练习中，我们要求读者用并查集解决了本题。此处我们换用二分图判定的方法再次求解。

考虑这样一个判定问题：是否存在一种分配罪犯的方案，使Z市长看到的那个冲突事件的影响力不超过mid。显然，当mid较小时可行的方案，对于更大的mid仍然可行。换言之，本题的答案具有单调性，可以通过二分法，把求最值的问题转化为判定问题。

二分答案，设当前二分的值为 $mid$ 。此时，任意两个仇恨程度大于 $mid$ 的罪犯都必须被安排在不同的监狱。我们把罪犯作为节点，在仇恨程度大于 $mid$ 的两个罪犯之间连边，得到一张无向图。这张无向图的节点需要被分成两个集合（两个监狱），并且每个集合内部没有边（同一个监狱内没有仇恨程度大于 $mid$ 的罪犯）。所以，我们用染色法判定该无向图是否为二分图即可。若是二分图，则令二分上界 $r = mid$ ，否则令下界 $l = mid + 1$ 。

$\diamond$ 二分图最大匹配

“任意两条边都没有公共端点”的边的集合被称为图的一组匹配。在二分图中，包含边数最多的一组匹配被称为二分图的最大匹配。

对于任意一组匹配 $S$ （ $S$ 是一个边集），属于 $S$ 的边被称为“匹配边”，不属于 $S$ 的边被称为“非匹配边”。匹配边的端点被称为“匹配点”，其他节点被称为“非匹配点”。如果在二分图中存在一条连接两个非匹配点的路径 path，使得非匹配边与匹配边在 path 上交替出现，那么称 path 是匹配 $S$ 的增广路，也称交错路。

增广路显然具有以下性质：

1.长度len是奇数。

1. 路径上第 $1,3,5,\dots ,len$ 条边是非匹配边，第 $2,4,6,\dots ,len - 1$ 条边是匹配边。

正因为以上性质，如果我们把路径上所有边的状态取反，原来的匹配边变成非匹配的，原来的非匹配边变成匹配的，那么得到的新的边集 $S^{\prime}$ 仍然是一组匹配，并且匹配边数增加了1。进一步可以得到推论：

二分图的一组匹配 $S$ 是最大匹配，当且仅当图中不存在 $S$ 的增广路。

匈牙利算法（增广路算法）

匈牙利算法，又称增广路算法，用于计算二分图最大匹配。它的主要过程为：

1. 设 $S = \varnothing$ ，即所有边都是非匹配边。

2.寻找增广路path，把路径上所有边的匹配状态取反，得到一个更大的匹配 $S^{\prime}$

1. 重复第2步，直至图中不存在增广路。

该算法的关键在于如何找到一条增广路。匈牙利算法依次尝试给每一个左部节点 $x$ 寻找一个匹配的右部节点 $y$ 。右部点 $y$ 能与左部点 $x$ 匹配，需要满足以下两个条件之一：

1. $y$ 本身就是非匹配点。

此时无向边 $(x, y)$ 本身就是非匹配边，自己构成一条长度为 1 的增广路。

1. $y$ 已经与左部点 $x^{\prime}$ 匹配，但从 $x^{\prime}$ 出发能找到另一个右部点 $y^\prime$ 与之匹配。

此时路径 $x\sim y\sim x^{\prime}\sim y^{\prime}$ 为一条增广路。

在实际的程序实现中，我们采用深度优先搜索的框架，递归地从 $x$ 出发寻找增广路。若找到，则在深搜回溯时，正好把路径上的匹配状态取反。另外，可以用全局 bool 数组标记节点的访问情况，避免重复搜索。

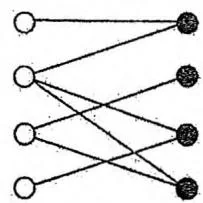
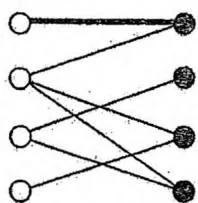
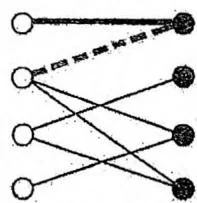
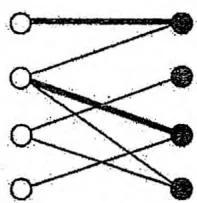
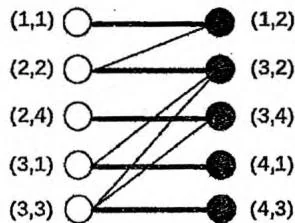
左部点3找到匹配

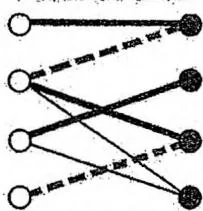
左4尝试匹配右3，递归左2尝试匹配右1, 失败

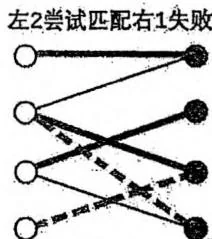
左2继续尝试右4 成功找到增广路

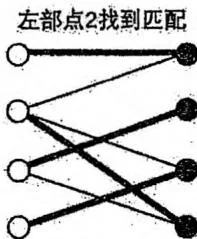
回溯时把增广路取反左部点4也得以匹配

匈牙利算法的正确性基于贪心策略，它的一个重要特点是：当一个节点成为匹配点后，至多因为找到增广路而更换匹配对象，但是绝不会再变回非匹配点。

对于每个左部节点，寻找增广路最多遍历整张二分图一次。因此，该算法的时间复杂度为 $O(NM)$ 。

bool dfs(int x) {  
    for (int i = head[x], y; i; i = next[i])  
        if (!visit[y = ver[i]]) {  
            visit[y] = 1;  
            if (!match[y] || dfs(match[y])) {  
                match[y] = x; return true;  
            }  
        }  
    return false;  
}  
for (int i = 1; i <= n; i++) { // 在 main 函数中  
                memset.visit, 0, sizeof.visit);  
                if (dfs(i)) ans++;  
}

【例题】棋盘覆盖 TYVJ1035

给定一个 $N$ 行 $M$ 列的棋盘，已知某些格子禁止放置。求最多能往棋盘上放多少块的长度为2、宽度为1的骨牌，骨牌的边界与格线重合（骨牌占用两个格子），并且任意两张骨牌都不重叠。 $N, M \leq 50$ 。

在0x56节“状态压缩DP”的例题“Mondriaan'sDream”中，我们解决了用 $1*2$ 的长方形铺满 $N*M$ 网格的方案数问题。与之不同的是，本题的棋盘有禁止放置的格子，并且只需求出能放置的 $1*2$ 骨牌的最大数量。当 $N,M$ 较小时，依然可以用状态压缩DP解决，更高效的方法则是构建出二分图匹配的模型。

二分图匹配的模型有两个要素：

1.节点能分成独立的两个集合，每个集合内部有0条边。
2. 每个节点只能与 1 条匹配边相连。

我们把它简称为“0要素”和“1要素”。在把实际问题抽象成二分图匹配时，我们就要寻找题目中具有这种“0”和“1”性质的对象，从而发现模型构建的突破口。

在本题中，任意两张骨牌都不重叠，也就是每个格子只能被1张骨牌覆盖。而骨牌的大小为 $1*2$ ，覆盖2个相邻的格子。这恰好与“1要素”相对应。于是，我们可以

把棋盘上没有被禁止的格子作为节点，把骨牌作为无向边（两个相邻的格子对应的节点之间连边）。

如果把棋盘黑白染色（行号加列号为偶数的格子染成白色，行号加列号为奇数的格子染成黑色），那么两个相同颜色的格子不可能被同一骨牌覆盖，也就是同色格子之间没有边相连。这恰好与“0要素”对应。于是，刚才建立的无向图是一张二分图，可把白色格子作为左部节点，黑色格子作为右部节点。

要让骨牌不重叠的情况下尽量多放，就是求上述二分图的最大匹配。使用匈牙利算法，时间复杂度为 $O(N^{2}M^{2})$

【例题】車的放置

给定一个 $N$ 行 $M$ 列的棋盘，已知某些格子禁止放置。问棋盘上最多能放多少个不能互相攻击的车。车放在格子里，攻击范围与中国象棋的“车”一致。 $N, M \leq 200$ 。

“1要素”：每行、每列只能放1个車（不然就能互相攻击到）。某个格子 $(i,j)$ 如果放了車，就等于占用了第 $i$ 行与第 $j$ 列放車的“名额”。

因此，我们可以把行、列看作节点，一共 $N + M$ 个节点。如果格子 $(i,j)$ 没有被禁止，就在第 $i$ 行对应的节点与第 $j$ 行对应的节点之间连无向边。

“0要素”：每个車显然不能既在第 $i_1$ 行又在第 $i_2$ 行，所以两个“行”对应的节点之间没有边。对于“列”也同理。

因此，刚才构建的无向图是二分图，我们可以把 $N$ 个“行节点”作为左部， $M$ 个“列节点”作为右部。

要在不能互相攻击的前提下放置的車最多，就是求上述二分图的最大匹配。时间复杂度为 $O\big((N + M)*N*M\big)$ 。

完备匹配

给定一张二分图，其左部、右部节点数相同，均为 $N$ 个节点。如果该二分图的最大匹配包含 $N$ 条匹配边，则称该二分图具有完备匹配。

多重匹配

给定一张包含 $N$ 个左部节点、 $M$ 个右部节点的二分图。从中选出尽量多的边，

使第 $i(1 \leq i \leq N)$ 个左部节点至多与 $kl_{i}$ 条选出的边相连，第 $j(1 \leq j \leq M)$ 个右部节点至多与 $kr_{j}$ 条选出的边相连。该问题被称为二分图的多重匹配。

当 $kl_{i} = kr_{j} = 1$ 时，上述问题就简化为二分图最大匹配。因此，多重匹配是一个广义的“匹配”问题，每个节点可以与不止一条“匹配”边相连，但不能超过一个给定的限制。

多重匹配一般有四种解决方案：

1. 拆点。把第 $i$ 个左部节点拆成 $kl_{i}$ 个不同的左部节点，第 $j$ 个右部节点拆成 $kr_{j}$ 个右部节点。对于原图中的每条边 $(i,j)$ ，在 $i$ 拆成的所有节点与 $j$ 拆成的所有节点之间连边。然后求解二分图最大匹配。

2. 如果所有的 $k l_{i} = 1$ ，或者所有的 $k r_{j} = 1$ ，即只有一侧是“多重”匹配，不妨设左部是“多重”的，那么可以直接在匈牙利算法中让每个左部节点执行 $k l_{i}$ 次 dfs。

3. 在第2种方案中，当然也可以交换左右两部，设“右部”是多重的，修改匈牙利算法的实现，让右部节点可以匹配 $kr_{j}$ 次，超过匹配次数后，就要依次尝试递归当前匹配的 $kr_{j}$ 个左部节点，看能否找到增广路。
   4.网络流。这是最一般也是最高效的解决方法，我们将在0x6A节讲解。

【例题】导弹防御塔 TYVJ1935

Freda 的城堡遭受了 $M$ 个入侵者的攻击! Freda 控制着 $N$ 座导弹防御塔, 每座塔都有足够数量的导弹, 但是每次只能发射一枚。在发射导弹时, 导弹需要 $T_{1}$ 秒才能从防御塔中射出, 而在发射导弹后, 发射这枚导弹的防御塔需要 $T_{2}$ 分钟来冷却。

所有导弹都有相同的匀速飞行速度 $V$ , 并且会沿着距离最短的路径去打击目标。计算防御塔到目标的距离 Distance 时, 你只需要计算水平距离, 而忽略导弹飞行的高度。导弹在空中飞行的时间就是 (Distance/V) 分钟, 导弹到达目标后可以立即将它击毁。

现在，给出 $N$ 座导弹防御塔的坐标， $M$ 个入侵者的坐标， $T_{1}, T_{2}$ 和 $V$ 。因为 Freda 的小伙伴 Rainbow 就要来拜访城堡了，你需要求出至少多少分钟才能击退所有的入侵者。

数据范围： $1\leq N,M\leq 50,T_{1},T_{2},V < = 2000$ ，坐标绝对值不超过10000。

时间较短时如果能击退所有入侵者，那么对于更长的时间，显然也能击退入侵者，因此本题的答案具有单调性。二分答案，设当前二分的值为 $mid$ ，问题转化为判定“能否在 $mid$ 秒之内击退所有入侵者”。

“1要素”：每个入侵者被攻击1次后就会被击退。每座塔虽然可以发射很多枚导弹，但是每枚导弹只能攻击1个入侵者。

已知发射预热时间 $T_{1}$ 、冷却时间 $T_{2}$ ，我们容易计算出每座塔在mid分钟内至多能发射出多少枚导弹，记为 $P$ 。容易发现，本题是一个多重匹配问题，可以把入侵者作

为二分图左部节点，每座防御塔拆成 $P$ 个导弹，作为二分图右部节点。最终共有 $M$ 个左部节点、 $N * P$ 个右部节点。

注意，因为防御塔、入侵者的坐标各不相同，所以从塔飞到入侵者的时间也可能不同。我们在连边时，还需要检查导弹是否有足够的时间飞到入侵者。因此，一座塔的 $P$ 个导弹是不等价的，这个多重匹配问题必须用拆点法解决。如果在 mid 时间内，第 $i(1 \leq i \leq M)$ 个入侵者能被第 $j(1 \leq j \leq N)$ 座塔的第 $k(1 \leq k \leq P)$ 个导弹击中，那么就在第 $i$ 个左部点和第 $(j - 1)*P + k$ 个右部点之间连一条无向边。

用匈牙利算法计算二分图的最大匹配。若每个左部点都能找到匹配，则说明mid分钟内能击退所有入侵者，可令二分上界 $r = mid$ ，否则令下界 $l = mid + 1$ 。

$\Leftrightarrow$ 二分图带权匹配

给定一张二分图，二分图的每条边都带有一个权值。求出该二分图的一组最大匹配，使得匹配边的权值总和最大。这个问题称为二分图的带权最大匹配，也称二分图最优匹配。注意，二分图带权最大匹配的前提是匹配数最大，然后再最大化匹配边的权值总和。

二分图带权最大匹配有两种解法：费用流和KM算法。本节先来介绍KM算法，费用流将在0x6A节进行讲解。KM算法程序实现简单，在稠密图上的效率一般高于费用流。不过，KM算法有很大的局限性，只能在满足“带权最大匹配一定是完备匹配”的图中正确求解。所以一般情况下，本书鼓励读者采用费用流来计算二分图带权最大匹配。

在接下来的讨论中，我们设二分图左、右两部的节点数均为 $N$ 。

交错树

在匈牙利算法中，如果从某个左部节点出发寻找匹配失败，那么在DFS的过程中，所有访问过的节点，以及为了访问这些节点而经过的边，共同构成一棵树。

这棵树的根是一个左部节点，所有叶子节点也都是左部节点（因为最终匹配失败了），并且树上第 $1,3,5,\dots$ 层的边都是非匹配边，第 $2,4,6,\dots$ 层的边都是匹配边。因此，这棵树被称为交错树。

顶标

全称“顶点标记值”。在二分图中，给第 $i(1 \leq i \leq N)$ 个左部节点一个整数值 $A_{i}$ ，给第 $j(1 \leq j \leq N)$ 个右部节点一个整数值 $B_{j}$ 。同时，必须满足 $\forall i, j, A_{i} + B_{j} \geq w(i, j)$ ，其中 $w(i, j)$ 表示第 $i$ 个左部点与第 $j$ 个右部点之间的边权（没有边时设为负无穷）。这些整数值 $A_{i}, B_{j}$ 称为节点的顶标。

相等子图

二分图中所有节点和满足 $A_{i} + B_{j} = w(i,j)$ 的边构成的子图，称为二分图的相等子图。

定理

若相等子图中存在完备匹配，则这个完备匹配就是二分图的带权最大匹配。

证明：

在相等子图中，完备匹配的边权之和等于 $\sum_{i=1}^{N}(A_i + B_i)$ ，即所有顶标之和。

因为顶标满足 $\forall i,j,A_{i} + B_{j}\geq w(i,j)$ ，所以在整个二分图中，任何一组匹配的边权之和都不可能大于所有顶标的和。

证毕。

KM 算法的基本思想就是，先在满足 $\forall i, j, A_i + B_j \geq w(i, j)$ 的前提下，给每个节点随意赋值一个顶标，然后采取适当策略不断扩大相等子图的规模，直至相等子图存在完备匹配。例如，我们可以赋值 $A_i = \max_{1 \leq j \leq N} \{w(i, j)\}$ ， $B_j = 0$ 。

对于一个相等子图，我们用匈牙利算法求它的最大匹配。若最大匹配不完备，则说明一定有一个左部节点匹配失败。该节点匹配失败的那次DFS形成了一棵交错树，记为 $T$ 。

考虑匈牙利算法的流程，容易发现以下两条结论：

1. 除了根节点以外， $T$ 中其他的左部点都是从右部点沿着匹配边访问到的，即在程序中调用了 dfs(match[y])，其中 $y$ 是一个右部节点。

2. $T$ 中所有的右部点都是从左部点沿着非匹配边访问到的。

在寻找到增广路以前，我们不会改变已有的匹配，所以一个右部点沿着匹配边能访问到的左部点是固定的。为了让匹配数增加，我们只能从第2条结论入手，考虑“怎样能让左部点沿着非匹配边访问到更多的右部点”。

假如我们把交错树 $T$ 中的所有左部节点顶标 $A_{i}(i \in T)$ 减小一个整数值 $\Delta$ , 把 $T$ 中的所有右部节点顶标 $B_{j}(j \in T)$ 增大一个整数值 $\Delta$ , 节点的访问情况会有哪些变化? 我们分两方面进行讨论:

1. 右部点 $j$ 沿着匹配边，递归访问 $i = \text{match}[j]$ 的情形。

对于一条匹配边，显然要么 $i, j \in T$ （被访问到了），要么 $i, j \notin T$ （没被访问到）。故 $A_i + B_j$ 不变，匹配边仍然属于相等子图。

1. 左部点 $i$ 沿着非匹配边，访问右部点 $j$ ，尝试与之匹配的情形。

因为左部点的访问是被动的（被右部点沿着匹配边递归），所以只需考虑 $i \in T$ 。

(1) 若 $i, j \in T$ ，则 $A_{i} + B_{j}$ 不变。

即以前能从 $i$ 访问到的点 $j$ ，现在仍能访问。

(2) 若 $i \in T, j \notin T$ ，则 $A_{i} + B_{j}$ 减小。

即以前从 $i$ 访问不到的点 $j$ ，现在有可能访问到了。

为了保证顶标符合前提条件 $\forall i,j,A_{i} + B_{j}\geq w(i,j)$ ，我们就在所有 $i\in T,j\notin T$ 的边 $(i,j)$ 之中，找出最小的 $A_{i} + B_{j} - w(i,j)$ ，作为 $\Delta$ 的值。只要原图存在完备匹配，这样的边一定存在。上述方法既不会破坏前提条件，又能保证至少有一条新的边会加入相等子图，使交错树中至少一个左部点能访问到的右部点增多。

不断重复以上过程，直到每一个左部点都匹配成功，就得到了相等子图的完备匹配，即原图的带权最大匹配。具体实现时， $\Delta$ 的值可以在DFS的过程中顺便求出。KM算法的时间复杂度为 $O(N^{3})$ 。

const int N = 105;  
int w[N][N]; // 边权  
int la[N], lb[N]; // 左、右部点的顶标  
bool va[N], vb[N]; // 访问标记：是否在交错树中  
int match[N]; // 右部点匹配了哪一个左部点  
int n, delta;  
bool dfs(int x) {  
    va[x] = 1; // 访问标记：x 在交错树中  
    for (int y = 1; y <= n; y++)  
        if (!vb[y])  
            if (la[x] + lb[y] - w[x][y] == 0) { // 相等子图  
                vb[y] = 1; // 访问标记：y 在交错树中  
                if (!match[y] || dfs(match[y])) {  
                    match[y] = x;  
                    return true;  
            }  
        else delta = min(delta, la[x] + lb[y] - w[x][y]);  
    return false;  
}  
int KM() {  
    for (int i = 1; i <= n; i++) {  
        la[i] = -(1 << 30); // -inf  
        lb[i] = 0;  
    }  
};

for (int j = 1; j <= n; j++)  
    la[i] = max(la[i], w[i][j]);  
}  
for (int i = 1; i <= n; i++)  
    while (true) { // 直到左部点找到匹配  
        memset(va, 0, sizeof(va));  
        memset(vb, 0, sizeof(vb));  
        delta = 1 << 30; // inf  
        if (dfs(i)) break;  
        for (int j = 1; j <= n; j++) { // 修改顶标  
            if (va[j]) la[j] -= delta;  
            if (vb[j]) lb[j] += delta;  
        }  
    }  
    int ans = 0;  
for (int i = 1; i <= n; i++) ans += wmatch[i][i];  
return ans;

【例题】Ants FOJ3565

平面上共有 $2*N$ 个点， $N$ 个是白点， $N$ 个是黑点。对于每个白点，找到一个黑点，把二者用线段连起来，要求最后所有线段都不相交，求一种方案。数据保证有解， $N \leq 100$ 。

题目要求最后所有线段都不相交，等价于让每条线段的长度之和最小。

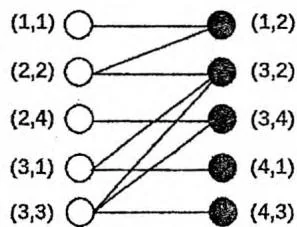
试想，如果第 $i_1$ 个白点连第 $j_1$ 个黑点，第 $i_2$ 个白点连第 $j_2$ 个黑点，并且线段 $(i_1, j_1)$ 和 $(i_2, j_2)$ 相交，那么就交换一下，让 $i_1$ 连 $j_2$ ， $i_2$ 连 $j_1$ ，这样就不会交叉，并且由三角形两边之和大于第三边可知，两条线段的长度之和一定变小。如下图所示：

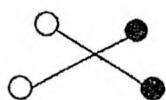
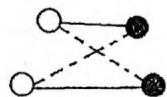
把 $N$ 个白点看作左部点， $N$ 个黑点看作右部点。 $\forall i, j$ ，让第 $i$ 个白点和第 $j$ 个黑点连边，边权 $w(i, j)$ 等于它们在平面上的距离，求二分图带权最小匹配，匹配边就是线段连接的方案（数据保证一定有解）。

注意，当用KM算法求二分图带权最小匹配时，我们把所有边权 $w(i,j)$ 取为相反数，转化为求二分图带权最大匹配，最后把 $-ans$ 作为答案即可。