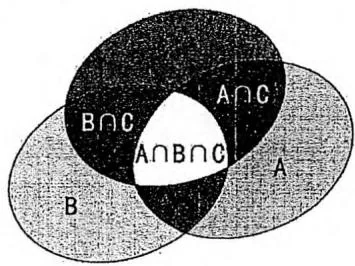
0x37 容斥原理与 Mobius 函数

容斥原理

设 $S_{1}, S_{2}, \dots, S_{n}$ 为有限集合， $|S|$ 表示集合 $S$ 的大小，则：

我们可以简单地用文氏图来宏观地描述容斥原理，如下图所示。

多重集的组合数

设 $S = \{n_{1} \cdot a_{1}, n_{2} \cdot a_{2}, \dots, n_{k} \cdot a_{k}\}$ 是由 $n_{1}$ 个 $a_{1}$ , $n_{2}$ 个 $a_{2}$ , $\dots$ , $n_{k}$ 个 $a_{k}$ 组成的多重集。设 $n = \sum_{i=1}^{k} n_{i}$ , 对于任意整数 $r \leq n$ , 从 $S$ 中取出 $r$ 个元素组成一个多重集 (不考虑顺序), 产生的不同多重集的数量为:

证明：

不考虑 $n_i$ 的限制，从 $S$ 中任选 $r$ 个元素，相当于从多重集 $\{\infty \cdot a_1, \infty \cdot a_2, \dots, \infty \cdot a_k\}$ 中取出 $r$ 个元素。根据我们在0x36节中对多重集组合数的讨论，方法数为 $C_{k+r-1}^{k-1}$ 。

设 $S_{i}$ $(1\leq i\leq k)$ 表示至少包含 $n_i + 1$ 个 $a_{i}$ 的多重集。我们先从 $s$ 中取出 $n_i + 1$ 个 $a_{i}$ ，然后再任选 $r - n_{i} - 1$ 个元素，即可构成 $S_{i}$ 。与上面同理，可以构成的不同 $S_{i}$ 的数量为 $C_{k + r - n_i - 2}^{k - 1}$

进一步地，先从 $S$ 中取出 $n_i + 1$ 个 $a_i$ 和 $n_j + 1$ 个 $a_j$ ，然后再任选 $r - n_i - n_j - 2$ 个元素，即可构成 $S_i \cap S_j$ ，方法数为：

根据容斥原理，至少有一种 $a_{i}$ 选取的数量超过 $n_i$ 限制的多重集共有：

故满足所有限制的合法多重集共有 $C_{k + r - 1}^{k - 1} - \left|\bigcup_{i = 1}^{k}S_{i}\right|$ 个，两式相减即得原命题。证毕。

【例题】Devu and Flowers Codeforces451E

Devu 有 $N$ 个盒子，第 $i$ 个盒子中有 $A_{i}$ 枝花。同一个盒子内的花颜色相同，不同盒子内的花颜色不同。Devu 要从这些盒子中选出 $M$ 枝花组成一束，求共有多少种方案。若两束花每种颜色的花的数量都相同，则认为这两束花是相同的方案。输出对 $10^{9} + 7$ 取模之后的结果即可。 $1 \leq N \leq 20, 0 \leq M \leq 10^{14}, 0 \leq A_{i} \leq 10^{12}$ 。

设第 $i$ 个盒子中的花颜色为 $C_i$ ，则本题等价于从多重集 $S = \{A_1 \cdot C_1, A_2 \cdot C_2, \dots, A_n \cdot C_n\}$ 中选出 $M$ 个元素能够产生的不同多重集的数量。根据多重集组合数的结论，本题的答案为：

在具体实现时，我们可以枚举 $x = 0\sim 2^{N} - 1$ ，若 $\pmb{x}$ 在二进制表示下共有 $\mathcal{P}$ 位为

1，分别是第 $i_1,i_2,\dots ,i_p$ 位，则这个 $\mathcal{X}$ 就代表上式中的一项：

特别地， $x = 0$ 代表 $C_{N + M - 1}^{N}$ 。这样我们就可以得到容斥原理计算多重集组合数的公式的每一项。

对于每一项组合数， $N$ 的范围很小，但 $M$ 的范围很大。我们以 $C_{N + M - 1}^{N - 1}$ 为例，因为 $C_{N + M - 1}^{N - 1} = P_{N + M - 1}^{N - 1} / (N - 1)!$ ，所以可以先计算排列数 $P_{N + M - 1}^{N - 1} = (N + M - 1) * (N + M - 2) * \dots * (M + 1)$ ，然后再乘上 $(N - 1)!$ 的乘法逆元。我们还可以应用Lucas定理，先把 $N + M - 1$ 对 $10^9 + 7$ 取模，再计算组合数，避免乘法结果超出64位整数的表示范围。

const int mod = 1000000007;  
long long a[22], m, ans = 0;  
int inv[22], n;  
int power(int a, int b) { // a^b  
    int c = 1;  
    for ( ; b; b >= 1 ) {  
        if (b&1) c = (long long)c * a % mod;  
            a = (long long)a * a % mod;  
        }  
    return c;  
}  
// C(y,x)  
int C(long long y, int x) {  
    if (y < 0 || x < 0 || y < x) return 0;  
    y % = mod;  
    if (y == 0 || x == 0) return 1;  
    int ans = 1;  
    for (int i = 0; i <= x; i++)  
        ans = (long long)ans * (y - i) % mod;  
    for (int i = 1; i <= x; i++)  
        ans = (long long)ans * inv[i] % mod;  
    return ans;

int main() {  
    for (int i = 1; i <= 20; i++)  
        inv[i] = power(i, mod-2);  
    cin >> n >> m;  
    for (int i = 1; i <= n; i++) cin >> a[i];  
    for (int x = 0; x < 1 << n; x++) {  
        if (x == 0) {  
            ans = (ans + C(n+m-1, n-1)) % mod;  
        }  
    else {  
        long long t = n + m;  
        int p = 0;  
        for (int i = 0; i < n; i++)  
            if (x >> i & 1) {  
                p++;  
                t -= a[i + 1];  
            }  
        t -= p + 1;  
        if (p&1) {  
            ans = (ans - C(t, n-1)) % mod;  
        }  
    else {  
        ans = (ans + C(t, n-1)) % mod;  
    }  
}  
cout << (ans + mod) % mod << endl;

Mobius函数

设正整数 $N$ 按照算术基本定理分解质因数为 $N = p_{1}^{c_{1}}p_{2}^{c_{2}}\dots p_{m}^{c_{m}}$ ，定义函数

称 $\mu (N)$ 为Mobius函数（莫比乌斯函数）。

通俗地讲，当 $N$ 包含相等的质因子时， $\mu (N) = 0$ 。当 $N$ 的所有质因子各不相等时，若 $N$ 有偶数个质因子， $\mu (N) = 1$ ，若 $N$ 有奇数个质因子， $\mu (N) = 0$ 。

若只求一项Mobius函数，则分解质因数即可计算。若求 $1\sim N$ 的每一项Mobius函数，可以利用Eratosthenes筛法计算。把所有 $\mu$ 值初始化为1。接下来，对于筛出的每个质数 $p$ ，令 $\mu (p) = -1$ ，并扫描 $p$ 的倍数 $x = 2p,3p,\dots ,[n / p]*p$ ，检查 $x$ 能否被 $p^2$ 整除。若能，则令 $\mu (x) = 0$ ，否则令 $\mu (x) = -\mu (x)$ 。

for (int i = 1; i <= n; i++) miu[i] = 1, v[i] = 0;  
for (int i = 2; i <= n; i++) {  
    if (v[i]) continue;  
    miu[i] = -1;  
    for (int j = 2 * i; j <= n; j++) {  
        v[j] = 1;  
        if ((j / i) % i == 0) miu[j] = 0;  
            else miu[j] *= -1;  
    }  
}

【例题】ZapBZOJ1101

有 50000 组询问，每次询问给定三个整数 $a, b, k$ ，求有多少对二元组 $(x, y)$ ，满足 $x \leq a$ ， $y \leq b$ 并且 $\gcd(a, b) = k$ 。 $1 \leq k \leq a, b \leq 50000$ 。

求有多少对二元组 $(x, y)$ 满足 $x \leq a, y \leq b$ 并且 $\gcd(a, b) = k$ ，等价于求有多少对二元组 $(x, y)$ 满足 $x \leq a / k, y \leq b / k$ 并且 $x, y$ 互质。

设 $D[a,b,k]$ 表示满足 $x \leq a, y \leq b$ 且 $k \mid \gcd(a,b)$ 的二元组有多少对。显然只要 $x,y$ 都是 $k$ 的倍数即可。 $1 \sim a$ 之间 $k$ 的倍数有 $\lfloor a / k \rfloor$ 个。故 $D[a,b,k] = \lfloor a / k \rfloor \lfloor b / k \rfloor$ 。

设 $F[a,b]$ 表示满足 $x \leq a, y \leq b$ 且 $x,y$ 互质的二元组有多少对。根据容斥原理：

上式的意思是，没有任何限制的二元组总数为 $D[a, b, 1] = a * b$ 。应当减去 $\gcd(a, b)$ 是2，3，5，…的倍数的二元组数量。这样又重复减掉了 $\gcd(a, b)$ 既是2的倍数、又是3的倍数的二元组数量，应该加回来。依此类推， $D[a, b, i]$ 的系数恰好就是Mobius函数。

回顾 $0 \times 32$ 节中例题“余数之和”的讨论，我们知道： $\forall i \in [x, \min \left( \lfloor a / \lfloor a / x \rfloor \right], \lfloor b / \lfloor b / x \rfloor \rfloor)$ ， $D[a, b, i] = \lfloor a / i \rfloor \lfloor b / i \rfloor$ 的值都相等，预处理出 Möbius 函数的前缀和，即可直接累加这一段的答案。这样的段只有 $O\left( \sqrt{a} + \sqrt{b} \right)$ 个。