0x32约数 定义
若整数 n n n d d d d d d n n n d d d n n n n n n d d d d ∣ n d \mid n d ∣ n
算术基本定理的推论
在算术基本定理中,若正整数 N N N N = p 1 c 1 p 2 c 2 … p m c m N = p_1^{c_1}p_2^{c_2}\dots p_m^{c_m} N = p 1 c 1 p 2 c 2 … p m c m c i c_{i} c i p i p_i p i p 1 < p 2 < ⋯ < p m p_1 < p_2 < \dots < p_m p 1 < p 2 < ⋯ < p m N N N
{ p 1 b 1 p 2 b 2 … p m b m } , 其 中 0 ≤ b i ≤ c i \left\{p _ {1} ^ {b _ {1}} p _ {2} ^ {b _ {2}} \dots p _ {m} ^ {b _ {m}} \right\}, \text {其 中} 0 \leq b _ {i} \leq c _ {i} { p 1 b 1 p 2 b 2 … p m b m } , 其 中 0 ≤ b i ≤ c i N N N Π \Pi Π ∑ \sum ∑
( c 1 + 1 ) ∗ ( c 2 + 1 ) ∗ ⋯ ∗ ( c m + 1 ) = ∏ i = 1 m ( c i + 1 ) (c _ {1} + 1) * (c _ {2} + 1) * \dots * (c _ {m} + 1) = \prod_ {i = 1} ^ {m} (c _ {i} + 1) ( c 1 + 1 ) ∗ ( c 2 + 1 ) ∗ ⋯ ∗ ( c m + 1 ) = i = 1 ∏ m ( c i + 1 ) N N N
( 1 + p 1 + p 1 2 + ⋯ + p 1 c 1 ) ∗ ⋯ ∗ ( 1 + p m + p m 2 + ⋯ + p m c m ) = ∏ i = 1 m ( ∑ j = 0 c i ( p i ) j ) \left(1 + p _ {1} + p _ {1} ^ {2} + \dots + p _ {1} ^ {c _ {1}}\right) * \dots * \left(1 + p _ {m} + p _ {m} ^ {2} + \dots + p _ {m} ^ {c _ {m}}\right) = \prod_ {i = 1} ^ {m} \left(\sum_ {j = 0} ^ {c _ {i}} (p _ {i}) ^ {j}\right) ( 1 + p 1 + p 1 2 + ⋯ + p 1 c 1 ) ∗ ⋯ ∗ ( 1 + p m + p m 2 + ⋯ + p m c m ) = i = 1 ∏ m ( j = 0 ∑ c i ( p i ) j ) 求 N N N
若 d ≥ N d \geq \sqrt{N} d ≥ N N N N N / d ≤ N N / d \leq \sqrt{N} N / d ≤ N N N N N \sqrt{N} N
因此,只需要扫描 d = 1 ∼ N d = 1 \sim \sqrt{N} d = 1 ∼ N d d d N N N N / d N / d N / d N N N O ( N ) O(\sqrt{N}) O ( N )
int factor[1600], m = 0;
for (int i = 1; i*i <= n; i++) {
if (n % i == 0) {
factor[++m] = i;
if (i != n/i) factor[++m] = n/i;
}
}
for (int i = 1; i <= m; i++)
cout << factor[i] << endl;试除法的推论 一个整数 N N N 2 N 2\sqrt{N} 2 N
求 1 ∼ N 1\sim N 1 ∼ N 若用“试除法”分别求出 1 ∼ N 1 \sim N 1 ∼ N O ( N N ) O(N \sqrt{N}) O ( N N ) d d d 1 ∼ N 1 \sim N 1 ∼ N d d d d d d d , 2 d , 3 d , … , ⌊ N / d ⌋ ∗ d d, 2d, 3d, \dots, \lfloor N / d \rfloor * d d , 2 d , 3 d , … , ⌊ N / d ⌋ ∗ d 1 ∼ N 1 \sim N 1 ∼ N
vector<int> factor[500010];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n/i; j++)
factor[i*j].push_back(i);
for (int i = 1; i <= n; i++) {
for (int j = 0; j < factor[i].size(); j++)
printf("%d ", factor[i][j]);
puts("");
}上述算法的时间复杂度为 O ( N + N / 2 + N / 3 + ⋯ + N / N ) = O ( N log N ) O(N + N / 2 + N / 3 + \dots +N / N) = O(N\log N) O ( N + N /2 + N /3 + ⋯ + N / N ) = O ( N log N )
倍数法的推论 1 ∼ N 1 \sim N 1 ∼ N N log N N \log N N log N
【例题】反素数 BZOJ1053 对于任何正整数 x x x g ( x ) \mathrm{g}(x) g ( x ) g ( 1 ) = 1 \mathrm{g}(1) = 1 g ( 1 ) = 1 g ( 6 ) = 4 \mathrm{g}(6) = 4 g ( 6 ) = 4
如果某个正整数 x x x 0 < i < x 0 < i < x 0 < i < x g ( x ) > g ( i ) \mathrm{g}(x) > \mathrm{g}(i) g ( x ) > g ( i ) x x x
现在给定一个数 N ( 1 ≤ N ≤ 2 ∗ 10 9 ) N(1 \leq N \leq 2 * 10^{9}) N ( 1 ≤ N ≤ 2 ∗ 1 0 9 ) N N N
引理1:
1 ∼ N 1 \sim N 1 ∼ N 1 ∼ N 1 \sim N 1 ∼ N
证明:
设 m m m 1 ∼ N 1 \sim N 1 ∼ N m m m m m m
∀ x < m \forall x < m ∀ x < m g ( x ) < g ( m ) \mathbf{g}(x) < \mathbf{g}(m) g ( x ) < g ( m )
∀ x > m , g ( x ) ≤ g ( m ) \forall x > m, \mathrm{g}(x) \leq \mathrm{g}(m) ∀ x > m , g ( x ) ≤ g ( m )
根据反质数的定义,第一条性质说明 m m m m m m m m m
引理2:
1 ∼ N 1 \sim N 1 ∼ N
证明:
因为最小的11个质数的乘积 2 ∗ 3 ∗ 5 ∗ 7 ∗ 11 ∗ 13 ∗ 17 ∗ 19 ∗ 23 ∗ 29 ∗ 31 > 2 ∗ 10 9 2*3*5*7*11*13*17*19*23*29*31 > 2*10^9 2 ∗ 3 ∗ 5 ∗ 7 ∗ 11 ∗ 13 ∗ 17 ∗ 19 ∗ 23 ∗ 29 ∗ 31 > 2 ∗ 1 0 9 N ≤ 2 ∗ 10 9 N \leq 2*10^9 N ≤ 2 ∗ 1 0 9
因为即使只包含最小的质数,仍然有 2 31 > 2 ∗ 10 9 2^{31} > 2 * 10^9 2 31 > 2 ∗ 1 0 9 N ≤ 2 ∗ 10 9 N \leq 2 * 10^9 N ≤ 2 ∗ 1 0 9
引理3:
∀ x ∈ [ 1 , N ] \forall x \in [1, N] ∀ x ∈ [ 1 , N ] x x x x x x 2 c 1 ∗ 3 c 2 ∗ 5 c 3 ∗ 7 c 4 ∗ 11 c 5 ∗ 13 c 6 ∗ 17 c 7 ∗ 19 c 8 ∗ 23 c 9 ∗ 29 c 10 2^{c_{1}} * 3^{c_{2}} * 5^{c_{3}} * 7^{c_{4}} * 11^{c_{5}} * 13^{c_{6}} * 17^{c_{7}} * 19^{c_{8}} * 23^{c_{9}} * 29^{c_{10}} 2 c 1 ∗ 3 c 2 ∗ 5 c 3 ∗ 7 c 4 ∗ 1 1 c 5 ∗ 1 3 c 6 ∗ 1 7 c 7 ∗ 1 9 c 8 ∗ 2 3 c 9 ∗ 2 9 c 10 c 1 ≥ c 2 ≥ ⋯ ≥ c 10 ≥ 0 c_{1} \geq c_{2} \geq \cdots \geq c_{10} \geq 0 c 1 ≥ c 2 ≥ ⋯ ≥ c 10 ≥ 0
通俗地讲, x x x
证明:
反证法。由引理2,若 x x x p k ( p > 29 ) p^k (p > 29) p k ( p > 29 ) p ′ p' p ′ x x x x / p k ∗ p ′ k x / p^k * p'^k x / p k ∗ p ′ k x x x x x x
同理,若 x x x x x x
综上所述,我们可以使用深度优先搜索 (DFS),尝试依次确定前10个质数的指数,并满足指数单调递减、总乘积不超过 N N N
在这两个限制条件下,搜索量实际上非常小。每当搜索出一个满足条件的整数时,我们就按照引理1的结论更新答案,最终得到约数个数最多的数中最小的一个。
【例题】余数之和 BZOJ1257
给定正整数 n n n k k k ( k m o d 1 ) + ( k m o d 2 ) + ⋯ + ( k m o d n ) (k \bmod 1) + (k \bmod 2) + \dots + (k \bmod n) ( k mod 1 ) + ( k mod 2 ) + ⋯ + ( k mod n ) 1 ≤ n , k ≤ 10 9 1 \leq n, k \leq 10^9 1 ≤ n , k ≤ 1 0 9
注意到 k m o d i = k − ⌊ k / i ⌋ ∗ i k \mod i = k - \lfloor k / i \rfloor * i k mod i = k − ⌊ k / i ⌋ ∗ i n ∗ k − ∑ i = 1 n ⌊ k / i ⌋ ∗ i n * k - \sum_{i=1}^{n} \lfloor k / i \rfloor * i n ∗ k − ∑ i = 1 n ⌊ k / i ⌋ ∗ i
对于任意整数 x ∈ [ 1 , k ] x \in [1, k] x ∈ [ 1 , k ] g ( x ) = ⌊ k / ⌊ k / x ⌋ ⌋ g(x) = \lfloor k / \lfloor k / x \rfloor \rfloor g ( x ) = ⌊ k / ⌊ k / x ⌋⌋ f ( x ) = k / x f(x) = k / x f ( x ) = k / x g ( x ) ≥ ⌊ k / ( k / x ) ⌋ = x g(x) \geq \lfloor k / (k / x) \rfloor = x g ( x ) ≥ ⌊ k / ( k / x )⌋ = x ⌊ k / g ( x ) ⌋ ≤ ⌊ k / x ⌋ \lfloor k / g(x) \rfloor \leq \lfloor k / x \rfloor ⌊ k / g ( x )⌋ ≤ ⌊ k / x ⌋
另外, ⌊ k / g ( x ) ⌋ ≥ ⌊ k / ( k / ⌊ k / x ⌋ ) ⌋ = ⌊ k / k ∗ ⌊ k / x ⌋ ⌋ = ⌊ k / x ⌋ \lfloor k / \mathrm{g}(x)\rfloor \geq \lfloor k / (k / \lfloor k / x\rfloor)\rfloor = \lfloor k / k*\lfloor k / x\rfloor \rfloor = \lfloor k / x\rfloor ⌊ k / g ( x )⌋ ≥ ⌊ k / ( k / ⌊ k / x ⌋)⌋ = ⌊ k / k ∗ ⌊ k / x ⌋⌋ = ⌊ k / x ⌋ ⌊ k / g ( x ) ⌋ = ⌊ k / x ⌋ \lfloor k / \mathrm{g}(x)\rfloor = \lfloor k / x\rfloor ⌊ k / g ( x )⌋ = ⌊ k / x ⌋
进一步可得, ∀ i ∈ [ x , ⌊ k / ⌊ k / x ⌋ ] ] \forall i\in [x,\lfloor k / \lfloor k / x\rfloor ]] ∀ i ∈ [ x , ⌊ k / ⌊ k / x ⌋]] ⌊ k / i ⌋ \lfloor k / i\rfloor ⌊ k / i ⌋
∀ i ∈ [ 1 , k ] , ⌊ k / i ⌋ \forall i \in [1, k], \lfloor k / i \rfloor ∀ i ∈ [ 1 , k ] , ⌊ k / i ⌋ 2 k 2\sqrt{k} 2 k i ≤ k i \leq \sqrt{k} i ≤ k i i i k \sqrt{k} k ⌊ k / i ⌋ \lfloor k / i \rfloor ⌊ k / i ⌋ k \sqrt{k} k i > k i > \sqrt{k} i > k [ k / i ] < k [k / i] < \sqrt{k} [ k / i ] < k ⌊ k / i ⌋ \lfloor k / i \rfloor ⌊ k / i ⌋ k \sqrt{k} k
综上所述,对于 i = 1 ∼ k i = 1\sim k i = 1 ∼ k ⌊ k / i ⌋ \lfloor k / i\rfloor ⌊ k / i ⌋ 2 k 2\sqrt{k} 2 k i ∈ [ x , ⌊ k / ⌊ k / x ⌋ ] i\in \left[x,\lfloor k / \lfloor k / x\rfloor \right] i ∈ [ x , ⌊ k / ⌊ k / x ⌋ ] ⌊ k / i ⌋ \lfloor k / i\rfloor ⌊ k / i ⌋ ⌊ k / x ⌋ \lfloor k / x\rfloor ⌊ k / x ⌋ ⌊ k / i ⌋ ∗ i = ⌊ k / x ⌋ ∗ i \lfloor k / i\rfloor *i = \lfloor k / x\rfloor *i ⌊ k / i ⌋ ∗ i = ⌊ k / x ⌋ ∗ i ⌊ k / x ⌋ \lfloor k / x\rfloor ⌊ k / x ⌋
整个算法的时间复杂度为 O ( k ) O(\sqrt{k}) O ( k )
long long n, k, ans;
int main() {
cin >> n >> k; ans = n * k;
for (int x = 1, gx; x <= n; x = gx + 1) {
gx = k/x ? min(k/(k/x), n) : n;
ans -= (k/x) * (x + gx) * (gx - x + 1) / 2;
}
cout << ans << endl;
return 0;最大公约数 定义 若自然数 d d d a a a b b b d d d a a a b b b a a a b b b a a a b b b gcd ( a , b ) \gcd(a, b) g cd( a , b )
若自然数 m m m a a a b b b m m m a a a b b b a a a b b b a a a b b b lcm ( a , b ) \operatorname{lcm}(a, b) lcm ( a , b )
同理,我们也可以定义三个数以及更多个数的最大公约数、最小公倍数。
定理 ∀ a , b ∈ N , gcd ( a , b ) ∗ lcm ( a , b ) = a ∗ b \forall a, b \in \mathbb {N}, \quad \operatorname * {g c d} (a, b) * \operatorname {l c m} (a, b) = a * b ∀ a , b ∈ N , gcd ( a , b ) ∗ lcm ( a , b ) = a ∗ b 证明:
设 d = gcd ( a , b ) , a 0 = a / d , b 0 = b / d d = \gcd (a,b), a_0 = a / d, b_0 = b / d d = g cd( a , b ) , a 0 = a / d , b 0 = b / d gcd ( a 0 , b 0 ) = 1 \gcd (a_0, b_0) = 1 g cd( a 0 , b 0 ) = 1 lcm ( a 0 , b 0 ) = a 0 ∗ b 0 \operatorname{lcm}(a_0, b_0) = a_0 * b_0 lcm ( a 0 , b 0 ) = a 0 ∗ b 0
于是 lcm ( a , b ) = lcm ( a 0 ∗ d , b 0 ∗ d ) = lcm ( a 0 , b 0 ) ∗ d = a 0 ∗ b 0 ∗ d = a ∗ b / d \operatorname{lcm}(a, b) = \operatorname{lcm}(a_0 * d, b_0 * d) = \operatorname{lcm}(a_0, b_0) * d = a_0 * b_0 * d = a * b / d lcm ( a , b ) = lcm ( a 0 ∗ d , b 0 ∗ d ) = lcm ( a 0 , b 0 ) ∗ d = a 0 ∗ b 0 ∗ d = a ∗ b / d
证毕。
九章算术·更相减损术
∀ a , b ∈ N , a ≥ b , 有 gcd ( a , b ) = gcd ( b , a − b ) = gcd ( a , a − b ) . \forall a, b \in \mathbb {N}, a \geq b \text {, 有} \operatorname * {g c d} (a, b) = \operatorname * {g c d} (b, a - b) = \operatorname * {g c d} (a, a - b). ∀ a , b ∈ N , a ≥ b , 有 gcd ( a , b ) = gcd ( b , a − b ) = gcd ( a , a − b ) . ∀ a , b ∈ N , 有 gcd ( 2 a , 2 b ) = 2 gcd ( a , b ) \forall a, b \in \mathbb {N} , \text {有} \gcd (2 a, 2 b) = 2 \gcd (a, b) ∀ a , b ∈ N , 有 g cd( 2 a , 2 b ) = 2 g cd( a , b ) 证明:
根据最大公约数的定义,后者显然成立,我们主要证明前者。
对于 a , b a, b a , b d d d d ∣ a , d ∣ b d \mid a, d \mid b d ∣ a , d ∣ b d ∣ ( a − b ) d \mid (a - b) d ∣ ( a − b ) d d d b , a − b b, a - b b , a − b a , b a, b a , b b , a − b b, a - b b , a − b a , a − b a, a - b a , a − b
证毕。
欧几里得算法
∀ a , b ∈ N , b ≠ 0 , gcd ( a , b ) = gcd ( b , a m o d b ) \forall a, b \in \mathbb {N}, b \neq 0, \quad \gcd (a, b) = \gcd (b, a \mod b) ∀ a , b ∈ N , b = 0 , g cd( a , b ) = g cd( b , a mod b ) 证明:
若 a < b a < b a < b gcd ( b , a m o d b ) = gcd ( b , a ) = gcd ( a , b ) \gcd (b,a\bmod b) = \gcd (b,a) = \gcd (a,b) g cd( b , a mod b ) = g cd( b , a ) = g cd( a , b )
若 a ≥ b a \geq b a ≥ b a = q ∗ b + r a = q * b + r a = q ∗ b + r 0 ≤ r < b 0 \leq r < b 0 ≤ r < b r = a m o d b r = a \mod b r = a mod b a , b a, b a , b d d d d ∣ a , d ∣ q ∗ b d \mid a, d \mid q * b d ∣ a , d ∣ q ∗ b d ∣ ( a − q b ) d \mid (a - qb) d ∣ ( a − q b ) d ∣ r d \mid r d ∣ r d d d b , r b, r b , r a , b a, b a , b b , a m o d b b, a \mod b b , a mod b
证毕。
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}使用欧几里得算法求最大公约数的复杂度为 O ( log ( a + b ) ) O(\log (a + b)) O ( log ( a + b ))
【例题】Hankson的趣味题 NOIP2009/CODEVS1172
有 n n n a , b , c , d a, b, c, d a , b , c , d x x x gcd ( a , x ) = c \gcd(a, x) = c g cd( a , x ) = c lcm ( b , x ) = d \operatorname{lcm}(b, x) = d lcm ( b , x ) = d n ≤ 2000 , 1 ≤ a , b , c , d ≤ 2 ∗ 10 9 n \leq 2000, 1 \leq a, b, c, d \leq 2 * 10^9 n ≤ 2000 , 1 ≤ a , b , c , d ≤ 2 ∗ 1 0 9
解法一 从 lcm ( b , x ) = d \operatorname{lcm}(b, x) = d lcm ( b , x ) = d x x x d d d d d d O ( n d log d ) O(n\sqrt{d}\log d) O ( n d log d )
我们提到过,虽然 d d d d \sqrt{d} d 1 ∼ d 1 \sim d 1 ∼ d log d \log d log d 10 9 10^9 1 0 9
为了尽量避免试除法中不能整除时耗费的时间,我们预处理出 1 ∼ 2 ∗ 10 9 1 \sim \sqrt{2 * 10^9} 1 ∼ 2 ∗ 1 0 9 d d d
解法二 因为 x x x d d d x x x d d d d d d p p p x x x p p p
设 a , b , c , d , x a, b, c, d, x a , b , c , d , x m a , m b , m c , m d , m x m_{a}, m_{b}, m_{c}, m_{d}, m_{x} m a , m b , m c , m d , m x p p p m x m_{x} m x
根据最大公约数的定义,在 gcd ( a , x ) = c \gcd (a,x) = c g cd( a , x ) = c
若 m a > m c m_{a} > m_{c} m a > m c m x m_{x} m x m c m_{c} m c
若 m a = m c m_{a} = m_{c} m a = m c m x ≥ m c m_{x} \geq m_{c} m x ≥ m c
若 m a < m c m_{a} < m_{c} m a < m c m x m_{x} m x
同理,根据最小公倍数的定义,在 lcm ( b , x ) = d \operatorname{lcm}(b,x) = d lcm ( b , x ) = d
若 m b < m d m_{b} < m_{d} m b < m d m x m_{x} m x m d m_{d} m d
若 m b = m d m_{b} = m_{d} m b = m d m x ≤ m d m_{x} \leq m_{d} m x ≤ m d
若 m h > m d m_h > m_d m h > m d m x m_x m x
结合两种情况,有以下结论:
当 m a = m c = m b = m d m_{a} = m_{c} = m_{b} = m_{d} m a = m c = m b = m d m x m_{x} m x m x m_{x} m x
当 m a > m c m_{a} > m_{c} m a > m c m b < m d m_{b} < m_{d} m b < m d m c ≤ m d m_{c} \leq m_{d} m c ≤ m d m x m_{x} m x m c ∼ m d m_{c} \sim m_{d} m c ∼ m d m d − m c + 1 m_{d} - m_{c} + 1 m d − m c + 1 m x m_{x} m x
我们把 m x m_x m x c n t p cnt_p c n t p x x x p p p c n t p cnt_p c n t p x x x
∏ 质 数 p ∣ d c n t p \prod_ {\text {质 数} p | d} c n t _ {p} 质 数 p ∣ d ∏ c n t p 为了更高效地计算,可以预处理出 1 ∼ 2 ∗ 10 9 1 \sim \sqrt{2 * 10^9} 1 ∼ 2 ∗ 1 0 9 d d d c n t p cnt_p c n t p d d d d d d c n t d cnt_d c n t d d d d d d d O ( n d / log d ) O(n \sqrt{d} / \log d) O ( n d / log d )
互质与欧拉函数 定义
∀ a , b ∈ N \forall a, b \in \mathbb{N} ∀ a , b ∈ N gcd ( a , b ) = 1 \gcd(a, b) = 1 g cd( a , b ) = 1 a , b a, b a , b
对于三个数或更多个数的情况,我们把 gcd ( a , b , c ) = 1 \gcd(a, b, c) = 1 g cd( a , b , c ) = 1 a , b , c a, b, c a , b , c gcd ( a , b ) = gcd ( a , c ) = gcd ( b , c ) = 1 \gcd(a, b) = \gcd(a, c) = \gcd(b, c) = 1 g cd( a , b ) = g cd( a , c ) = g cd( b , c ) = 1 a , b , c a, b, c a , b , c
欧拉函数
1 ∼ N 1\sim N 1 ∼ N N N N φ ( N ) \varphi (N) φ ( N )
若在算术基本定理中, N = p 1 c 1 p 2 c 2 … p m c m N = p_{1}^{c_{1}}p_{2}^{c_{2}}\dots p_{m}^{c_{m}} N = p 1 c 1 p 2 c 2 … p m c m
φ ( N ) = N ∗ p 1 − 1 p 1 ∗ p 2 − 1 p 2 ∗ ⋯ ∗ p m − 1 p m = N ∗ ∏ 质 数 p ∣ N ( 1 − 1 p ) \varphi (N) = N * \frac {p _ {1} - 1}{p _ {1}} * \frac {p _ {2} - 1}{p _ {2}} * \dots * \frac {p _ {m} - 1}{p _ {m}} = N * \prod_ {\text {质 数} p | N} \left(1 - \frac {1}{p}\right) φ ( N ) = N ∗ p 1 p 1 − 1 ∗ p 2 p 2 − 1 ∗ ⋯ ∗ p m p m − 1 = N ∗ 质 数 p ∣ N ∏ ( 1 − p 1 ) 证明:
设 p p p N N N 1 ∼ N 1 \sim N 1 ∼ N p p p p , 2 p , 3 p , … , ( N / p ) ∗ p p, 2p, 3p, \dots, (N / p) * p p , 2 p , 3 p , … , ( N / p ) ∗ p N / p N / p N / p q q q N N N 1 ∼ N 1 \sim N 1 ∼ N q q q N / q N / q N / q N / p + N / q N / p + N / q N / p + N / q p ∗ q p * q p ∗ q 1 ∼ N 1 \sim N 1 ∼ N N N N p p p q q q
N − N p − N q + N p q = N ∗ ( 1 − 1 p − 1 q + 1 p q ) = N ( 1 − 1 p ) ( 1 − 1 q ) N - \frac {N}{p} - \frac {N}{q} + \frac {N}{p q} = N * \left(1 - \frac {1}{p} - \frac {1}{q} + \frac {1}{p q}\right) = N \left(1 - \frac {1}{p}\right) \left(1 - \frac {1}{q}\right) N − p N − q N + pq N = N ∗ ( 1 − p 1 − q 1 + pq 1 ) = N ( 1 − p 1 ) ( 1 − q 1 ) 实际上,上述思想被称为容斥原理,我们将在0x37节详细介绍。类似地,可以在 N N N 1 ∼ N 1\sim N 1 ∼ N N N N N N N
证毕。
根据欧拉函数的计算式,我们只需要分解质因数,即可顺便求出欧拉函数。
int phi(int n) { int ans $=$ n; for (int i = 2; i <= sqrt(n); i++) if $(n \% i == 0)$ { ans $=$ ans / i \* (i-1); while $(n \% i == 0)$ n /= i; } if $(n > 1)$ ans $=$ ans / n \* (n-1); return ans; }性质 1 ∼ 2 1\sim 2 1 ∼ 2
∀ n > 1 \forall n > 1 ∀ n > 1 1 ∼ n 1\sim n 1 ∼ n n n n n ∗ φ ( n ) / 2 n*\varphi (n) / 2 n ∗ φ ( n ) /2
若 a , b a, b a , b φ ( a b ) = φ ( a ) φ ( b ) \varphi(ab) = \varphi(a)\varphi(b) φ ( ab ) = φ ( a ) φ ( b )
证明:
因为 gcd ( n , x ) = gcd ( n , n − x ) \gcd (n,x) = \gcd (n,n - x) g cd( n , x ) = g cd( n , n − x ) n n n x , n − x x, n - x x , n − x n / 2 n / 2 n /2 n n n n / 2 n / 2 n /2
根据欧拉函数的计算式,对 a , b a, b a , b
证毕。
积性函数 如果当 a , b a, b a , b f ( a b ) = f ( a ) ∗ f ( b ) f(ab) = f(a)*f(b) f ( ab ) = f ( a ) ∗ f ( b ) f f f
性质3~6
若 f f f n = ∏ i = 1 m p i c i n = \prod_{i=1}^{m} p_i^{c_i} n = ∏ i = 1 m p i c i f ( n ) = ∏ i = 1 m f ( p i c i ) f(n) = \prod_{i=1}^{m} f\left(p_i^{c_i}\right) f ( n ) = ∏ i = 1 m f ( p i c i )
若 p ∣ n p \mid n p ∣ n p 2 ∣ n p^2 \mid n p 2 ∣ n φ ( n ) = φ ( n / p ) ∗ p 10 \varphi(n) = \varphi(n / p) * p^{10} φ ( n ) = φ ( n / p ) ∗ p 10
若 p ∣ n p \mid n p ∣ n p 2 ∤ n p^2 \nmid n p 2 ∤ n φ ( n ) = φ ( n / p ) ∗ ( p − 1 ) \varphi(n) = \varphi(n / p) * (p - 1) φ ( n ) = φ ( n / p ) ∗ ( p − 1 )
∑ d ∣ n φ ( d ) = n \sum_{d|n}\varphi (d) = n ∑ d ∣ n φ ( d ) = n
证明:
把 n n n
若 p ∣ n p|n p ∣ n p 2 ∣ n p^2 |n p 2 ∣ n n , n / p n,n / p n , n / p P \mathcal{P} P φ ( n ) \varphi (n) φ ( n ) φ ( n / p ) \varphi (n / p) φ ( n / p ) P \mathcal{P} P
若 p ∣ n p \mid n p ∣ n p 2 ∤ n p^2 \nmid n p 2 ∤ n n , n / p n, n / p n , n / p φ \varphi φ φ ( n ) = φ ( n / p ) ∗ φ ( p ) \varphi(n) = \varphi(n / p) * \varphi(p) φ ( n ) = φ ( n / p ) ∗ φ ( p ) φ ( p ) = p − 1 \varphi(p) = p - 1 φ ( p ) = p − 1
设 f ( n ) = ∑ d ∣ n φ ( d ) f(n) = \sum_{d\mid n}\varphi (d) f ( n ) = ∑ d ∣ n φ ( d ) φ \varphi φ n , m n,m n , m f ( n m ) = ∑ d ∣ n m φ ( d ) = ( ∑ d ∣ n φ ( d ) ) ∗ ( ∑ d ∣ m φ ( d ) ) = f ( n ) ∗ f ( m ) f(nm) = \sum_{d\mid nm}\varphi (d) = \left(\sum_{d\mid n}\varphi (d)\right)*\left(\sum_{d\mid m}\varphi (d)\right) = f(n)*f(m) f ( nm ) = ∑ d ∣ nm φ ( d ) = ( ∑ d ∣ n φ ( d ) ) ∗ ( ∑ d ∣ m φ ( d ) ) = f ( n ) ∗ f ( m ) ∑ d ∣ n φ ( d ) \sum_{d\mid n}\varphi (d) ∑ d ∣ n φ ( d ) f ( p m ) = ∑ d ∣ p m φ ( d ) = φ ( 1 ) + φ ( p ) + f(p^{m}) = \sum_{d\mid p^{m}}\varphi (d) = \varphi (1) + \varphi (p) + f ( p m ) = ∑ d ∣ p m φ ( d ) = φ ( 1 ) + φ ( p ) + φ ( p 2 ) + ⋯ + φ ( p m ) \varphi (p^2) + \dots +\varphi (p^m) φ ( p 2 ) + ⋯ + φ ( p m ) p m p^m p m f ( n ) = f(n) = f ( n ) = \prod_{i = 1}^{m}f\bigl {(}p_i^{c_i}\bigr) = \prod_{i = 1}^{m}p_i^{c_i} = n
证毕。
有关积性函数还有许多内容,并可延伸出狄利克雷卷积、莫比乌斯反演以及一系列相关的快速求和问题。这些内容比较高深,超出了我们的探讨范围,学有余力的读者可
以自行查阅相关资料。
【例题】VisibleLatticePoints FOJ3090
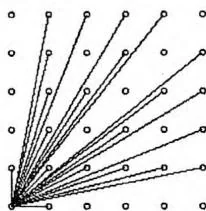
在一个平面直角坐标系的以 ( 0 , 0 ) (0,0) ( 0 , 0 ) ( N , N ) (N,N) ( N , N ) ( 0 , 0 ) (0,0) ( 0 , 0 )
求在原点向四周看去,能够看到多少个钉子。一个钉子能被看到,当且仅当连接它和原点的线段上没有其他钉子。右图也画出了所有能看到的钉子以及视线。 1 ≤ N ≤ 1000 1 \leq N \leq 1000 1 ≤ N ≤ 1000
分析题目容易发现,除了(1,0)、(0,1)和(1,1)这三个钉子外,一个钉子 ( x , y ) (x,y) ( x , y ) 1 ≤ x , y ≤ N 1\leq x,y\leq N 1 ≤ x , y ≤ N x ≠ y x\neq y x = y gcd ( x , y ) = 1 \gcd (x,y) = 1 g cd( x , y ) = 1
在 1 ≤ x , y ≤ N , x ≠ y 1 \leq x, y \leq N, x \neq y 1 ≤ x , y ≤ N , x = y ( 0 , 0 ) (0,0) ( 0 , 0 ) ( N , N ) (N,N) ( N , N ) 1 ≤ x < y ≤ N 1 \leq x < y \leq N 1 ≤ x < y ≤ N 2 ≤ y ≤ N 2 \leq y \leq N 2 ≤ y ≤ N x x x 1 ≤ x < y 1 \leq x < y 1 ≤ x < y gcd ( x , y ) = 1 \gcd(x,y) = 1 g cd( x , y ) = 1 x x x φ ( y ) \varphi(y) φ ( y )
综上所述,本题的答案就是 3 + 2 ∗ ∑ i = 2 N φ ( i ) 3 + 2*\sum_{i = 2}^{N}\varphi (i) 3 + 2 ∗ ∑ i = 2 N φ ( i ) 2 ∼ N 2\sim N 2 ∼ N
利用Eratosthenes筛法,我们可以按照欧拉函数的计算式,在 O ( N log N ) O(N\log N) O ( N log N ) 2 ∼ N 2\sim N 2 ∼ N
void euler(int n) {
for (int i = 2; i <= n; i++) phi[i] = i;
for (int i = 2; i <= n; i++)
if (phi[i] == i)
for (int j = i; j <= n; j++)
phi[j] = phi[j] / i * (i - 1);
}至此,本题已经得到解决。不过我们还可以进一步优化,利用线性筛法的思想在 O ( N ) O(N) O ( N ) 2 ∼ N 2\sim N 2 ∼ N
由前面提到的性质4和性质5:
若 p ∣ n p \mid n p ∣ n p 2 ∣ n {p}^{2} \mid n p 2 ∣ n φ ( n ) = φ ( n / p ) ∗ p \varphi \left( n\right) = \varphi \left( {n/p}\right) * p φ ( n ) = φ ( n / p ) ∗ p
若 p ∣ n p \mid n p ∣ n p 2 ∤ n p^2 \nmid n p 2 ∤ n φ ( n ) = φ ( n / p ) ∗ ( p − 1 ) \varphi(n) = \varphi(n / p) * (p - 1) φ ( n ) = φ ( n / p ) ∗ ( p − 1 )
在线性筛法中,每个合数 n n n p p p φ ( n / p ) \varphi(n / p) φ ( n / p ) φ ( n ) \varphi(n) φ ( n )
int v[MAX_N], prime[MAX_N], phi[MAX_N];
void euler(int n) {
memset(v, 0, sizeof(v)); // 最小质因子
m = 0; // 质数数量
for (int i = 2; i <= n; i++) {
if (v[i] == 0) { // i是质数
v[i] = i, prime[++m] = i;
phi[i] = i - 1;
}
// 给当前的数i乘上一个质因子
for (int j = 1; j <= m; j++) {
// i有比prime[j]更小的质因子,或者超出n的范围
if (prime[j] > v[i] || prime[j] > n / i) break;
// prime[j]是合数i*prime[j]的最小质因子
v[i*prime[j]] = prime[j];
phi[i*prime[j]] = phi[i]
*(i%prime[j] ? prime[j]-1 : prime[j]);
}
}