8._矩阵相似

矩阵相似

定义 设 $A, B$ 都是 $n$ 阶矩阵, 若有可逆矩阵 $P$, 使

则称 $B$ 是 $A$ 的相似矩阵，记做$A \sim B$, 或者说矩阵 $A$ 与 $B$ 相似. 对 $A$ 进行运算 $P^{-1} A P$ 称为对$\boldsymbol{A}$ 进行相似变换。

可逆矩阵 $P$ 称为把 $\boldsymbol{A}$ 变成 $\boldsymbol{B}$ 的相似变换矩阵.

既然定义有了，现在有一个问题：给你一个矩阵$A$，如何求的他的相似矩阵$B$和$P$， 此时前面学的特征值和特征向量的作用就可以用上了。换句话说，学习特征值与特征向量，是为这里做准备的。

矩阵相似的求法

例 求 $A=\left(\begin{array}{ccc}7 & -1 & 7 \\ 2 & -1 & -5 \\ 4 & -8 & 7\end{array}\right)$ 的相似矩阵

解：只需求 1 个相似矩阵时，不妨令 $P=\left[\begin{array}{lll}1 & & \\ & 1 & \\ & & 2\end{array}\right](|P| \neq 0)$ ， 则 $\left[\begin{array}{lll}1 & & \\ & 1 & \\ & & 2\end{array}\right]\left[\begin{array}{ccc}7 & -1 & 7 \\ 2 & -1 & -5 \\ 4 & -8 & 7\end{array}\right]\left[\begin{array}{lll}1 & & \\ & 1 & \\ & & 1/2\end{array}\right]$ 即为所球

若需求所有的相似矩阵，对于矩阵 $P$ 满足 $|P| \neq 0$ $\frac{p^*}{|p|} A P$ 即为所求 $\left(p^*=p^{-1}|p|\right)$

从这里可以看到，如果任给一个矩阵$A$，要求他的相似矩阵，可以有无数个，因此，单纯的说求一个矩阵的相似矩阵，意义不大。

但是，如果我们把B限制为对角形矩阵，则情况立刻不一样，此时变换唯一，且可求解

矩阵相似对角形的求法

先给一个公式,后面 矩阵与对角形相似 会介绍，

把上面这个公式稍微变形一下，左乘$P$,右乘 $P^{-1}$，就得到

这说明任意给一个矩阵A，可以找到一个对角形矩阵$\Lambda$ （有些找不到）, 接下来一个问题，怎么找到这里的$P$和$\Lambda$ ？ 答案就是特征值与特征向量。

例 设矩阵

求他的相似矩阵$P$和$\Lambda$

解: 先求 $A$ 的特征值．

所以 $A$ 的特征值为 $\lambda_1=-1, \lambda_2=\lambda_3=2$ ． 再求 $A$ 的特征向量． 当 $\lambda_1=-1$ 时，解方程 $(A+E) x=0$ ．由

得对应的特征向量

当 $\lambda_2=\lambda_3=2$ 时，解方程 $( A -2 E ) x = 0$ ．由

得对应的线性无关特征向量

分析上面的结论：

通过上面的解，我们找到3个特征值和3个特征向量：

$\lambda_1=-1, \lambda_2=\lambda_3=2$

我们只要把他们按照对应的位置排好即可，就可以找到相似矩阵。

排法1：使用 $\lambda_1=-1, \lambda_2=\lambda_3=2$ 即 若记

这样$A$就可以表示为 $A=P_1 \Lambda_1 P_1^{-1}$

排法2：使用 $\lambda_2=\lambda_3=2,\lambda_1=-1,$ 排列，若记

这样$A$就可以表示为 $A=P_2 \Lambda_2 P_2^{-1}$

可以看到，因为排法不同，其结果也不同，但是本质是一样的。

相似的几何意义

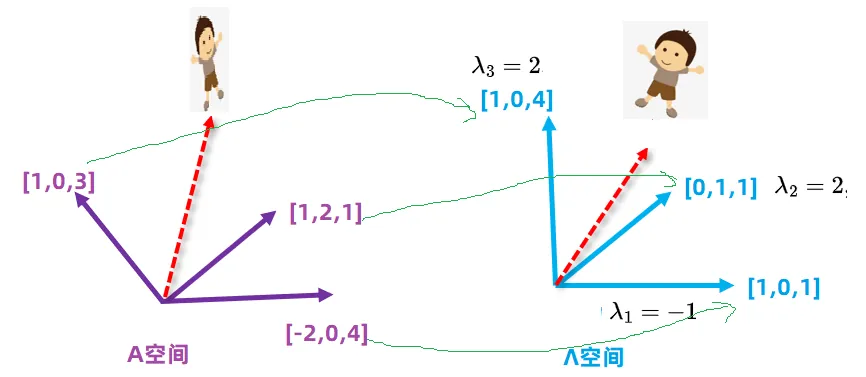
想在捋一捋矩阵相似的几何有意义，我们说过，一个矩阵相当于一个坐标系（不是坐标系里的值）， 你原来在$A$空间，通过相似映射后，你变成了$\Lambda$ 空间， 在$\Lambda$的空间里，因为 $\lambda_1=-1$ 所以，沿$x$方向方向相反，而 $\lambda_2=2, \lambda_3=2$， 所以，沿着$y,z$方向，进行了拉伸，参考下图。

通过变换后，下图右图小男孩看起来就漂亮多了

所以，矩阵相似可以理解为换个空间角度观察人物，而特征向量相当于找到了一个新的空间，特征值是新空间对应维度的伸缩率。

矩阵相似的一些定理

定理 1

若 $n$ 阶矩阵 $A$ 与 $B$ 相似，则 $A$ 与 $B$ 有相同的特征多项式，从而 $A$ 与 $B$ 有相同的特征值. 证明 因 $\boldsymbol{A}$ 与 $\boldsymbol{B}$ 相似，即有可逆矩阵 $P$ ，使 $\boldsymbol{P}^{-1} \boldsymbol{A P}=\boldsymbol{B}$, 故

推论

若 $n$ 阶矩阵 $A$ 与对角阵

相似,则 $\lambda_1, \lambda_2, \cdots, \lambda_n$ 即是 $A$ 的 $n$ 个特征值. 证明:若 $n$ 阶矩阵 $A$ 与 $B$ 相似，即 $P^{-1} A P=B$ ，则 $A^k=\left(P B P^{-1}\right)^k=P B^k P^{-1}$ ，并且 $A$ 的多项式

特别地，若有可逆矩阵 $P$ ，使 $P^{-1} A P=\Lambda$ 为对角阵，则$A^k=P \Lambda^k P^{-1}, \varphi(A)=P\varphi(\Lambda) P^{-1}$

而对于对角阵 $\Lambda=\operatorname{diag}\left(\lambda_1, \lambda_2, \cdots, \lambda_n\right)$ ，有

由此可方便地计算 ${\boldsymbol{A}}$ 的高次幕 $\boldsymbol{A}^{\bar{k}}$ 及 $\boldsymbol{A}$ 的多项式 $\bar{\varphi}({\boldsymbol{A}})$.

推广

设 $f(\lambda)$ 是矩阵 $\boldsymbol{A}$ 的特征多项式,则

这个结论的证明比较困难，但若 $A$ 与对角阵相似，则容易证明此结论. 这是因为: 若 $A$ 与对角阵相似，即有可逆矩阵 $P$ ，使 $P^{-1} A P=\Lambda=\operatorname{diag}\left(\lambda_1, \lambda_2, \cdots, \lambda_n\right)$ ，其中 $\lambda_i$ 为 $\boldsymbol{A}$ 的特征值，有 $f\left(\lambda_i\right)=0$. 于是由上面的讨论可得:

矩阵相似的性质

1．相似矩阵的行列式相同

若 $A$ 和 $B$ 相似，则：$A$ 和 $B$ 的行列式值相同； $\operatorname{Det}(A)=\operatorname{Det}(B)$ ，也记作：$|A|=|B|$ 。

2．相似矩阵的特征值相同

若 $A$ 和 $B$ 相似，则：$A$ 和 $B$ 的特征方程相同；

这意味着：$A$ 和 $B$ 的特征值（特征根）相同。

注意：特征值相同，不意味着对应的特征向量相同

3．相似矩阵的秩相同

若 $A$ 和 $B$ 相似，则：$A$ 和 $B$ 的秩相同。 $r(A)=r(B)$

4．相似矩阵的迹相同

若A和B相似，则：$A$ 和 $B$ 的迹相同；

矩阵（方阵）的迹为主对角线元素之和； $\operatorname{tr}(A)=\operatorname{tr}(B)$

5．相似矩阵的可逆性相同 若A和B相似，则：A和B的可逆性相同；

若 $A$ 可逆，则 $B$ 也可逆。若 $B$ 可逆，则 $A$ 也可逆； 若 $A$ 不可逆，则 $B$ 也不可逆。若 $B$ 不可逆，则 $A$ 也不可逆。

6．相似矩阵的可对角化性相同 如果矩阵A可对角化，那么和它相似的所有矩阵也都可以对角化。

7．相似的传递性 若 $A$ 相似于 $B$ ，而 $B$ 相似于 $C$ ，则 $A$ 相似于 $C$ 。

例题

例已知矩阵 $A =\left[\begin{array}{ccc}-2 & 0 & 0 \\ 2 & x & 2 \\ 3 & 1 & 1\end{array}\right]$ 与 $B =\left[\begin{array}{ccc}-1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & y\end{array}\right]$ 相似，求 $x$ 与 $y$ 的值．

解 由题意， $A$ 与 $B$ 相似，相似矩阵有相同的特征多项式．我们可由此来求解：

即

比较两边同次幂的系数，可求出 $x=0, y=-2$ ．

例已知二阶方阵 $A$ 的两个特征值为 $\lambda_1=1, \lambda_2=2$ ，其对应的特征向量分别为 $x_1=\left[\begin{array}{l}1 \\ 1\end{array}\right], x_2=\left[\begin{array}{c}1 \\ -1\end{array}\right]$ ，试求 $A^{2014}$ ．

解：由 $A x_1=\lambda_1 x_1, A x_2=\lambda_2 x_2$ ，可知

因此可知 $A=\left[\begin{array}{ll}x_1 & x_2\end{array}\right]\left[\begin{array}{cc}\lambda_1 & 0 \\ 0 & \lambda_2\end{array}\right]\left[\begin{array}{ll}x_1 & x_2\end{array}\right]^{-1}$ ，

例已知 $\xi =[1,1,-1]^{ T }$ 是矩阵 $A =\left[\begin{array}{ccc}2 & -1 & 2 \\ 5 & a & 3 \\ -1 & b & -2\end{array}\right]$ 的一个特征向量． （1）确定参数 $a, b$ 及 $\xi$ 对应的特征值 $\lambda$ ； （2） $A$ 是否相似于对角矩阵？说明理由．

解（1）设 $A$ 的特征向量 $\xi$ 所对应的特征值为 $\lambda$ ，则有 $A \xi =\lambda \xi$ ，即

即

解得 $\lambda=-1, a=-3, b=0$ ． （2）当 $a=-3, b=0$ 时，令

可知 $\lambda=-1$ 是 $A$ 的三重特征值，但

当 $\lambda=-1$ 时，对应的线性无关特征向量只有一个，因此 $A$ 不能相似于对角矩阵．

相似的几何意义

对于初学者而言，看到矩阵相似会很疑惑，为什么要给出这个定义。其实，矩阵相似反应的是从不同“视角（坐标系）”里查看同一个视图。 比如，有一张照片，可以从不同视角进行观看，如果把每一个视角视为一个矩阵“基”，那么这些视角(矩阵)就是相似的。

在这些视角里，会有一个比较好的视角(矩阵)，如下图，毫无疑问 B图效果最好，因为他不失真，而我们要做的工作是：给你一个矩阵，怎么找到最好的“基坐标”。

{width=500px}

关于矩阵相似的几何意义更详细介绍，请参考下一节 矩阵相似的几何意义