18._约当Jordan标准型

约当Jordan标准型

我们知道，并不是每一个 nn 阶矩阵 AA 都可以对角化．但是，我们可以证明，AA 一定能与另一种结构较简单的约当形矩阵相似。由于相关理论证明较复杂，我们只介绍与约当标准形有关的结论。

Jordan标准型

形如

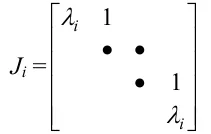
Ji=[λi1λi1⋱⋱⋱1λi]J_i=\left[\begin{array}{ccccc} \lambda_i & 1 & & & \\ & \lambda_i & 1 & & \\ & & \ddots & \ddots & \\ & & & \ddots & 1 \\ & & & & \lambda_i \end{array}\right]

的方阵，称为特征值 λi\lambda_i 的约当块．而称主对角线上为若干个约当块的分块矩阵

J=[J1J2⋱Js]J=\left[\begin{array}{llll} J_1 & & & \\ & J_2 & & \\ & & \ddots & \\ & & & J_s \end{array}\right]

（其中 Ji(i=1,2,⋯ ,s)J_i(i=1,2, \cdots, s) 为约当块）

为约当形矩阵，或约当标准形． 例如，

[210021002],[010001000],[−110−1]\left[\begin{array}{lll} 2 & 1 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 2 \end{array}\right],\left[\begin{array}{lll} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{rr} -1 & 1 \\ 0 & -1 \end{array}\right]

都是约当块．显然，约当形矩阵是一种特殊的上三角形矩阵，其特征值就是卉主对角线上的全部元素。由于一个元素可以看作一个一阶约当块，所以，对角矩阵实际上就是主对角线上全为一阶约当块的约当形矩阵。

我们不加证明地给出如下结论： 定理

在复数范围内，任一 nn 阶矩阵 AA 都相似于一个约当形矩阵 JJ ，即存在可逆矩阵 PP ，使得 P−1AP=J.JP^{-1} A P=J . J 的主对角线上的元素恰好是 AA 的特征值，并且在 JJ 的主对角线上 AA 的任一特征值出现的次数等于该特征值的重数．

约当Jordan标准型的简单解释

对于一个方程，如果有P−1AP=ΛP^{-1}AP= \Lambda 就说他是相似对角形，但是 假设 AA 有 ss 个无关的特征向量，则它与有 ss 个方块的对角形矩阵相似，每个方块有一个特征值在对角线。 图片 换句话说，我们可以把Jordan标准型 理解为分块矩阵 比如下面的矩阵

[210000020000005000000010000001000000]\left[\begin{array}{llllll} 2 & 1 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right]

是一个六阶约当形矩阵，它由三个约当块组成（把他进行分解）。

Jordan在实际计算上也不流行，而且它的计算也不稳定，AA的一点轻微变化就会分离重复的特征值，并且移除非对角线, 因此使用的并不多，稍微了解即可。

矩阵为什么对角化

矩阵对角化本质是找到一组正交坐标系，使矩阵作用简化为各坐标轴方向的伸缩变换

矩阵对角化的通俗解释可以从“换坐标系”的角度理解，目的是让复杂的矩阵运算变得像“数数”一样简单。以下是分步说明：

为什么需要“对角化”

想象你有一个遥控器（矩阵），每个按键控制不同的功能（矩阵的列）。但遥控器设计得太复杂，按下按键时多个功能同时触发（矩阵运算混乱）。 对角化的目标：重新设计遥控器，让每个按键只控制一个独立功能（矩阵运算简化为缩放）。 对角矩阵就像一个“完美遥控器”，每个按键只负责放大或缩小某个信号，互不干扰。

对角化的核心步骤

  1. 找特征向量（新坐标轴） 特征向量是矩阵变换中方向不变的向量。例如，旋转矩阵的特征向量是旋转轴，拉伸矩阵的特征向量是拉伸方向。 特征值：对应方向上的缩放比例（比如拉伸2倍，缩放0.5倍）。

  2. 用特征向量组成新基（新遥控器按键） 将特征向量排成矩阵 PP，相当于建立一组新坐标系。例如，原坐标系是直角坐标系，新坐标系可能是倾斜的，但更符合矩阵的“性格”。

  3. 对角矩阵（简化后的遥控器） 通过 P−1AP=ΛP^{-1}AP = \Lambda，原矩阵 A A 被转化为对角矩阵 Λ\Lambda，对角线上的元素就是特征值。此时，矩阵运算（如求幂）只需对每个特征值单独操作。

通俗类比

  1. 陀螺旋转 • 原坐标系下，陀螺的运动轨迹复杂。 • 若以旋转轴为新坐标系，陀螺的运动只是绕轴旋转，其他方向无变化（对角矩阵的“缩放”效果）。

  2. 遥控器优化 • 原遥控器按键混乱（普通矩阵）。 • 对角化后，每个按键只控制音量、频道等单一功能（对角矩阵的独立缩放）。

对角化的意义

  1. 简化计算 • 计算矩阵的100次幂：对角矩阵只需对每个特征值取100次幂，普通矩阵需连乘100次。 • 例子：计算 A100A^{100}，若 A=PDP−1A = PDP^{-1}，则 A100=PD100P−1 A^{100} = PD^{100}P^{-1}。

  2. 揭示本质 • 特征值代表矩阵的“核心作用力”（如量子力学中的能量本征值）。 • 特征向量代表“作用方向”（如力学中的主应力方向）。

  3. 解决实际问题 • 图像处理：PCA通过协方差矩阵对角化提取图像主特征。 • 微分方程：将方程组解耦为独立方程，便于求解。

什么矩阵能对角化？

• 实对称矩阵：必可对角化，且特征向量正交（如力学中的应力矩阵）。 • 一般矩阵：需满足有 nn 个线性无关的特征向量（如非重复特征值的矩阵）。

总之，矩阵对角化就像给矩阵“换一副眼镜”，让它原本模糊的作用变得清晰可见。通过找到最自然的坐标系（特征向量基），复杂变换被分解为简单的缩放操作。无论是量子力学中的粒子行为，还是抖音推荐算法中的用户兴趣分析，对角化都在背后默默简化问题。

实对称矩阵的对角化

在矩阵里，介绍了矩阵的转置，矩阵的转置最主要的作用就是判断一个矩阵是不是对称矩阵。 如果矩阵AA是对称矩阵，那么AT=AA^T=A，反之，如果AT=AA^T=A，那么这个矩阵是对称矩阵。 ，而二次型就是对称矩阵，所以，此时矩阵的转置就派上了用场。

定理1 不是每个矩阵都可以对角化，但是实对称矩阵一定可以对角化。这句话另外一个表述是：一个 n×nn \times n 矩阵 AA 可正交对角化的充分必要条件是 AA 是对称矩阵.

证明略。

这个定理相当奇妙，我们很难推断一个矩阵可以对角化，但是每个对称矩阵却可以对角化。即每个对称矩阵D都可以相似对角形

D∼[λ110λ22⋱0λnn]D \sim \left[\begin{array}{cccc} \lambda_{11} & & & 0 \\ & \lambda_{22} & & \\ & & \ddots & \\ 0 & & & \lambda_{n n} \end{array}\right]

我们为什么特别关心实对称矩阵？我们看一下相似与合同 合同是 CTAC=BC^TAC=B 相似是 C−1AC=BC^{-1}AC=B 仔细看，如果CT=C−1C^T=C^{-1} 多好啊，这样就又相似又合同，还真有，那就是正交相似，详见 附录2

例题

例 对角化矩阵 A=[6−2−1−26−1−1−15]A=\left[\begin{array}{rrr}6 & -2 & -1 \\ -2 & 6 & -1 \\ -1 & -1 & 5\end{array}\right]. 解：不难发现，这是一个对称矩阵。 AA 的特征方程是

0=−λ3+17λ2−90λ+144=−(λ−8)(λ−6)(λ−3)0=-\lambda^3+17 \lambda^2-90 \lambda+144=-(\lambda-8)(\lambda-6)(\lambda-3)

通过标准计算可得到每个特征子空间的一个基 ①当 λ=8\lambda=8 ,特征向量为

α1=[−110]\alpha_1=\left[\begin{array}{r} -1 \\ 1 \\ 0 \end{array}\right]

②当 λ=6\lambda=6 ,特征向量为

α2=[−1−12]\alpha_2=\left[\begin{array}{r} -1 \\ -1 \\ 2 \end{array}\right]

③ 当 λ=3\lambda=3 ,特征向量为

α3=[111]\alpha_3=\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]

把α1,α2,α3\alpha_1,\alpha_2,\alpha_3竖着排列起来，形成一个矩阵， {α1,α2,α3}\{\alpha_1,\alpha_2,\alpha_3\} 容易看到这是一个正交集（这就相当于我们在三维空间里找到了3个两两互相垂直的坐标轴，但还不是单位坐标轴）。

如果他是单位矩阵，可以有更多性质,现在对α1,α2,α3\alpha_1,\alpha_2,\alpha_3进行单位化，得到单位特征向量.

u1=[−1/21/20],u2=[−1/6−1/62/6],u3=[1/31/31/3]P=[−1/2−1/61/31/2−1/61/302/61/3],D=[800060003]\begin{gathered} u _1=\left[\begin{array}{c} -1 / \sqrt{2} \\ 1 / \sqrt{2} \\ 0 \end{array}\right], \quad u _2=\left[\begin{array}{c} -1 / \sqrt{6} \\ -1 / \sqrt{6} \\ 2 / \sqrt{6} \end{array}\right], \quad u _3=\left[\begin{array}{l} 1 / \sqrt{3} \\ 1 / \sqrt{3} \\ 1 / \sqrt{3} \end{array}\right] \\ P=\left[\begin{array}{ccc} -1 / \sqrt{2} & -1 / \sqrt{6} & 1 / \sqrt{3} \\ 1 / \sqrt{2} & -1 / \sqrt{6} & 1 / \sqrt{3} \\ 0 & 2 / \sqrt{6} & 1 / \sqrt{3} \end{array}\right], \quad D=\left[\begin{array}{lll} 8 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 3 \end{array}\right] \end{gathered}

那么有 A=PDP−1A=P D P^{-1}, 和平常一样. 由于 PP 是方阵且有正交列, 所以, PP 是一个正交矩阵, 而 P−1P^{-1} 就是 P⊤P^{\top}

定理2

如果 AA 是对称矩阵, 那么不同特征空间的任意两个特征向量是正交的. 证 设 v1v_1 和 v2v_2 是对应不同特征值 λ1,λ2\lambda_1, \lambda_2 的特征向量. 为证明 ν1⋅v2=0\nu_1 \cdot v_2=0, 计算

λ1v1⋅v2=(λ1v1)Tv2=(Av1)T⋅v2=(v1⊤A⊤)v2=v1⊤(Av2)=v1T(λ2v2)=λ2v1⊤v2=λ2v1⋅v2\begin{aligned} \lambda_1 v _1 \cdot v _2 & =\left(\lambda_1 v _1\right)^{T} v _2=\left(A v _1\right)^{T} \cdot v _2 \\ & =\left( v _1^{\top} A^{\top}\right) v _2= v _1^{\top}\left(A v _2\right) \\ & = v _1^{T}\left(\lambda_2 v _2\right) \\ & =\lambda_2 v _1^{\top} v _2=\lambda_2 v _1 \cdot v _2 \end{aligned}

因此 (λ1−λ2)v1⋅v2=0\left(\lambda_1-\lambda_2\right) v _1 \cdot v _2=0, 但是 λ1≠λ2\lambda_1 \neq \lambda_2, 所以 v1⋅v2=0v _1 \cdot v _2=0.

通过定理1和定理2我们得到如下一个重要结论：

实对称矩阵的特征值都是实数，而且不同特征值对应的特征向量相互正交。这一点很重要，因为普通矩阵对角化不一定能找到正交矩阵，但实对称矩阵可以，这是一个关键点。

例 将 A=[3−24−262423]A=\left[\begin{array}{rrr}3 & -2 & 4 \\ -2 & 6 & 2 \\ 4 & 2 & 3\end{array}\right] 正交对角化, 其特征方程为

0=−λ3+12λ2−21λ−98=−(λ−7)2(λ+2)0=-\lambda^3+12 \lambda^2-21 \lambda-98=-(\lambda-7)^2(\lambda+2)

解 通过计算可得特征空间的基：

λ=7:v1=[101],v2=[−1/210],λ=−2:v3=[−1−1/21]\lambda=7: v_1=\left[\begin{array}{l} 1 \\ 0 \\ 1 \end{array}\right], v_2=\left[\begin{array}{c} -1 / 2 \\ 1 \\ 0 \end{array}\right], \lambda=-2: v_3=\left[\begin{array}{c} -1 \\ -1 / 2 \\ 1 \end{array}\right]

因为v1,v2v_1,v_2 对应特征值是7，而v3v_3 对应特征值是2，他们是不同的，所以v1,v2v_1,v_2 分别与v3v_3 正交，但是v1,v2v_1,v_2并不正交。 如果我们要在三维空间找到3个两两互相垂直的向量，就需要使用 施密特正交化 ，容易找到 v2v _2 在 v1v _1 上的正交投影是 v2⋅v1v1⋅v1⋅v1\frac{ v _2 \cdot v _1}{ v _1 \cdot v _1} \cdot v _1,与 v1v_1 正交的关于 v2v_2 的分量是:

z2=v2−v2⋅v1v1⋅v1v1=[−1/210]−−1/22[101]=[−1/411/4]z_2= v _2-\frac{ v _2 \cdot v _1}{ v _1 \cdot v _1} v _1=\left[\begin{array}{c} -1 / 2 \\ 1 \\ 0 \end{array}\right]-\frac{-1 / 2}{2}\left[\begin{array}{l} 1 \\ 0 \\ 1 \end{array}\right]=\left[\begin{array}{c} -1 / 4 \\ 1 \\ 1 / 4 \end{array}\right]

于是 {v1,z2}\left\{v_1, z_2\right\} 是关于 λ=7\lambda=7 的特征空间的正交集. 将 v1v_1 和 v2v_2 规范化，我们得到关于 λ=7\lambda=7 特征子空间的单位正交基.

u1=[1/201/2],u2=[−1/184/181/18]u _1=\left[\begin{array}{c} 1 / \sqrt{2} \\ 0 \\ 1 / \sqrt{2} \end{array}\right], u _2=\left[\begin{array}{c} -1 / \sqrt{18} \\ 4 / \sqrt{18} \\ 1 / \sqrt{18} \end{array}\right]

关于 λ=2\lambda=2 对应的特征空间的单位正交基是

u3=1∥2v3∥⋅2v3=13[−2−12]=[−2/3−1/32/3]u_3=\frac{1}{\left\|2 v_3\right\|} \cdot 2 v_3=\frac{1}{3}\left[\begin{array}{r} -2 \\ -1 \\ 2 \end{array}\right]=\left[\begin{array}{r} -2 / 3 \\ -1 / 3 \\ 2 / 3 \end{array}\right]

由定理2, u3u _3 与其他特征向量 u1u _1 和 u2u _2 正交, 因此 {u1,u2,u3}\left\{ u _1, u _2, u _3\right\} 是一个单位正交基. 令

P=[u1u2u3]=[1/2−1/18−2/304/18−1/31/21/182/3],D=[70007000−2]P=\left[\begin{array}{lll} u _1 & u _2 & u _3 \end{array}\right]=\left[\begin{array}{ccc} 1 / \sqrt{2} & -1 / \sqrt{18} & -2 / 3 \\ 0 & 4 / \sqrt{18} & -1 / 3 \\ 1 / \sqrt{2} & 1 / \sqrt{18} & 2 / 3 \end{array}\right], D=\left[\begin{array}{rrr} 7 & 0 & 0 \\ 0 & 7 & 0 \\ 0 & 0 & -2 \end{array}\right]

那么 PP 将 AA 正交对角化且 A=PDP−1A=P D P^{-1}.

二次型的线性替换

例 令 Q(x)=x12−8x1x2−5x22Q( x )=x_1^2-8 x_1 x_2-5 x_2^2, 计算 Q(x)Q( x ) 在 x=[−31],[2−2]x =\left[\begin{array}{r}-3 \\ 1\end{array}\right],\left[\begin{array}{r}2 \\ -2\end{array}\right] 和 [1−3]\left[\begin{array}{r}1 \\ -3\end{array}\right] 处的值. 解

Q(−3,1)=(−3)2−8(−3)(1)−5(1)2=28Q(2,−2)=(2)2−8(2)(−2)−5(−2)2=16Q(1,−3)=(1)2−8(1)(−3)−5(−3)2=−20\begin{aligned} & Q(-3,1)=(-3)^2-8(-3)(1)-5(1)^2=28 \\ & Q(2,-2)=(2)^2-8(2)(-2)-5(-2)^2=16 \\ & Q(1,-3)=(1)^2-8(1)(-3)-5(-3)^2=-20 \end{aligned}

例 求一个变量代换将上例中的二次型变为一个没有交叉项的二次型. 解：上例中二次型对应的矩阵是

A=[1−4−4−5]A=\left[\begin{array}{rr} 1 & -4 \\ -4 & -5 \end{array}\right]

第一步是将矩阵 AA 正交对角化, AA 的特征值是 λ=3\lambda=3 和 λ=−7\lambda=-7, 相应的单位特征向量是:

λ=3:[2/5−1/5];λ=−7:[1/52/5]\lambda=3:\left[\begin{array}{r} 2 / \sqrt{5} \\ -1 / \sqrt{5} \end{array}\right] ; \quad \lambda=-7:\left[\begin{array}{l} 1 / \sqrt{5} \\ 2 / \sqrt{5} \end{array}\right]

这些特征向量自动正交（因为它们属于不同的特征值）且构成 R2R ^2 的一个单位正交基. 取

P=[2/51/5−1/52/5],D=[300−7]P=\left[\begin{array}{rr} 2 / \sqrt{5} & 1 / \sqrt{5} \\ -1 / \sqrt{5} & 2 / \sqrt{5} \end{array}\right], \quad D=\left[\begin{array}{rr} 3 & 0 \\ 0 & -7 \end{array}\right]

那么 A=PDP−1A=P D P^{-1}, 且 D=P−1AP=P⊤APD=P^{-1} A P=P^{\top} A P, 像前面指出的那样, 一个适当的变换是

x=Py, 此处 x=[x1x2],y=[y1y2]x =P y , \text { 此处 } x =\left[\begin{array}{l} x_1 \\ x_2 \end{array}\right], \quad y =\left[\begin{array}{l} y_1 \\ y_2 \end{array}\right]

那么

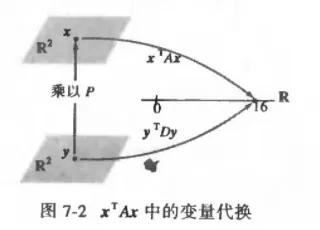
x12−8x1x2−5x22=x⊤Ax=(Py)⊤A(Py)=y⊤P⊤APy=y⊤Dy=3y12−7y22\begin{aligned} x_1^2-8 x_1 x_2-5 x_2^2 & = x ^{\top} A x \\ & =(P y )^{\top} A(P y) \\ & = y ^{\top} P ^{\top} A P y = y ^{\top} D y \\ & =3 y_1^2-7 y_2^2 \end{aligned}

为了说明本例中二次型相等的意义, 我们可以利用新二次型计算 Q(x)Q( x ) 在 x=(2,−2)x =(2,-2) 处的值,首先, 由于 x=Pyx =P y, 我们得到

y=P−1x=P⊤xy=P^{-1} x=P^{\top} x

则有

y=[2/5−1/51/52/5][2−2]=[6/5−2/5]y =\left[\begin{array}{cc} 2 / \sqrt{5} & -1 / \sqrt{5} \\ 1 / \sqrt{5} & 2 / \sqrt{5} \end{array}\right]\left[\begin{array}{r} 2 \\ -2 \end{array}\right]=\left[\begin{array}{r} 6 / \sqrt{5} \\ -2 / \sqrt{5} \end{array}\right]

因此

3y12−7y22=3(6/5)2−7(−2/5)2=3(36/5)−7(4/5)=80/5=16\begin{aligned} 3 y_1^2-7 y_2^2 & =3(6 / \sqrt{5})^2-7(-2 / \sqrt{5})^2=3(36 / 5)-7(4 / 5) \\ & =80 / 5=16 \end{aligned}

这就是例 3 中 Q(x)Q(x) 在 x=(2,−2)x=(2,-2) 处的值, 见图 7-2. 图片

前の章17._用正交阵将实对称矩阵A化为对角阵的步骤
次の章19._本章思维导图