7._近世代数对数学的整体思考 - 线性代数

近世代数对数学的整体思考

参考下图:一个个数字或者物体被称作元素，元素放在一起组成了集合(这个高中就学过)，集合元素支持二元运算则组成了空间，如果空间满足八大性质(加法、数乘、交换律、结合律、单位元等)则被定义为线性空间。空间里元素的距离称为度量空间。我们需要一个尺子作为度量的基准，这个尺子被称为范数，含有范数的空间称为线性赋范空间，如果数据之间没有间隙(也就是数据具备完备性）称为巴拿赫空间。

另一方面，如果在线性空间基础上定义了内积（长度和角度）则称为内积空间。内积空间完备后后是希尔伯特空间，希尔伯特空间在实数域并且是有限维度的则称呼为欧几里得空间。

在整个代数空间里，还可以往另外两个方向抽象：（1）我们默认处理的数都是实数，如果把数从实数延伸到复数，就成了复数空间，简称酉空间，如果里面的数据以面积为主，则称作辛空间

（2）在上面的处理中，要测量向量需要一把“尺子”，我们把所有可能的尺子组成的空间称作对偶空间。对偶空间中的零向量是零泛函，它将每个向量 v 都映射到标量 0，对偶空间是主要用于张量分析里，例如在量子力学里，量子的动量同时受到p和v测量的影响。

详细的空间体系大致如下:

$图片$

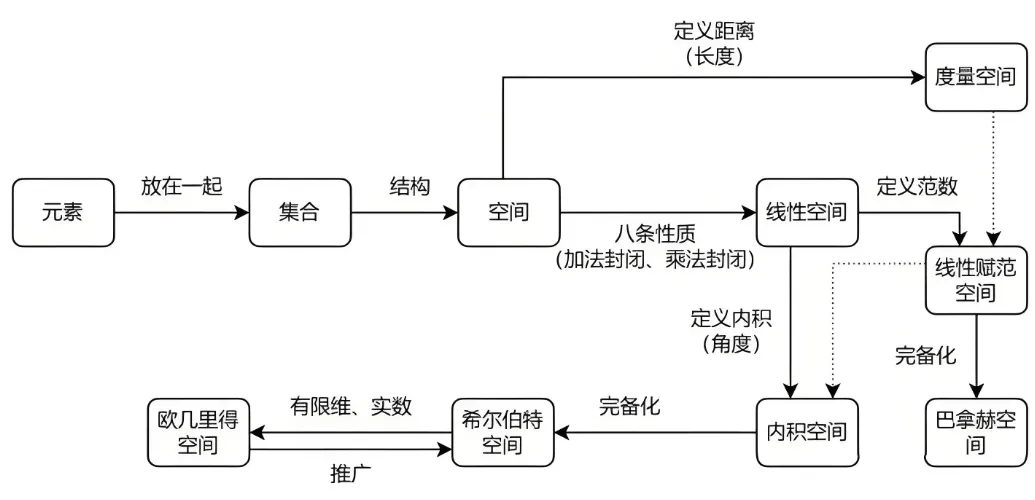
在线性空间里，要特别强调一下数的封闭性，如果集合 $V$ 里的数进行加减乘除仍在 $V$ 里，则 $V$ 称为封闭数域，比如“全体有理数”就是一个封闭数域，因为任何有理数的加减乘除仍在有理数里，但是“全体整数”就不是封闭数域，因为两个数相除有可能是分数。

在代数空间定义了向量之间的运算，如下表，包括了：空间的距离、加法、数乘、内积、领域等。

$图片$

一、空间

把多个元素放在一起就构成了集合，如 $\left\{x_1, x_2, \ldots, x_n\right\}$ 。但是集合是松散，我们还需要定义各个元素之间的"关系"或者说"结构"，加上这层"关系"和"结构"之后，就构成了一个空间

二、线性空间(向量空间)

在空间里，定义一个操作，如果操作满足下面八条性质，则称作线性空间或者向量空间。

$图片$

当然上面八条性质核心是加法和数乘，因此也有人说是两大性质，其余六条性质都可以推到出来。但是，使用八大性质更容易推理。

三、度量空间

如果想把集合中任意的两个元素建立"关系"，首先想到的可能就是去描述它们之间的"距离"。定义了距离的空间称为度量空间。距离的定义应该满足以下四点:

非负性: $d(x, y) \geq 0$
非退化性: $d(x, y)=0 \Leftrightarrow x=y$
对称性: $d(x, y)=d(y, x)$
三角不等式+: $d(x, y)+d(y, z) \geq d(x, z)$

因为定义了距离，因此在度量空间中有了长度的概念。

四、线性赋范空间

定义了范数的线性空间称为线性赋范空间。范数的定义应该满足以下四点:

非负性: $\|x\| \geq 0$
非退化性： $\|x\|=0 \Leftrightarrow x=0$ -齐次性+: $|a x \|=| a|\cdot||x| \mid$
三角不等式： $\|x+y\| \leq\|x\|+\|y\|$ 范数可以理解为空间中一个元素到零元的距离。因此，我们很容易根据范数的定义诱导出距离的定，如 $d(x, y)=\|x-y\|$ 。因此通常我们认为赋范空间也是一种度量空间。

值得注意的是，在范数的定义过程中，非退化性要求该空间内一定有一个零元，齐次性要求对乘法封闭，三角不等式要求对加法封闭。因此，范数必须定义在线性空间内，一个赋范空间一定是线性的，称为线性赋范空间。

五、内积空间

定义了内积的线性空间称为内积空间。内积的定义应该满足以下四点:

非负性: $\langle x, x\rangle \geq 0$
非退化性： $\langle x, x\rangle=0 \Leftrightarrow x=0$
共轭对称性 : $\langle x, y\rangle=\overline{\langle y, x\rangle}$
第一变元线性: $\langle a x+b y, z\rangle=a\langle x, z\rangle+b\langle y, z\rangle$
第二变元共轭线性: $\langle z, a x+b y\rangle=\bar{a}\langle z, x\rangle+\bar{b}\langle z, y\rangle$

关于距离、范数和内积的总结如下图

$图片$

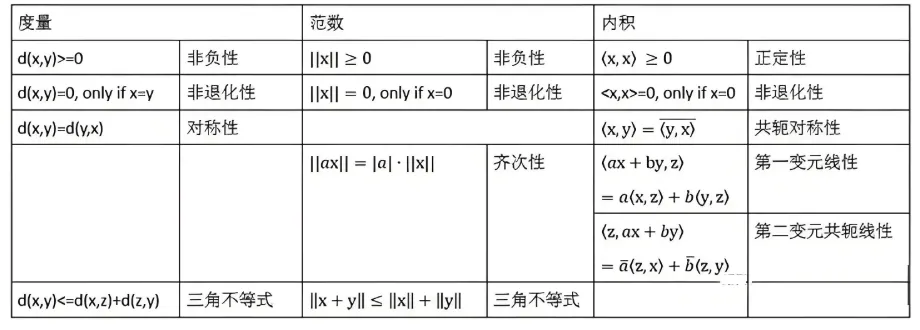
事实上，定义了内积以后也很容易诱导出范数的定义，如 $\|x\|=\sqrt{\langle x, x\rangle}$ 。因此，通常我们认为内积空间也是一种赋范空间，同时也是一种度量空间。

定义了内积和范数，就可以定义线性空间中两个向量的夹角，即 angle $(x, y)=\frac{\langle x, y\rangle}{\|x\| \cdot\|y\|}$ 。因此，在内积空间中，我们有了长度和角度的概念。

下面的例题对上面进行了简单的解释。详见向量单位化

例 已知三维空间里有2个向量，我们可以求出其中的部分数据。

\boldsymbol{x}=\left(\begin{array}{l}-1 \\ 2 \\ 3\end{array}\right), \boldsymbol{y}=\left(\begin{array}{l} 1 \\ 0 \\ 3 \end{array}\right)

$图片$

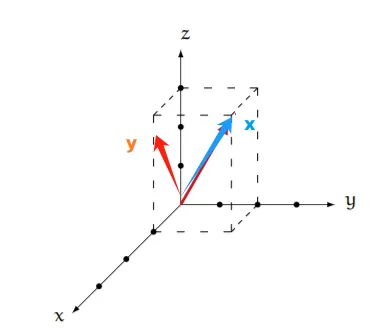
解： ①求向量的长度。 $||x||$ = $\sqrt{(-1)^2+2^2+3^2}=\sqrt{14}$ $||y||$ = $\sqrt{(1)^2+0^2+3^2}=\sqrt{10}$

② 求2个向量的夹角 $[[x,y]=-1*1+2*0+3*3=8$ 所以夹角 $\theta=\arccos \frac{8}{14*10}=\arccos \frac{2}{35}$

③ 求测量向量的尺子。可以有多个尺子

\vec{e}= \frac{x}{||x||}= \left(\begin{array}{l}-1/\sqrt{14} \\ 2/\sqrt{14} \\ 3/\sqrt{14} \end{array}\right)

或

\vec{e}= \frac{x}{||x||}= \left(\begin{array}{l}1/\sqrt{10} \\ 0/\sqrt{10} \\ 3/\sqrt{10} \end{array}\right)

六、希尔伯特空间和完备性

希尔伯特空间，即完备的内积空间。那么什么是完备性 (completeness) 呢? 这里需要介绍一下收敛列和柯西列

收敛列: 设 $(X, d)$ 为度量空间， $\left\{x_n\right\}$ 为 $X$ 中的数列，若存在 $x \in X$ 使得 $\lim _{n \rightarrow \infty} d\left(x_n, x\right)=0$ ，则 $\left\{x_n\right\}$ 在 $X$ 中收敛， $\left\{x_n\right\}$ 称为收敛列， $x$ 称为 $\left\{x_n\right\}$ 的极限。

简而言之，如果一个度量空间中的数列存在极限，且这个极限也在这个空间内，那么这个数列就是一个收敛列。举例，如 $X=(0,1)$ ，那么数列 $\left\{x_n \left\lvert\, x_n=\frac{1}{n}\right.\right\}$ 就不是一个空间 $X$ 的收敛列，因为它的极限 0 不在空间 $X$ 内。

柯西列：设 $(X, d)$ 为度量空间， $\left\{x_n\right\}$ 为 $X$ 中的数列， $\forall \epsilon>0, \exists N \geq 1$ , s.t. $\forall m, n \geq N, d\left(x_m, x_n\right)<\epsilon$ ，则称它为柯西列。把一个数列从大到小排列，如果前一项减去后一项的差越来越小并最终趋近于零，那么这个数列就是一个柯西列。收敛列一定是一个柯西列，但是柯西列不一定是一个收敛列。如在 $X=(0,1)$ 空间中的数列 $\left\{x_n \left\lvert\, x_n=\frac{1}{n}\right.\right\}$ ，它是一个柯西列，但不是一个收敛列。

完备性：设 $(X, d)$ 为度量空间，如果 $X$ 中的任意柯西列都是收敛列，则 $(X, d)$ 为完备度量空间。

因此，一个完备的度量空间一定是一个闭集。

近似代数对运算的整体思考-群、环、域、格

下面介绍一下数学界对“代数运算”的整体思考，代数，在初中时就学过，比如加法、减法、乘法、除法、乘法、开方等。我们有没有想过，这些“法则”是怎么定义的？或者说，这种“法则”的产生是一种巧合还是一种人类数学史发展的必然？如果是人类的定义，比如定义乘法 $ab=ba$ ，当把 $a,b$ 扩展到矩阵时，又发现 $AB \ne BA$ ，因此，我们需要捋顺一下整个代数定义的基本思路。参考下图

代数的运算核心是：群。我们对运算需要发散思维，比如加法，传统的加法需要是数字，比如 $1+2=3$ ，如果我们问：“abc+def=?” 我们能否得到结果是"abcedf"呢？具体参考下图

首先在集合里，定义一个二元运算，二元运行的结果仍在集合里，含有这种性质的集合被称作原群。如果原群支持结合率则是半群。如果半群有单位元则是幺半群，如果幺版群支持逆元则是群，如果群支持交换律则是阿贝尔群。

上面的结果如下表所示

$图片$

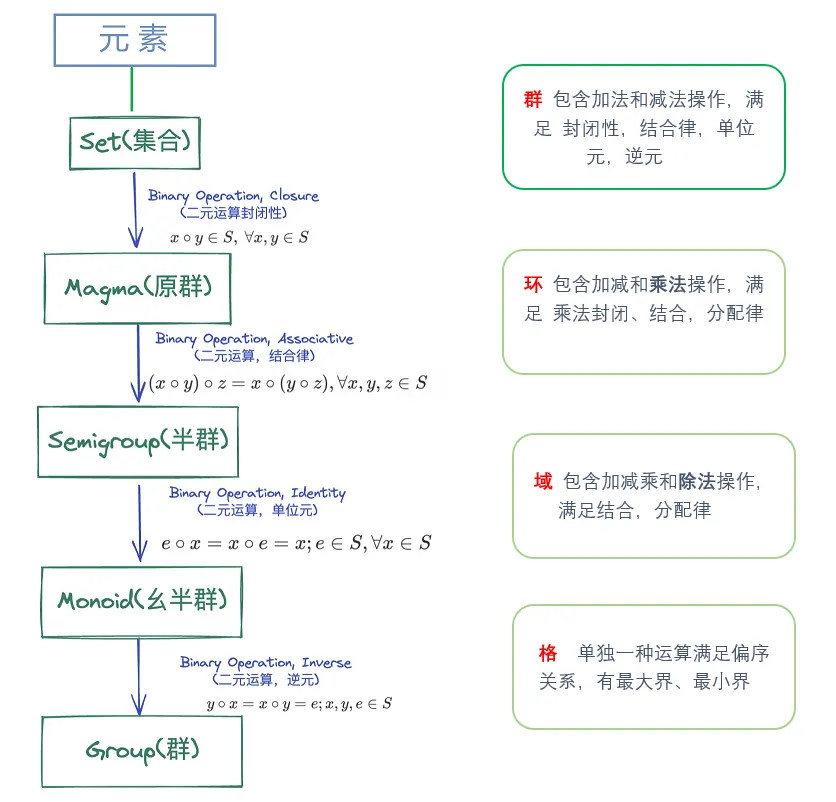
元素

我们把一个个“物体”称作元素。他可以是实体也可以是虚拟的，比如班级里的男生，那么男生就是一个“元素”。元素放在一起就组成了集合Set

集合

这是集合论的创立者康托尔对集合的定义，物以类聚为集合。比如班里的男生集合，班里的女生集合。

这是一个直观且朴素的定义，比较容易理解，但是不够严格。比如著名的罗素悖论(Russell's paradox)就对康托尔的集合论造成了致命一击，甚至引发了第三次数学危机。

康托尔对于集合的研究被称为朴素集合论。而为了规避罗素悖论，数学家们对集合论进行了严格公理化，被称为公理化集合论。

集合论可以说是现代数学的基石，几乎所有分支里面都会集合的概念。

比如集合加上结构，构成了空间，再进一步衍生出拓扑空间，度量空间，线性空间等，这是线性代数的分支。如下图

集合的特性 集合要满足以下三个特性：无序性。{1,2,3}与{3,2,1}是一样的。互异性。集合内的元素都是不同的。确定性。一个元素属不属于一个集合是确定的，不能含糊。高富帅不是集合，因为定义模糊。但是身高1米八、年薪100w的人是集合，因为是确定的

集合元素之间的二元运算则称作原群

原群 Magma

二元运算，通俗一点说，二元运算就是：以两个元素为输入，经过一个运算后得到一个元素，如下图所示 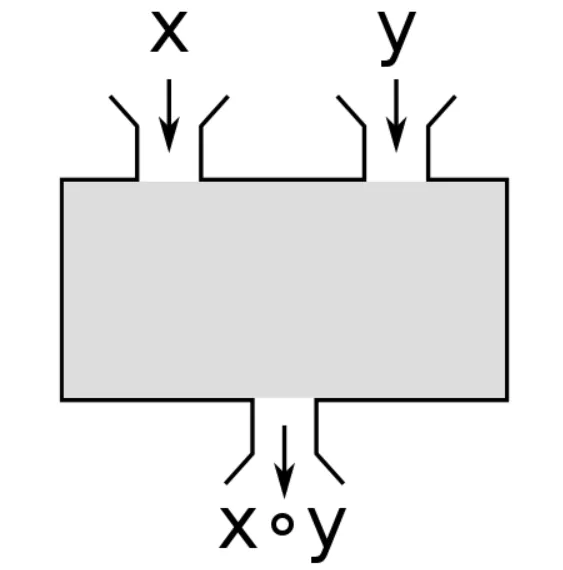$图片$ {width=300px}

二元运算可以随意定义：比如集合中两个元素为 x 和 y ，我们可以将运算定义为：

加法： $x+y$
乘法： $x \times y$
自定义的运算： $(x+y) / 2 \pi$

又比如集合为 $\{剪刀，石头，布 \}$ 我们定义运算的结果为：剪刀石头布三者，打架后谁赢了，如下图所示：

$图片$

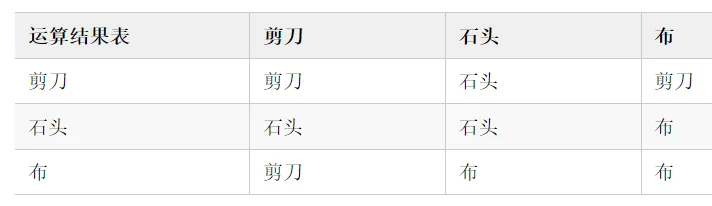
Magma 原群

如果二元运算的结果还在集合中，我们称这个集合在该运算下闭合（Closed），这一性质叫做封闭性（Closure）。

集合与在该集合上的一个二元封闭性运算，构成了原群（Magma）。注意这里面有三个关键词：集合，二元运算，封闭性。

半群

结合律（Associative property）结合律依然是描述二元运算的，通俗一点讲，就是集合中多个元素在二元运算上的结果与结合顺序没有关系。

比如二元运算为 $\circ$ ，集合为 $S$ ，则 $x \circ(y \circ z)=(x \circ y) \circ z, \forall x, y, z \in S$ ，如下图所示：

$图片$

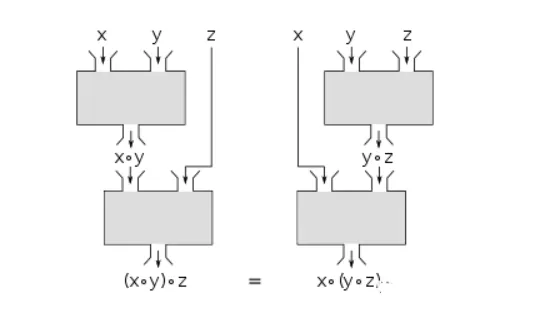
半群(Semigroup)

如果我们在原群的基础上，再加一点约束条件：结合律，则原群(Magma)变成一个半群(Semigroup)。

幺半群(Monoid)

假设有一集合S，e为集合中的元素，如果对于 $S$ 中任意元素 $a$ ，有一运算 o ：

如果满足： $e \circ a=a$ ，则称 e 为左单位元
如果满足： $a \circ e=a$ ，则称 e 为右单位元
如果满足： $e \circ a=a \circ e=a$ ，则称 e 为单位元

幺半群就是包含单位元的半群。

群(Group)

假设集合 $S$ 的单位元为 $e$ ，对于集合中的元素 x ，

如果集合中存在元素 y 和运算 $\circ$ 使得 $x \circ y=e$ ，则称 y 为 x 的右逆元
如果集合中存在元素 y 和运算 0 使得 $y \circ x=e$ ，则称 y 为 x 的左逆元
如果集合中存在元素 y 和运算 $\circ$ 使得 $x \circ y=y \circ x=e$ ，则称 y 为 x 的逆元

比如实数的加法逆元为 -x ，非零实数的乘法逆元为 $1 / x$

如果我们在么半群Monoid 的基础上，再加一点约束条件：其中任意元素都存在逆元，则么半群（Monoid）变成一个群（Group）。

到了群这一级别，还可以继续定义，比如运算满足交换律的群被称为阿贝尔群，如果满足元素到自身的映射称作置换群，另外还有对称性、有限群等等

环、模、格、是什么意思

理解了上面的定义后，再理解模、格、环就容易了

环（Ring）

环是一个集合 $R$ ，定义了两种运算：加法（+）和乘法（·），满足以下条件： • 加法构成交换群（阿贝尔群），即： ◦ 封闭性、结合律、存在零元 $0$ 、每个元素有负元。 ◦ 加法交换律： $a + b = b + a$ 。 • 乘法满足结合律： $(a \cdot b) \cdot c = a \cdot (b \cdot c)$ 。 • 分配律：乘法对加法满足左分配律 $a \cdot (b + c) = a \cdot b + a \cdot c$ 和右分配律 $(a + b) \cdot c = a \cdot c + b \cdot c$ 。

模（Module）

模是环上的推广，类似于向量空间，但标量来自环而非域。具体地： • 设 $R$ 为环， $M$ 是一个加法交换群。 • 定义标量乘法 $R \times M \to M$ ，满足： ◦ 分配律： $r \cdot (m + n) = r \cdot m + r \cdot n$ ， $(r + s) \cdot m = r \cdot m + s \cdot m$ 。 ◦ 结合律： $(r \cdot s) \cdot m = r \cdot (s \cdot m)$ （若环含幺元，则还需满足 $1 \cdot m = m$ ）。

格（Lattice）

格是一个偏序集 $(L, \leq)$ ，其中任意两个元素 $a, b$ 都有： • 最小上界（并，join）： $a \vee b$ 。 • 最大下界（交，meet）： $a \wedge b$ 。

群、模、格、环的关系可以用下表简单比较

四者的区别

结构	核心运算	关键性质	典型应用
群	单一运算（如加法）	封闭性、结合律、逆元、单位元	对称性研究（如晶体结构、密码学）
环	加法和乘法	分配律、乘法结合律	数论（整数环）、代数几何
模	标量乘法和加法	依赖环结构，推广向量空间	表示论、同调代数
格	并、交（序关系）	偏序下的上下确界存在性	逻辑电路设计、数据库查询优化

代数结构的层次性群 → 环 → 模：逐步增加运算复杂度。格独立于运算，但可与环/群结合（如分配格）。

数的封闭性

为什么特别强调封闭性？因为这和“群论”有关，在研究五次方程时，数学家得出了五次方程没有求根公式。这里涉及到数据的封闭性，比如一次方程 $ax=b$ 在有理数范围 $Q$ 内可以得到求根公式 $x=\dfrac{b}{a}$ ，而加减乘除不会让有理数变成无理数所以他是封闭的。再看二次方程，比如 $x^2=2$ 此时 $x=\pm \sqrt{2}$ ,因为 $\sqrt{2}$ 是无理数，此时就不能说方程在有理数访问内有解，我们需要扩展数域，即把有理数Q扩展为实数R，这样方程就有了解。再如 $x^2=-1$ 可以发现，在实数R里，也无法满足方程的解，我们再把实数扩展为虚数C,这样方程就得到 $a+bi$ ，再往上还能扩展吗？

数从 自然数-整数-有理数-实数-复数 一步步扩展，到了复数 $a+bi$ 这里似乎就扩展完了。那我们能否定义比复数更大的数域，例如“超复数”，还真有数学家这么做了，复数 $a+bi$ 看起来是由2个数字组成，如果是超复数应该是由3个数字组成，即 $a+bi+cj$ , 英国数学家哈密顿最先提出了三元数，三元数应该满足2个基本条件 ①三元数，具有加减法、数乘运算的数。 ②三元数应当可在三维空间表示，但仍未发现其存在。但是，经过了几次的证明后，最后证明三元数无法存在。但是哈密顿给出了四元数。

四元数，是简单的超复数。复数是由实数加上虚数单位 $i$ 组成，其中 $i ^2=-1$ ，即 $a i+b j+c k+d$ 。相似地，四元数都是由实数加上三个虚数单位 $i$ ， $j$ 和 $k$ 组成，而且它们有如下的关系： $i^2=j^2=k^2=-1, ~ i^0=j^0=k^0=1$ ，每个四元数都是 $1, ~ i, ~ j$ 和 $k$ 的线性组合，即是四元数一般可表示为 $a+b i+c j+d k$ ，其中 $a, ~ b, ~ c, ~ d$ 是实数。 $X$ 轴与 $Z$ 轴相交平面中 $X$ 轴正向向 $Z$ 轴正向的旋转， $k$ 旋转代表 $Y$ 轴与 $X$ 轴相交平面中 $Y$ 轴正向向 $X$ 轴正向的旋转， $-i, ~-j, ~ k$ 分别代表 i，j，k旋转的反向旋转。明确地说，四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话，四元数就代表着一个四维空间，相对于复数为二维空间。但是四元数具有很大的不稳定性 例如四元数的 $n$ 阶多项式能有多于 $n$ 个不同的根

总之，可以说，数的定义复数这里就结束了，再往上扩展，不管是几何意义还是实用性已经不大。所以，超复数一说基本上是昙花一现

欧氏空间与非欧空间

如果仔细观看上面图片，最终结果是欧氏空间，初中，我们都学过勾股定理，也都学过三角形内角和为 $180$ 度这个结论，这里就不得不提欧式几何，由欧几里得创立的几何学被称为欧氏几何。。

欧几里得（Euclid，约公元前325年—公元前265年）是古希腊数学家，以其所著的《几何原本》（简称《原本》）闻名于世。曾受业于柏拉图学园。后应埃及托勒密国王邀请，从雅典移居亚历山大，从事数学教学和研究工作。他一生治学严谨。所著《几何原本》共13卷，是世界上最早公理化的数学著作，影响着历代科学文化的发展和科技人才的培养。

$图片$ {width=200px}

欧几里得通过5条公理和5条公设并基于点线面公设推导出整个的二维平面和三维空间中的几何，因此，欧几里得几何也被称为“欧氏几何”。

欧几里得给出的几何定义源自五条公理也叫做公设：所谓公理就是“大家公认的道理，不需要证明的”

五大公社： 1.过两点能作且只能作一直线； 2.线段(有限直线)可以无限地延长； 3.以任一点为圆心,任意长为半径,可作一圆； 4.凡是直角都相等； 5.同平面内一条直线和另外两条直线相交，若在直线同侧的两个内角之和小于180°，则这两条直线经无限延长后在这一侧一定相交。

这些断言除了「公理5」外，都是显而易见的。由第五条公社退出了三角形内角和为180度。

《几何原本》第五公设与非欧几何

长期以来，数学家们对前面四条公理没有意义，但是对第五条公式并不是很满意。第五公设和前四个公设比较起来，显得文字叙述冗长，而且也不那么显而易见。有些数学家还注意到欧几里得在《几何原本》一书中直到第29个命题中才用到，而且以后再也没有使用。也就是说，在《几何原本》中可以不依靠第五公设而推出前28个命题。因此，一些数学家提出，第五公设能不能不作为公设，而作为定理？能不能依靠前四个公设来证明第五公设？这就是几何发展史上最著名的，争论了长达两千多年的关于“平行线理论”的讨论。由于证明第五公设的问题始终得不到解决，人们逐渐怀疑证明的路子走的对不对？第五公设到底能不能证明？并由此产生了罗氏几何，黎曼几何等。

$图片$

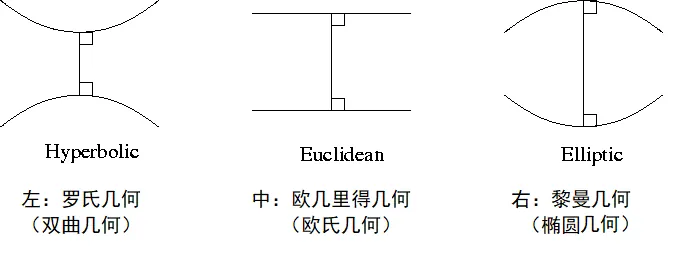
下图显示了三种几何观点中，三角形内角和的不同。即：如果不接受欧几里得第五条公社，那么，三角形内角和可以小于180度，也可以大于180度。详见欧几里得介绍，据说，正式根据非欧几何的观点，爱因斯旦才得出了时空弯曲的概念。

$图片$

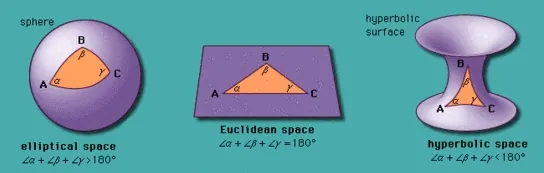
延伸阅读：关于距离

根据欧氏几何，可以得到平面上两点之间的距离为： $d=\sqrt{(x_2-x_1)^2 + (y_2 -y_1)^2}$ ，参考下图，可以看到两点之间的距离，为直角三角形斜边的长度。整个《高等数学》研究微积分本质都是“以直带曲”，使用的都是欧氏几何，所以我们在“拟合”曲线时，只能使用三角形的斜边，而不能使用直角边拟合曲线，详见此处。整个数学体系包括线性代数也是采用欧氏几何来定义距离，但是欧氏距离并不是唯一的“数学定义”，其中最有名的是曼哈顿距离

$图片$

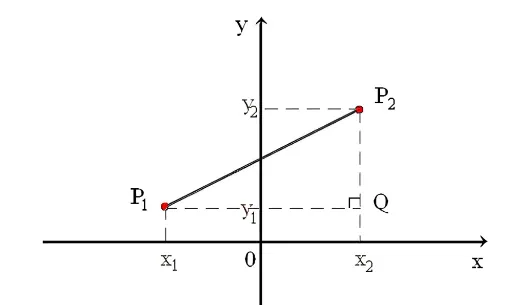
曼哈顿距离

曼哈顿距离得名于曼哈顿市区，曼哈顿市区的道路如棋盘—般横纵交错，那么从一点到另一点的最短路径，只能横向或者纵向移动，因此两点之间最短的距离为： $s=|x|+|y|$ 。

下图展示了两种距离的定义的区别 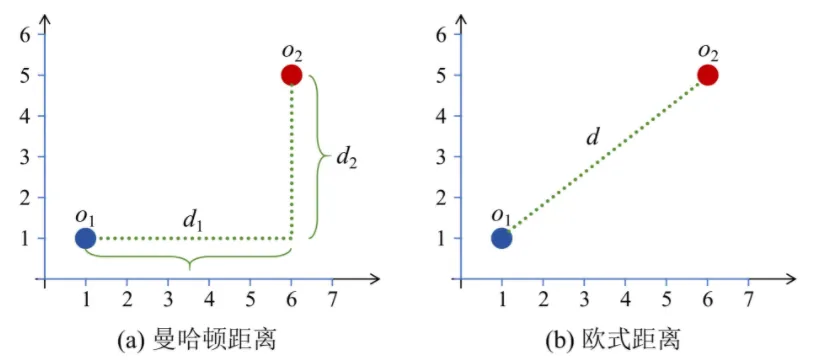$图片$ {width=500px}

在计算机体系里，比如图论路径里，多使用曼哈顿距离。

介绍以上内容，主要是方便读者需要拓展思维，对于一种定义，并不代表“一定是这样定义”的，人们可以给出多种定义，但是只有符合“人类”认知的定义才能被接受下拉。比如牛顿力学和爱因斯坦力学，爱因斯坦提出相对论后，很多人嘲笑牛顿力学已经落后了。但是，爱因斯坦的相对论只有在接近光速才适用，而我们日常生活里，基本上仍以牛顿力学为主，同样的，欧几里得两千多年前提出的“距离”的概念，虽然很“老”，但是他最接近我们生活的实际感受，因此，整个数学体系都是以欧氏几何为主，只有专业的才介绍非欧几何。