1._序言_线性代数用来干什么的 - 线性代数

线性代数用来干什么的

线性代数用来干什么的,说起来很简单，就是解方程。有许多同学感觉，线性代数太难了，或者说太抽象了，这是因为，线性代数的学习方法和高等数学完全不一样，也就是说你学习线性代数首先你得换学习思想，它完全是一套全新的学习思想。更直白点：（1）高等数学（微积分）是先学习一个知识点，然后通过大量做题就能学会。（2）线性代数则相反，必须理解他的概念，至于题目，反而并不是那么重要。比如矩阵初等变换，你会一个三阶行列式后，后面的四阶、五阶、六阶理论上你就都会了，相反，如果你三阶的你不理解其中的概念，你做再多的四阶、五阶、六阶初等变化都没用。

线性代数的本质是解方程，而且我们只研究一次方程和二次方程

一次方程

在初中，我们就会解方程，例如

\left\{\begin{array}{l} x+y=3 \\ x-y=1 \end{array}\right.

这有啥好研究的？这是因为，这是只有2个未知量方程，但是现实生活中可能需要解成百上千个方程，例如预测天气预报，估算导弹飞行路程。

美国学者David C. Lay 在《线性代数及其应用》书就介绍一个小故事：1949 年夏末, 哈佛大学教授列昂惕夫研究美国经济时，他从美国劳动统计局获得了25 万多条信息. 列昂惕夫把美国经济分解为 500 个部门, 例如煤炭工业、汽车工业、交通系统，等等，对每个部门，他写出了一个描述该部门的产出如何分配给其他经济部门的线性方程.最后得到了一个包含 500 个未知数的 500 个方程的方程组,如何解这个方程？理论上是可以解出来的，但是当时确实无法解出来，由此促使数学家来研究解方程。

高斯消元法

在初中就介绍过高斯消元法，高斯消元法的想法很简单：逐渐消去（减少）未知数的个数。例如解下面三元一次方程

\left\{\begin{aligned} x+2 y-z & =1 ...① \\ 4 x+9 y-3 z & =8 ...②\\ -2 x-3 y+7 z & =10 ...③ \end{aligned}\right.

提示：在消元时，我们脑子里一定要记住我们是要干什么的，先消去x，再消去y，就能得到z

第一步：消去方程组中方程②、方程③中的变量 $x$

先保持第一行不变，利用第一行消去第二行、第三行的 $x$ , 而消去的方法也非常简单，第二、第三行 $x$ 的系数是4与-2，我只要用第一行的 $x$ 倍数的相反数加上去就能消掉第二、第三行的 $x$

方程 $①\times(-4)+$ 方程②，方程②变为方程②’ $y+z=4$ 。

方程 $① \times 2+$ 方程③，方程③变为方程③ $y+5 z=12$ ，

此时原方程组变为

\left\{\begin{aligned} x+2 y-z & =1 ...①\\ y+z & =4 ...②'\\ y+5 z & =12 ...③' \end{aligned}\right.

第二步：消去方程③'中的变量 $y$

再看第二步消元，保持第二行不变，利用第二行消去第三行 $y$ ,我们能够想象，假设是四元一次方程组，这第二步应该是利用第二行消去第三行、第四行的 $y$ , 消去的过程也和第一步类似，使用倍数的相反数加上去就能消去

方程 $②' \times(-1)+$ 方程③'，方程③'变为方程④'

$4 z=8$

此时方程组变为阶梯状结构：

\left\{\begin{array}{r} x+2 y-z=1, \\ y+z=4, \\ 4 z=8 . \end{array}\right.

目标达到。第三步：从下往上，逐个求变量的值往回代入，不难得到方程组的唯一解为 $(x, y, z)=(-1,2,2)$ ．

当然，如果我们不急于求解，再从下往上消去可以得到

\left\{\begin{array}{r} x+0 y+0z=-1, \\ y+0z=2, \\ z=2 . \end{array}\right.

矩阵

在上面求解方程组的过程中，我们可以对变量 $x,y,z$ “视而不见”，也就是只有系数会影响结果，而变量的名是叫 $x,y,z$ 还是 $a,b,c$ 对解方程没有影响。因此，如果提取方程的系数,作为一个数表，给他一个名字--矩阵。

\left[\begin{array}{l} &1 & 2 & -1 \\ &4 & 9 & -3 \\ &-2 & -3& 7 \\ \end{array}\right]

如果连同等号右边的值，则叫做--增广矩阵。

\left[\begin{array}{l} &1 & 2 & -1 & 1 \\ &4 & 9 & -3 & 8 \\ &-2 & -3& 7 & 10 \\ \end{array}\right]

当方程组化为阶梯状结构对应的矩阵称作-- 阶梯形矩阵(下面都是0) , 阶梯形矩阵是重点内容，详见阶梯形矩阵

\left[\begin{array}{l} &1 & 2 & -1 & 1 \\ &0 & 1 & 1 & 4 \\ &0 & 0 & 4 & 8 \\ \end{array}\right]

毫无疑问，阶梯形矩阵是非常好的，因为只要从下往上回代，就能立刻得到方程组的解。

如果继续把系数化为1，其它列系数为零，就是--行简化阶梯形矩阵（行最简形矩阵）

\left[\begin{array}{cccc} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 2 \\ \end{array}\right] ...(1)

一个矩阵，左边是单位矩阵 $E$ ，其余元素都是0的矩阵，称作--标准形矩阵 所以，上面矩阵（1）的标准形是

\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{array}\right] ...(1)

如果方程组有解，我们就称方程组是相容的。如果方程组无解则称呼方程组是不相容的。

这里再提2个概念，详见逆矩阵

每个方阵会对应一个行列式，矩阵 $A$ 对应的行列式记做 $det A$ , 如果 $det A=0$ 则矩阵称为奇异矩阵或退化矩阵，如果 $det A \ne 0$ 则矩阵称为非奇异矩阵或非退化矩阵

典型的一次方阵

典型的一次方程形式如下:

\left\{\begin{array}{c} a_{11} x_1+a_{12} x_2+\cdots+a_{1 n} x_n=b_1 \\ \vdots \\ a_{i 1} x_1+\cdots+a_{i i} x_i+\cdots+a_{i n} x_n=b_i \\ \vdots \\ a_{n 1} x_1+a_{n 2} x_2+\cdots+a_{n n} x_n=b_n \end{array}\right.

在《线性代数》这门课里，为了研究解一次方程，引入了行列式，引入了矩阵，进而又引入了伴随矩阵，矩阵的秩，逆矩阵、引入了线性相关与线性无关等概念相关，最终目的都是为了解一次方程。

在附录1：线性方程组、行列式、矩阵、向量组的关系我们从上帝的视角，来一次性概括一次方程要解决的问题。

二次方程

为了研究二次方程（其实是二次多项式），引入了标准型，二次型分为标准二次型和不标准二次型，这两者的区别在哪，就是它们对应的矩阵不一样，这其中有一个问题就是我们要把非标准化成标准，这个时候本质上需要做一件事，就是把矩阵从不对角变成对角，这个时候你为了完成这个任务你就必须准备一套理论，这套理论就是特征值与特征向量这套理论，这条理论我是非常喜欢的，为什么呢，因为它非常的深刻。为了解决二次方程的问题，矩阵产生了三大性质：相似、等价与合同。而为了解决图形变换问题，引入了正交变换，为了方便生成正交矩阵又引入了施密特正交化。

图像扶正

每一个二次型都对应一个图形，而有时候有些图形会歪了，比如下面的斜椭圆

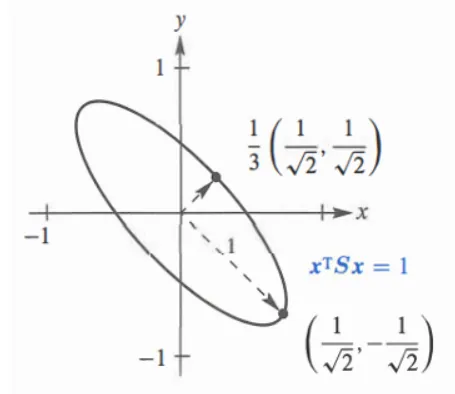$图片$ {width=300px}

我们的想法是把他“扶正”，扶正是口语的说法，其实就是做一个“旋转”

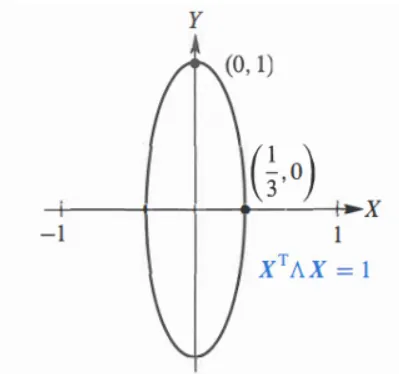$图片$ {width=300px}

在这个旋转过程里，到底是坐标轴旋转还是图像旋转,我们基本上不会深究，因为，我们使用的是对称矩阵，就像太阳绕着地球转还是地球绕着太阳转，核心在于你选择的参照物。通效果上是图形旋转但是从理解上坐标轴旋转容易理解。

要旋转就找找到一个矩阵，因此，这里就产生了如何找到旋转矩阵，旋转的步骤（以3维为例）： ①给任意一个3阶方阵，把每个矩阵看成3个列向量（3维空间）。

②这3个向量当做一个坐标系，我们称呼基，但是此时最大的问题是图像“失真”严重，比如一个圆可能变成了椭圆甚至直线。（详见特征值与特征向量），而且此时的坐标系不一定互相垂直，因此引入施密特正交化来让这3个向量互相垂直。详见施密特正交化

③ 进一步，我们发现如果这个矩阵是对称矩阵就比较好，对称矩阵能让圆保持椭圆甚至圆，而且对称矩阵的坐标系总是互相垂直。

④有了上面的结论我们得到一个理想的旋转矩阵--他是对称矩阵，又是单位矩阵，这样做图形变换最好，变换后的圆仍是圆，椭圆仍是椭圆，此时的矩阵称作正交矩阵，换句话说，正交矩阵保持了几何体原始的形状（更简单的理解是：图像不变，坐标轴旋转）

二次型概述

二次型是变量的二次乘积项的和，类似于 $a x^2+b x y+c y^2$ 的多项式子，一般包括两个变量乘积项和一个变量平方两种形式。二次型是个函数，如上式可以写成 $f(x, y)=a x^2+b x y+c y^2$ 的等式形式。

有人疑惑: 这个多项式不是线性函数啊，这二次型和线性代数有什么关系?

如果我们把函数 $f(x, y)=a x^2+b x y+c y^2$ 的自变量换一下, 把单变量 $x 、 y$ 合成一个变向量那么再引入矩阵，原二元二次函数就可以改写成一元二次向量函数:

f(x)=\left(\begin{array}{ll} x & y \end{array}\right)\left[\begin{array}{cc} a & \frac{b}{2} \\ \frac{b}{2} & c \end{array}\right]\left(\begin{array}{l} x \\ y \end{array}\right)

是不是很熟悉，这就是把二次项转换为了矩阵的运算，上面研究的矩阵的性质和那套理论就可以应用到二次型上。

计算复杂矩阵

利用线性代数，可以计算复杂矩阵，例如

已知矩阵 $\boldsymbol{A}=\left(\begin{array}{ccc}0 & -1 & 1 \\ 2 & -3 & 0 \\ 0 & 0 & 0\end{array}\right)$ . 求 $\boldsymbol{A}^{99}$ .

解: 要求 $A^{99}$ ，不就是求 99 个 $\mathrm{A}$ 相乘吗? 这又不难 (至少理论上是，一个个相乘吧)，现在有计算机了，计算确实不难，但是在没有计算机的年代，要计算99个A相乘，只能说 "看上去很美 "，大概率，你是做不出来的，或者很容易出错的。因此，数学家重要想办法，到底有没有更简便的方法来计算这个矩阵。

解 (I) 计算 $\boldsymbol{A}$ 的特征多项式 $|\lambda \boldsymbol{E}-\boldsymbol{A}|$ .

|\lambda \boldsymbol{E}-\boldsymbol{A}|=\left|\begin{array}{ccc} \lambda & 1 & -1 \\ -2 & \lambda+3 & 0 \\ 0 & 0 & \lambda \end{array}\right| {\text { 按第三行展开 }} \lambda\left(\lambda^2+3 \lambda+2\right)=\lambda(\lambda+1)(\lambda+2) .

因此, $\boldsymbol{A}$ 有 3 个不同的特征值: $-2,-1,0$ . 由于属于不同特征值的特征向量线性无关, 故 $\boldsymbol{A}$ 有 3 个线性无关的特征向量, $\boldsymbol{A}$ 相似于对角矩阵 $\left(\begin{array}{ccc}-2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0\end{array}\right)$ .

分别计算 $\boldsymbol{A}$ 的属于特征值 $-2,-1,0$ 的特征向量. 当 $\lambda=-2$ 时, 解 $(-2 \boldsymbol{E}-\boldsymbol{A}) \boldsymbol{x}=\mathbf{0}$ . 由于

-2 \boldsymbol{E}-\boldsymbol{A}=\left(\begin{array}{ccc} -2 & 1 & -1 \\ -2 & 1 & 0 \\ 0 & 0 & -2 \end{array}\right) \rightarrow\left(\begin{array}{ccc} -2 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right),

故 $(1,2,0)^{\mathrm{T}}$ 为 $\boldsymbol{A}$ 的属于特征值 -2 的一个特征向量. 当 $\lambda=-1$ 时, 解 $(-\boldsymbol{E}-\boldsymbol{A}) \boldsymbol{x}=0$ . 由于

-\boldsymbol{E}-\boldsymbol{A}=\left(\begin{array}{ccc} -1 & 1 & -1 \\ -2 & 2 & 0 \\ 0 & 0 & -1 \end{array}\right) \rightarrow\left(\begin{array}{ccc} -1 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right),

故 $(1,1,0)^{\mathrm{T}}$ 为 $\boldsymbol{A}$ 的属于特征值 -1 的一个特征向量. 当 $\lambda=0$ 时, 解 $(0 \boldsymbol{E}-\boldsymbol{A}) \boldsymbol{x}=\mathbf{0}$ . 由于

0 \boldsymbol{E}-\boldsymbol{A}=\left(\begin{array}{ccc} 0 & 1 & -1 \\ -2 & 3 & 0 \\ 0 & 0 & 0 \end{array}\right)

故 $(3,2,2)^{\mathrm{T}}$ 为 $\boldsymbol{A}$ 的属于特征值 0 的一个特征向量. 令 $\boldsymbol{P}=\left(\begin{array}{lll}1 & 1 & 3 \\ 2 & 1 & 2 \\ 0 & 0 & 2\end{array}\right)$ , 则 $\boldsymbol{P}^{-1} \boldsymbol{A} \boldsymbol{P}=\left(\begin{array}{ccc}-2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0\end{array}\right)$ . 计算 $P^{-1}$ 得, $P^{-1}=\left(\begin{array}{ccc}-1 & 1 & \frac{1}{2} \\ 2 & -1 & -2 \\ 0 & 0 & \frac{1}{2}\end{array}\right)$ .

\begin{aligned} \boldsymbol{A}^{99} & =\boldsymbol{P}\left(\begin{array}{ccc} (-2)^{99} & 0 & 0 \\ 0 & (-1)^{99} & 0 \\ 0 & 0 & 0 \end{array}\right) \boldsymbol{P}^{-1}=\left(\begin{array}{lll} 1 & 1 & 3 \\ 2 & 1 & 2 \\ 0 & 0 & 2 \end{array}\right)\left(\begin{array}{ccc} -2^{99} & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{array}\right)\left(\begin{array}{ccc} -1 & 1 & \frac{1}{2} \\ 2 & -1 & -2 \\ 0 & 0 & \frac{1}{2} \end{array}\right) \\ & =\left(\begin{array}{ccc} 2^{99}-2 & 1-2^{99} & 2-2^{98} \\ 2^{100}-2 & 1-2^{100} & 2-2^{99} \\ 0 & 0 & 0 \end{array}\right) . \end{aligned}

这就是说，特征值，特征向量，方程组的解，基础解系，对角型，使用这几个概念互相配合，

竟然把一个矩阵要算99次的超大“工作”量，转换为了其矩阵元素的指数次方。 工作量大大的降低。

数学服务于物理

我们说数学是为物理服务的，在物理里，有大量二次运算，比如牛顿加速度运动定律 $m v^2 / 2$ ，电压电流 $U=I R ，$ 万有引力定律等等都是二次的。

数学服务于几何

从几何上看，更要研究二次型在中学的几何中我们学过，对于一元二次函数 $f(x)=a x^2$ 在二维平面上看我们有非常清晰的几何图形: 他就是过原点的抛物线: $a>0$ 开口向上， $a<0$ 开口向下， $a=0$ ，抛物线蜕化成直线 $x$ 轴。 $图片$

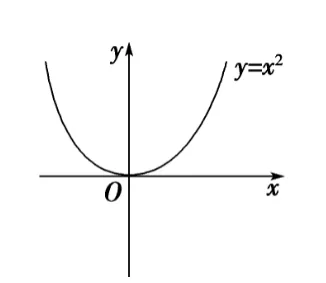
那么对于函数 $f(x)=a x^2+b x+c$ 图形呢? 我们依然清哳地知道, 他还是一个抛物线图像，只不过在横轴和纵轴方向上同时进行了平移，但图形趋势仍然相同。因为可以把它经过配方得到上面的形式: $f(x)=a x^2+b x+c=a\left(x+\frac{b}{2 a}\right)^2+\left(c-\frac{b^2}{4 a}\right)$

所以，一个多项式的图像，是由最高次幂决定的，后面低次幂仅是对图像上下左右进行变化。到这里我们有一个小小的初步结论, 就是函数的几何图形是合同的, 合同的意思是它们经过平移、变换后图形会完全重合。

既然是这样，如果是要考察几何图形性质的话，对于 $f(x)=a x^2+b x+c$ 类的函数我们只要考察 $f(x)=a x^2$ 的形式就可以了。这样可以简化运算，换句话说, 我们只需研究透了这个二次函数的性质，就能得到整体的性质 (这也可以认为是坐标映射)。

再如二元函数 $f(x, y)=a x^2+c y^2$ 的图形在三维空间中观看是鞍马面，我们大致能推断 $f(x)=a x^2+b x y+c y^2+d$ 函数图形经过旋转平移等应该和它 "长" 的类似。 $图片$

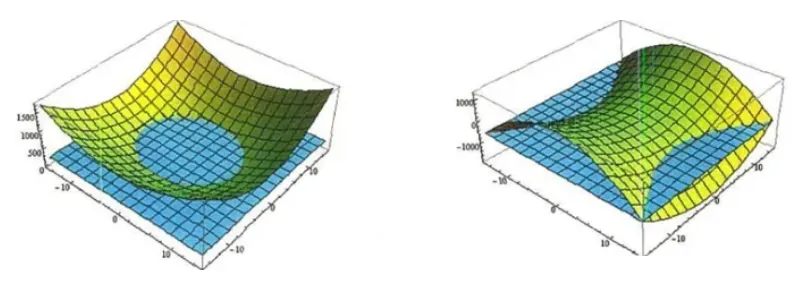
相比一次函数，二次函数要复杂、抽象的多，为此提出了矩阵的等价、相似与合同三大概念，我们会在附录2里进行简单概括，详见

在附录2：线性方程组、行列式、矩阵、向量组的关系理解矩阵的等价、相似与合同。

线性空间转换

正如一元二次方程 $ax^2+bx+c=0$ 一样，如果从解方程的角度看，他是解二次方程，但是如果从二次函数的视角看，他是一个抛物线。同样一个代数式，不同的视角会赋予不同的含义，最终会殊途同归。在上面介绍线性代数里，是从解方程的角度看待线性代数，目前主流观点是从线性空间理解线性代数，

如果说解方程是从微观视角看线性代数，那么图形变换则是从宏观视角理解线性代数。这就像，我们知道物质都是有原子或者分子组成，这是一个微观视角，但是当一个人生病后，去检测白细胞，红细胞，细胞本质上也是原子、分子组成的，但是在医学上从来不会说原子，分子，而是说细胞，或者说细胞是生物最小的基础单位(而原子不是生物上最小组成单位)。

我们在矩阵乘法里可以看到，两个矩阵相乘，本质是做一个线性变换。同纬度我们称作线性变换，不同维度称作线性映射。

矩阵 X 矩阵 = 同纬度变换

同维

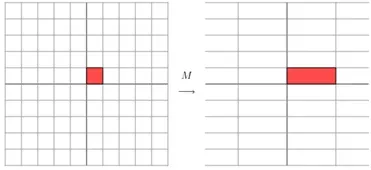
一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。比如说一个向量 $(1,1)$ 乘以下面的一个矩阵：

M=\left[\begin{array}{ll} 3 & 0 \\ 0 & 1 \end{array}\right]

他其实就是对向量进行了缩放，参考下图，可以看到图像变长了。 $图片$

降维

如果矩阵不满秩，作用在向量上会产生降维效果。

比如本来矩阵A包含了2个向量，这2个向量可以张成一个空间，但是一个矩阵B作用其上后，2个向量共线了，变成了一维向量。

\boldsymbol{C}=\boldsymbol{B} \boldsymbol{A}=\left(\begin{array}{ll} 2 & 1 \\ 4 & 2 \end{array}\right)\left(\begin{array}{ll} 1 & 3 \\ 2 & 2 \end{array}\right)=\left(\begin{array}{cc} 4 & 8 \\ 8 & 16 \end{array}\right)

$图片$

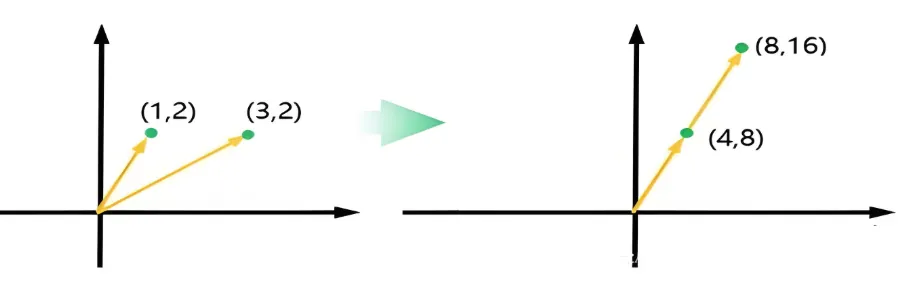
升维

相对的，矩阵升维用的不多，最常见的是平移

\begin{aligned} & x^{\prime}=x+t_x \\ & y^{\prime}=y+t_y \end{aligned}

平行虽然简单，但是平移却不是线性变换的，写成矩阵就是

\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]+\left[\begin{array}{l} t_x \\ t_y \end{array}\right]

为了统一变换操作，我们引入一个新的维度。对于二维的点 $(x, y)$ 我们可以增加一个维度，对于 2 维的点可以表示为 $(x, y, 1) ^T,$ 2维向量的 $(x, y, 0)^ T$ 。因此，一个点的平移可以用矩阵表示为：

\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ w^{\prime} \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{c} x+t_x \\ y+t_y \\ 1 \end{array}\right]

通过把2维升级为3维，就把非线性的转换为了线性的。

这种变换类似切边变换、反射变换等，在使用Photoshop进行图像处理时，可以进行各种修图，本质也是进行矩阵的一种变换。

$图片$ {width=500px}

我们将在矩阵乘法、矩阵的平移矩阵，旋转矩阵，缩放矩阵，线性变换，仿射变换，齐次坐标和奇异值分解介绍。

近世代数对数学的整体思考

参考下图:一个个数字或者物体被称作元素，元素放在一起组成了集合(这个高中就学过)，集合排在一起组成了空间，如果空间满足八大性质(交换律、结合律等)则被定义为线性空间。空间里元素的距离称为度量空间。我们需要一个尺子作为度量的基准，这个尺子被称为范数，含有范数的空间称为线性赋范空间，具备完备后称为巴拿赫空间。 $图片$

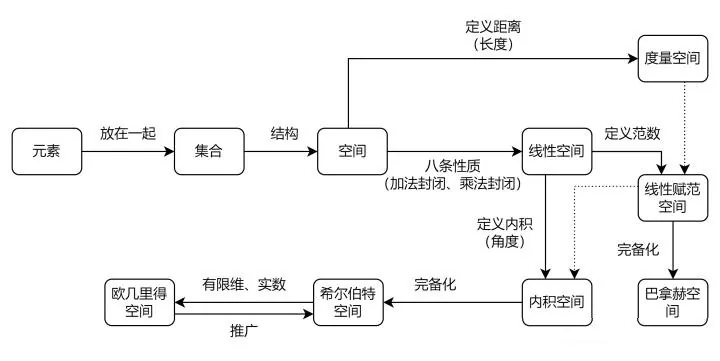
这里要强调一下封闭性，如果集合 $F$ 里的数进行加减乘除仍在 $F$ 里，则 $F$ 称为封闭数域，比如“全体有理数”就是一个封闭数域，因为任何有理数的加减乘除仍在有理数里，但是“全体整数”就不是封闭数域，因为两个数相除有可能是分数。详细介绍参加近世代数对数学的整体思考

如何学好线性代数

概念环环相扣是线性代数最大的特点，举例来说，与＂ $n$ 阶矩阵 $A$ 可逆＂这个概念等价的命题就有十多个： $n$ 阶矩阵 $A$ 可逆 $\Leftrightarrow A$ 的行列式的值不为 $0 \Leftrightarrow A$ 满秩等。这些等价命题原先是分散在各个章节中的，需要读者在学习过程中不断分析，归纳和总结。

线性代数变换的世界为你归纳了核心知识点的总结。