17._逆矩阵

逆矩阵引入

在数学里，数字有加减乘除运算，自然，我们想把这个运算规律推广到矩阵上。在矩阵里，前面介绍了矩阵的加减和乘法，只有除法没有说过。 在数字运算中, 除法是乘法的逆运算, 它可以通过求倒数来实现. 即若求数 $a$ 除以 $b(b \neq 0)$ 的商, 则只需求出 $b^{-1}=\frac{1}{b}$, 于是 $\frac{a}{b}=a b^{-1}$. 对矩阵我们也可以这样做, 先定义矩阵的逆阵, 然后将矩阵的除法归结为一个矩阵和另外一个矩阵的逆阵之积.

逆矩阵的定义

定义1 设 $\boldsymbol{A}$ 为 $n$ 阶方阵，如果存在 $n$ 阶方阵 $\boldsymbol{B}$ 使得

其中 $E$ 为 $n$ 阶单位方阵，则称矩阵 $A$ 是可逆的，矩阵 $B$ 称为 $A$ 的逆矩阵；否则称 $A$ 是不可逆的. 如果矩阵 $A$ 可逆，则 $A$ 的逆矩阵一定是唯一的. 这是因为，若矩阵 $B 、 C$ 都满足 $A B=B A=E ， A C=C A=E$ ，于是 $C=C E=C(A B)=(C A) B=E B=B$. 所以 $A$ 的逆矩阵一定是唯一的. $A$ 的逆矩阵记为 $A^{-1}$.

并非任一非零方阵都有逆阵． 比如，矩阵

就没有逆阵．因为对任一 $B =\left(b_{i j}\right)_{2 \times 2}$ ，有

$A B$ 不可能是单位阵．

矩阵的逆是什么

如果把矩阵的逆类比为数字中的倒数：应该是

数字：$ab=1 => b=\dfrac{1}{a}=a^{-1}$ 矩阵：$AB=E => B=\dfrac{1}{A}=A^{-1}$

但是，等等，因为矩阵一般不满足 $AB \neq BA$，写成倒数就会有问题，例如

$\dfrac{AB}{C}$ 到底表示的是 $ABC^{-1}$ 还是 $C^{-1}AB$ 会有歧义.

矩阵里，我们从不会说矩阵有除法运算，而是说有逆运算。但是在学习中，您完全可以把逆运算看成除法，这样很多推导会容易记忆的很多。

若方阵$A$得行列式$|A|=0$,则称$A$为奇异矩阵，也叫退化矩阵或降秩矩阵。

若方阵$A$得行列式$|A| \ne 0$,则称$A$非奇异矩阵，也叫非退化矩阵或非降秩矩阵。

把矩阵的逆想象为数字除法后，正像除非里分母不能为零，同样，逆矩阵里$|A| \neq 0$他是可逆的。 如果$|A| = 0$他就是不可逆。

矩阵可逆的充要条件

定理2 $n$ 阶方阵 $A$ 可逆的充分必要条件是 $|A| \neq 0$. 证明： $n$ 阶方阵 $A$ 可逆，则方阵 $A$ 行等价于单位阵 $E$ ，即 $A$ 可通过初等行变换化为单位阵 $E$. 一定存在一个数 $\lambda \neq 0$ ，使得 $|A|=\lambda|E|$. 而 $|E|=1$ ，因此 $|A|=\lambda \neq 0$. 反之，设 $|A| \neq 0$. 由于 $n$ 阶方阵 $A$ 可通过初等行变换化为行最简形矩阵 $R$ ， 因此存在一个数 $\lambda \neq 0$, 使得 $|A|=\lambda|R|$. 由 $|A| \neq 0$ 可得 $|R| \neq 0$ ，因此 $R$ 中没有全零行，从而 $R=E$. 也就是说，方阵 $A$ 行等价于单位阵 $E$ ，所以方阵 $A$ 可逆.

下面三个说法是等价的

A可逆 $\Leftrightarrow$ $Ax=0$只有零解 $\Leftrightarrow$ 与单位阵E等价

上面可以拆解为两个意思 ① $|A|=0$ 则 $Ax=0$有非零解 ② $|A|\ne 0$ 则 $Ax=0$只有零解

记忆技巧：零-非零， 非零-零，这个口诀在后面判断方程的解时经常用到，详见 对立与统一

可逆的几何意义

一个矩阵的逆，其几何意义就是“撤销”原矩阵所代表的线性变换。比如你往东走5米，可逆矩阵让你往西走5米，这样你又回到了原点。当你用一个矩阵 $A$ 乘以一个向量$x$（即 $A * x$），你实际上是在对这个向量进行一个操作，旋转、缩放或剪切变换，而逆矩阵相当于“撤销”这些操作。

缩放变换

矩阵 A： $[[2, 0], [0, 3]]$。这是一个将$x$方向放大2倍，$y$方向放大3倍的变换。 几何效果：一个正方形会被拉伸成一个 2x3 的矩形。 逆矩阵 A⁻¹： $[[1/2, 0], [0, 1/3]]$。 逆的几何意义：将变换后的图形在x方向缩小到1/2，在y方向缩小到1/3。这样，那个被拉伸的 2x3 的矩形就准确地变回了原来的正方形。

旋转变换

矩阵 A： [[0, -1], [1, 0]]。这是一个将向量逆时针旋转90度的变换。 几何效果：一个指向右边的箭头，会变成指向上边的箭头。 逆矩阵 A⁻¹： [[0, 1], [-1, 0]]（这恰好也是 A 的转置，对于旋转矩阵，其逆等于其转置）。 逆的几何意义：将变换后的图形顺时针旋转90度。这样，指向上边的箭头就又变回了指向右边的箭头。

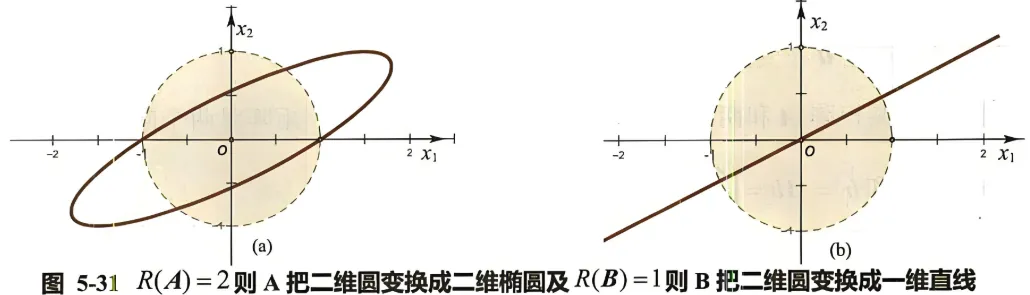
并非所有矩阵都有逆矩阵，有些矩阵没有逆矩阵的本质是：数据丢失。

比如一个矩阵作用在一个单位圆上，单位圆变成了椭圆，因此后续能找到一个逆矩阵再把椭圆变成了圆。 但是如果矩阵作用在单位圆上，单位圆变成了直线，那么后续就无法找到一个逆矩阵，把直线还原成圆，详见 向量的秩

逆矩阵的性质

1 若 $A$ 可逆，则 $A^{-1}$ 也可逆，并且 $\left(A^{-1}\right)^{-1}=A$ ； 2 若矩阵 $A_1, A_2, \cdots, A_s$ 都可逆，则它们的乘积 $A_1 A_2 \cdots A_s$ 也可逆，并且 $\left(A_1 A_2 \cdots A_s\right)^{-1}=A_s^{-1} \cdots A_2^{-1} A_1^{-1} ;$ 3 若 $A$ 可逆，则 $A^{\mathrm{T}}$ 也可逆，并且 $\left(A^{\mathrm{T}}\right)^{-1}=\left(A^{-1}\right)^{\mathrm{T}}$ ； 4 若 $A$ 可逆并且数 $k \neq 0$ ，则 $k \boldsymbol{A}$ 也可逆，并且 $(k \boldsymbol{A})^{-1}=k^{-1} A^{-1}$.

5.分块矩阵的逆 对于分块矩阵的逆，详见 分块矩阵

例 设 A 为 m 阶可逆矩阵， B 为 n 阶可逆矩阵，则可逆分块矩阵 $D=\left(\begin{array}{ll}O & A \\ B & O\end{array}\right)$ 的逆矩阵是

A. $\left(\begin{array}{cc}A^{-1} & O \\ O & B^{-1}\end{array}\right)$

B. $\left(\begin{array}{cc}O & B^{-1} \\ A^{-1} & O\end{array}\right)$

C. $\left(\begin{array}{cc}B^{-1} & O \\ O & A^{-1}\end{array}\right)$

D. $\left(\begin{array}{cc}O & A^{-1} \\ B^{-1} & O\end{array}\right)$

答案是 B

例若矩阵 $A$ 有全零行 (全零列)，那么矩阵 $A$ 一定不可逆. 证明 假设矩阵 $A$ 的第 $i$ 行是全零行，则对任何一个矩阵 $B$ ，矩阵 $A B$ 的第 $i$ 行总是全为零， 从而不存在矩阵 $B$ 使得 $A B=B A=E$ ，所以矩阵 $A$ 不可逆. 类似可证，若矩阵 $A$ 有全零列，那么矩阵 $A$ 一定不可逆.

例设 $A^k=\boldsymbol{O}$ ( $k$ 为正整数), 证明: $(E-A)^{-1}=E+A+A^2+\cdots+A^{k-1}$. 证明 因为 $A^k=O$, 于是

所以 $E-A$ 可逆，且 $(E-A)^{-1}=E+A+A^2+\cdots+A^{k-1}$.

例 判断下列矩阵是否可逆: (1) $A=\left(\begin{array}{ccc}-1 & 1 & -1 \\ 1 & -1 & -1 \\ -1 & -1 & 1\end{array}\right)$; (2) $B=\left(\begin{array}{ccc}2 & 1 & -3 \\ -1 & 0 & 1 \\ 1 & -2 & 1\end{array}\right)$.

解：(1)因为 $\quad|\boldsymbol{A}|=\left|\begin{array}{ccc}-1 & 1 & -1 \\ 1 & -1 & -1 \\ -1 & -1 & 1\end{array}\right|=\left|\begin{array}{ccc}-1 & 1 & -1 \\ 0 & 0 & -2 \\ 0 & -2 & 2\end{array}\right|=-\left|\begin{array}{ccc}-1 & 1 & -1 \\ 0 & -2 & 2 \\ 0 & 0 & -2\end{array}\right|=4 \neq 0$, 所以矩阵 $A$ 可逆. (2) 因为 $|\boldsymbol{B}|=\left|\begin{array}{ccc}2 & 1 & -3 \\ -1 & 0 & 1 \\ 1 & -2 & 1\end{array}\right|=-\left|\begin{array}{ccc}-1 & 0 & 1 \\ 2 & 1 & -3 \\ 1 & -2 & 1\end{array}\right|=-\left|\begin{array}{ccc}-1 & 0 & 1 \\ 0 & 1 & -1 \\ 0 & -2 & 2\end{array}\right|=0$, 所以矩阵 $B$ 不可逆.

例 $n$ 阶方阵 $\boldsymbol{A}_n$ 满足 $\boldsymbol{A}^2+2 \boldsymbol{A}-3 \boldsymbol{E}=\boldsymbol{O}$ ，证明 $\boldsymbol{A}, \boldsymbol{A}+2 \boldsymbol{E}$ ， $\boldsymbol{A}+4 \boldsymbol{E}$ 可逆，并求其逆．

证明：由 $\boldsymbol{A}^2+2 \boldsymbol{A}-3 \boldsymbol{E}=\boldsymbol{O}$ 有

从而 $\frac{1}{3} \boldsymbol{A}(\boldsymbol{A}+2 \boldsymbol{E})=\boldsymbol{E}$ ．由上述推论知 $\boldsymbol{A}, \boldsymbol{A}+2 \boldsymbol{E}$ 均可逆，且 $\boldsymbol{A}^{-1}= \frac{1}{3}(\boldsymbol{A}+2 \boldsymbol{E}),(\boldsymbol{A}+2 \boldsymbol{E})^{-1}=\frac{1}{3} \boldsymbol{A}$.

由 $\boldsymbol{A}^2+2 \boldsymbol{A}-3 \boldsymbol{E}=\boldsymbol{O}$ 有 $\boldsymbol{A}^2+4 \boldsymbol{A}-2 \boldsymbol{A}-8 \boldsymbol{E}=-5 \boldsymbol{E}$ ，分解因式有

由上述推论知， $\boldsymbol{A}+4 \boldsymbol{E}$ 可逆，且 $(\boldsymbol{A}+4 \boldsymbol{E})^{-1}=-\frac{1}{5}(\boldsymbol{A}-2 \boldsymbol{E})$ ．

在上例里，要求一个矩阵可逆，要尽可能“凑成”他的逆矩阵，然后证明 $AA^{-1}=E$

逆矩阵的求法

逆矩阵通常有两种求法 （1）伴随矩阵法 （2）初等行变换法 （3）初等列变换法

伴随矩阵法求解逆矩阵

伴随矩阵的性质：

利用这个性质可以求矩阵的逆。

例求

的伴随矩阵

注：本节内容涉及 伴随矩阵 的求法。

解：

于是$A$的伴随矩阵为

$A$得逆矩阵

利用上面的结论可以解决考试常见的试题。

例设 $\boldsymbol{A}$ 是一个 3 阶方阵，并设 $|\boldsymbol{A}|=2$ ．求 $\left|4 \boldsymbol{A}^{-1}+\boldsymbol{A}^*\right|$ ．

解．已知 $\boldsymbol{A}$ 是一个 3 阶方阵，并且 $|\boldsymbol{A}|=2$ ，那么 $\left|\boldsymbol{A}^{-1}\right|=\frac{1}{2}$ ，并且 $\boldsymbol{A}^*=|\boldsymbol{A}| \boldsymbol{A}^{-1}=2 \boldsymbol{A}^{-1}$ 。于是

初等行变换法求逆矩阵

定理 $n \times n$ 矩阵 $A$ 是可逆的, $A$ 行等价于 $I_n$, 这时, 把 $A$ 变为 $I_n$ 的一系列初等行变换同时也会把 $I_n$ 变成 $A^{-1}$ 。

证 设 $A$ 是可逆矩阵, 则对任意 $b$, 方程 $A x = b$ 有解 ， $A$ 在每一行有主元位置 , 因 $A$ 是方阵, 这 $n$ 个主元位置必在对角线上. 这就是说 $A$ 的简化阶梯形是 $I_n$, 即 $A \sim I_n$.

反之, 若 $A \sim I_n$, 因每一步行变换对应于左乘一个初等矩阵, 就是说, 存在初等矩阵 $E_1, \cdots, E_p$使

即

因为 $E_p \cdots E_1$ 是可逆矩阵的乘积, 因此也是可逆矩阵, 由 (1) 式推出

于是 $A$ 是可逆的, 因它是可逆矩阵的逆 , 同样有

于是 $A^{-1}=E_p \cdots E_1 \cdot I_n$, 这就是说, $A^{-1}$ 可由依次以 $E_1, \cdots, E_p$ 作用于 $I_n$ 而得到, 它们就是上 式中把 $A$ 变为 $I_n$ 的同一行变换序列.

由此得到如下结论：

若$A$是一个$n$阶矩阵,把$A$和单位阵$E$合在一起，即 $[A \mid E]$ 然后进行初等行变换，把左边$A$变换为$E$，而右侧就是$A$得逆矩阵$A^{-1}$ 即得 $[E \mid A^{-1}]$ 。

例 求下面矩阵的逆矩阵

解：把矩阵$A$和单位矩阵$E$进行合并 构造增广矩阵

然后使用初等行变换，把左边矩阵A化为单位矩阵E

第一步：第一行$-5$倍加到第三行

用第二行消去第一行和第三行。

用第三行消去第一行和第二行。

此时左侧已经是单位矩阵，右侧就是逆矩阵，所以

上面左侧化成单位矩阵的具体介绍请参考 阶梯形矩阵的求法

例已知 $\boldsymbol{A}^2=\left(\begin{array}{rrr}2 & -1 & 0 \\ 7 & -3 & 0 \\ 0 & 0 & 9\end{array}\right), \boldsymbol{A}^3=\left(\begin{array}{rrr}-1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -27\end{array}\right)$ ，求 $\boldsymbol{A}$ ．

【解】因为 $\boldsymbol{A}^2 \cdot \boldsymbol{A}=\boldsymbol{A}^3$ ，且 $\boldsymbol{A}^2$ 可逆，所以

【注】若能运用下述结果，则可提高运算速度：

用初等列变换求逆矩阵（了解即可）

若$A$是一个$n$阶矩阵,把$A$和单位阵$E$合在一起，即 $\binom{ A }{ E }$ 然后进行初等列变换，把上边$A$变换为$E$，则下面就是$A$得逆矩阵$A^{-1}$ 即得 $\binom{ E }{ A ^{-1}}$ 。

我们几乎不用列变换求逆矩阵，此处稍微了解即可

例求 矩阵A的逆矩阵。

解：把矩阵A和单位E竖着排列起来

使用初等列变换（只能使用列变换），把上面矩阵化为E

上面部分：

• 第1列 $[1,0,2]^T$ 不动

• 第3列： 原来 $[2,0,1]^T$ 减去 $2\times [1,0,2]^T = [2,0,1]^T - [2,0,4]^T = [0,0,-3]^T$

得到：

继续化简，具体过程略，可以得到

最终的都逆矩阵