分块矩阵的运算 (1) 分块矩阵加 (减) 运算:
设 A 、 B A 、 B A 、 B m × n m \times n m × n
A = ( A 11 A 12 ⋯ A t r A 21 A 22 ⋯ A t ⋮ ⋮ ⋮ A t 1 A t 2 ⋯ A t t ) , B = ( B 11 B 12 ⋯ B 1 t B 22 B 22 ⋯ B 2 t ⋮ ⋮ ⋮ B t 1 B t 2 ⋯ B B t ) , A=\left(\begin{array}{cccc}
A_{11} & A_{12} & \cdots & A_{t r} \\
A_{21} & A_{22} & \cdots & A_t \\
\vdots & \vdots & & \vdots \\
A_{t 1} & A_{t 2} & \cdots & A_{t t}
\end{array}\right), \quad B=\left(\begin{array}{cccc}
B_{11} & B_{12} & \cdots & B_{1 t} \\
B_{22} & B_{22} & \cdots & B_{2 t} \\
\vdots & \vdots & & \vdots \\
B_{t 1} & B_{t 2} & \cdots & B_{B t}
\end{array}\right), A = A 11 A 21 ⋮ A t 1 A 12 A 22 ⋮ A t 2 ⋯ ⋯ ⋯ A t r A t ⋮ A tt , B = B 11 B 22 ⋮ B t 1 B 12 B 22 ⋮ B t 2 ⋯ ⋯ ⋯ B 1 t B 2 t ⋮ B Bt , 其中 A i j A_{i j} A ij B i j B_{i j} B ij
A ± B = ( A 11 ± B 11 A 12 ± B 12 ⋯ A t t ± B 1 t A 21 ± B 21 A 22 ± B 22 ⋯ A 2 t ± B 2 t ⋮ ⋮ ⋮ A s 1 ± B s 1 A s 2 ± B s 2 ⋯ A s t ± B s t ) . A \pm B=\left(\begin{array}{cccc}
A_{11} \pm B_{11} & A_{12} \pm B_{12} & \cdots & A_{t t} \pm B_{1 t} \\
A_{21} \pm B_{21} & A_{22} \pm B_{22} & \cdots & A_{2 t} \pm B_{2 t} \\
\vdots & \vdots & & \vdots \\
A_{s 1} \pm B_{s 1} & A_{s 2} \pm B_{s 2} & \cdots & A_{s t} \pm B_{s t}
\end{array}\right) . A ± B = A 11 ± B 11 A 21 ± B 21 ⋮ A s 1 ± B s 1 A 12 ± B 12 A 22 ± B 22 ⋮ A s 2 ± B s 2 ⋯ ⋯ ⋯ A tt ± B 1 t A 2 t ± B 2 t ⋮ A s t ± B s t . 例1 求矩阵 A = ( 1 0 0 0 0 0 0 0 2 0 0 0 1 1 0 3 ) A=\left(\begin{array}{llll}1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 \\ 1 & 1 & 0 & 3\end{array}\right) A = 1 0 2 1 0 0 0 1 0 0 0 0 0 0 0 3 B = ( − 2 0 1 0 0 − 1 0 1 1 1 − 4 2 2 1 3 − 1 ) B=\left(\begin{array}{cccc}-2 & 0 & 1 & 0 \\ 0 & -1 & 0 & 1 \\ 1 & 1 & -4 & 2 \\ 2 & 1 & 3 & -1\end{array}\right) B = − 2 0 1 2 0 − 1 1 1 1 0 − 4 3 0 1 2 − 1 A + B A+B A + B A A A B B B
A = ( 1 0 0 0 0 0 0 0 2 0 0 0 1 1 0 3 ) = ( A 1 o A 2 A 3 ) , B = ( − 2 0 1 0 0 − 1 0 1 1 − 4 2 2 − 1 0 − 3 ) = ( B 1 B 2 B 3 B 4 ) \boldsymbol{A}=\left(\begin{array}{c:ccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
2 & 0 & 0 & 0 \\
\hdashline 1 & 1 & 0 & 3
\end{array}\right)=\left(\begin{array}{ll}
\boldsymbol{A}_1 & \boldsymbol{o} \\
\boldsymbol{A}_2 & \boldsymbol{A}_3
\end{array}\right), \quad \boldsymbol{B}=\left(\begin{array}{c:ccc}
-2 & 0 & 1 & 0 \\
0 & -1 & 0 & 1 \\
\hdashline & 1 & -4 & 2 \\
\hdashline 2 & -1 & 0 & -3
\end{array}\right)=\left(\begin{array}{ll}
\boldsymbol{B}_1 & \boldsymbol{B}_2 \\
\boldsymbol{B}_3 & \boldsymbol{B}_4
\end{array}\right) A = 1 0 2 1 0 0 0 1 0 0 0 0 0 0 0 3 = ( A 1 A 2 o A 3 ) , B = − 2 0 2 0 − 1 1 − 1 1 0 − 4 0 0 1 2 − 3 = ( B 1 B 3 B 2 B 4 ) F是, A + B = ( A 1 O A 2 A 3 ) + ( B 1 B 2 B 3 B 4 ) = ( A 1 + B 1 O + B 2 A 2 + B 3 A 3 + B 4 ) = ( A 1 + B 1 B 2 A 2 + B 3 A 3 + B 4 ) \quad A+B=\left(\begin{array}{ll}A_1 & O \\ A_2 & A_3\end{array}\right)+\left(\begin{array}{ll}B_1 & B_2 \\ B_3 & B_4\end{array}\right)=\left(\begin{array}{cc}A_1+B_1 & O+B_2 \\ A_2+B_3 & A_3+B_4\end{array}\right)=\left(\begin{array}{cc}A_1+B_1 & B_2 \\ A_2+B_3 & A_3+B_4\end{array}\right) A + B = ( A 1 A 2 O A 3 ) + ( B 1 B 3 B 2 B 4 ) = ( A 1 + B 1 A 2 + B 3 O + B 2 A 3 + B 4 ) = ( A 1 + B 1 A 2 + B 3 B 2 A 3 + B 4 )
A 1 + B 1 = ( 1 0 2 ) + ( − 2 0 1 ) = ( − 1 0 3 ) , A + B = ( − 1 0 1 0 0 − 1 0 1 3 1 − 4 2 3 0 0 0 ) \begin{gathered}
\boldsymbol{A}_1+\boldsymbol{B}_1=\left(\begin{array}{l}
1 \\
0 \\
2
\end{array}\right)+\left(\begin{array}{c}
-2 \\
0 \\
1
\end{array}\right)=\left(\begin{array}{c}
-1 \\
0 \\
3
\end{array}\right), \\
\boldsymbol{A}+\boldsymbol{B}=\left(\begin{array}{c|ccc}
-1 & 0 & 1 & 0 \\
0 & -1 & 0 & 1 \\
3 & 1 & -4 & 2 \\
\hline 3 & 0 & 0 & 0
\end{array}\right)
\end{gathered} A 1 + B 1 = 1 0 2 + − 2 0 1 = − 1 0 3 , A + B = − 1 0 3 3 0 − 1 1 0 1 0 − 4 0 0 1 2 0 A 2 + B 3 = 1 + 2 = 3 , A 3 + B 4 = ( 1 , 0 , 3 ) + ( − 1 , 0 , − 3 ) = ( 0 , 0 , 0 ) , \boldsymbol{A}_2+\boldsymbol{B}_3=1+2=3, \quad \boldsymbol{A}_3+\boldsymbol{B}_4=(1,0,3)+(-1,0,-3)=(0,0,0), A 2 + B 3 = 1 + 2 = 3 , A 3 + B 4 = ( 1 , 0 , 3 ) + ( − 1 , 0 , − 3 ) = ( 0 , 0 , 0 ) , (2) 分块矩阵的数乘运算:
矩阵的分块方式没有特别规定,对任意的分块 A = ( A 11 A 12 ⋯ A t A 21 A 22 ⋯ A 2 n ⋮ ⋮ ⋮ A t 1 A t 2 ⋯ A t i ) A=\left(\begin{array}{cccc}A_{11} & A_{12} & \cdots & A_t \\ A_{21} & A_{22} & \cdots & A_{2 n} \\ \vdots & \vdots & & \vdots \\ A_{t 1} & A_{t 2} & \cdots & A_{t i}\end{array}\right) A = A 11 A 21 ⋮ A t 1 A 12 A 22 ⋮ A t 2 ⋯ ⋯ ⋯ A t A 2 n ⋮ A t i
k A = ( k A 11 k A 12 … k A 1 k A 21 k A 22 … k A 2 t ⋮ ⋮ ⋮ k A 11 k A 12 … k A t u ) . k A=\left(\begin{array}{cccc}
k A_{11} & k A_{12} & \ldots & k A_1 \\
k A_{21} & k A_{22} & \ldots & k A_{2 t} \\
\vdots & \vdots & & \vdots \\
k A_{11} & k A_{12} & \ldots & k A_{t u}
\end{array}\right) . k A = k A 11 k A 21 ⋮ k A 11 k A 12 k A 22 ⋮ k A 12 … … … k A 1 k A 2 t ⋮ k A t u . 在矩阵的数乘运算中,对矩阵的分块可以根据矩阵本身的特点而定.
(3) 分块矩阵的乘法:
设 A \boldsymbol{A} A m × s m \times s m × s B \boldsymbol{B} B s × n s \times n s × n A \boldsymbol{A} A B \boldsymbol{B} B A A A B B B A 1 , A i 2 , ⋯ , A i k A_1, A_{i 2}, \cdots, A_{i k} A 1 , A i 2 , ⋯ , A ik B 1 j , B 2 j , ⋯ , B i j B_{1 j}, B_{2 j}, \cdots, B_{i j} B 1 j , B 2 j , ⋯ , B ij
C i j = ∑ t = 1 k A i t B i j = A i t B 1 j + A i 2 B 2 j + ⋯ + A i k B i j C_{i j}=\sum_{t=1}^k A_{i t} B_{i j}=A_{i t} B_{1 j}+A_{i 2} B_{2 j}+\cdots+A_{i k} B_{i j} C ij = t = 1 ∑ k A i t B ij = A i t B 1 j + A i 2 B 2 j + ⋯ + A ik B ij 例 2 设 A = ( 1 0 1 0 − 1 1 0 1 − 1 0 0 0 0 − 1 0 0 ) , B = ( 1 2 0 0 − 2 1 0 0 1 0 0 − 1 0 1 − 1 0 ) A=\left(\begin{array}{cccc}1 & 0 & 1 & 0 \\ -1 & 1 & 0 & 1 \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0\end{array}\right), B=\left(\begin{array}{cccc}1 & 2 & 0 & 0 \\ -2 & 1 & 0 & 0 \\ 1 & 0 & 0 & -1 \\ 0 & 1 & -1 & 0\end{array}\right) A = 1 − 1 − 1 0 0 1 0 − 1 1 0 0 0 0 1 0 0 , B = 1 − 2 1 0 2 1 0 1 0 0 0 − 1 0 0 − 1 0 A B A B A B A A A B B B
A = ( 1 0 1 0 − 1 1 0 1 − 1 0 0 0 0 − 1 0 0 ) = ( A 11 E − E o ) , B = ( 1 2 0 0 − 2 1 0 0 1 0 0 − 1 0 1 − 1 0 ) = ( B 11 o E B 22 ) . A B = ( A 11 E − E O ) ( B 11 o E B 22 ) = ( A 1 B 11 + E 2 A 1 O + E B 2 − E B 11 + O E − E O + O B 22 ) = ( A 11 B 11 + E B 22 − B 11 O ) . \begin{aligned}
& A=\left(\begin{array}{cc|cc}
1 & 0 & 1 & 0 \\
-1 & 1 & 0 & 1 \\
\hline-1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0
\end{array}\right)=\left(\begin{array}{cc}
\boldsymbol{A}_{11} & \boldsymbol{E} \\
-\boldsymbol{E} & \boldsymbol{o}
\end{array}\right), \quad B=\left(\begin{array}{cc|cc}
1 & 2 & 0 & 0 \\
-2 & 1 & 0 & 0 \\
\hline 1 & 0 & 0 & -1 \\
0 & 1 & -1 & 0
\end{array}\right)=\left(\begin{array}{cc}
\boldsymbol{B}_{11} & \boldsymbol{o} \\
\boldsymbol{E} & \boldsymbol{B}_{22}
\end{array}\right) . \\
& A B=\left(\begin{array}{cc}
A_{11} & E \\
-E & O
\end{array}\right)\left(\begin{array}{ll}
B_{11} & o \\
E & B_{22}
\end{array}\right)=\left(\begin{array}{cc}
A_1 B_{11}+E^2 & A_1 \boldsymbol{O}+E B_2 \\
-E B_{11}+O E & -E O+O B_{22}
\end{array}\right)=\left(\begin{array}{cc}
A_{11} B_{11}+E & B_{22} \\
-B_{11} & O
\end{array}\right) . \\
&
\end{aligned} A = 1 − 1 − 1 0 0 1 0 − 1 1 0 0 0 0 1 0 0 = ( A 11 − E E o ) , B = 1 − 2 1 0 2 1 0 1 0 0 0 − 1 0 0 − 1 0 = ( B 11 E o B 22 ) . A B = ( A 11 − E E O ) ( B 11 E o B 22 ) = ( A 1 B 11 + E 2 − E B 11 + OE A 1 O + E B 2 − EO + O B 22 ) = ( A 11 B 11 + E − B 11 B 22 O ) . 而
A 11 B 11 + E = ( 1 0 − 1 1 ) ( 1 2 − 2 1 ) + ( 1 0 0 1 ) = ( 1 2 − 3 − 1 ) + ( 1 0 0 1 ) = ( 2 2 − 3 0 ) , − B 11 = ( − 1 − 2 2 − 1 ) A_{11} B_{11}+E=\left(\begin{array}{cc}
1 & 0 \\
-1 & 1
\end{array}\right)\left(\begin{array}{cc}
1 & 2 \\
-2 & 1
\end{array}\right)+\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)=\left(\begin{array}{cc}
1 & 2 \\
-3 & -1
\end{array}\right)+\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)=\left(\begin{array}{cc}
2 & 2 \\
-3 & 0
\end{array}\right), \quad-B_{11}=\left(\begin{array}{cc}
-1 & -2 \\
2 & -1
\end{array}\right) A 11 B 11 + E = ( 1 − 1 0 1 ) ( 1 − 2 2 1 ) + ( 1 0 0 1 ) = ( 1 − 3 2 − 1 ) + ( 1 0 0 1 ) = ( 2 − 3 2 0 ) , − B 11 = ( − 1 2 − 2 − 1 ) 所以
A B = ( 2 2 0 − 1 − 3 0 − 1 0 − 1 − 2 0 0 2 − 1 0 0 ) . A B=\left(\begin{array}{cc|cc}
2 & 2 & 0 & -1 \\
-3 & 0 & -1 & 0 \\
\hline-1 & -2 & 0 & 0 \\
2 & -1 & 0 & 0
\end{array}\right) . A B = 2 − 3 − 1 2 2 0 − 2 − 1 0 − 1 0 0 − 1 0 0 0 . (4) 分块矩阵的转置:
A T = ( A 11 T A 21 T ⋯ A r 1 T A 12 T A 22 T ⋯ A r 2 T ⋮ ⋮ ⋱ ⋮ A 1 s T A 2 s T ⋯ A r s T ) A^T = \begin{pmatrix}
A_{11}^T & A_{21}^T & \cdots & A_{r1}^T \\
A_{12}^T & A_{22}^T & \cdots & A_{r2}^T \\
\vdots & \vdots & \ddots & \vdots \\
A_{1s}^T & A_{2s}^T & \cdots & A_{rs}^T
\end{pmatrix} A T = A 11 T A 12 T ⋮ A 1 s T A 21 T A 22 T ⋮ A 2 s T ⋯ ⋯ ⋱ ⋯ A r 1 T A r 2 T ⋮ A rs T 即子块矩阵转置,同时子块位置也关于主对角线对称交换。
(5) 分块对角阵
设 A A A n n n A A A
即 A = ( A 1 o ⋯ o o A 2 ⋯ o ⋮ ⋮ ⋱ ⋮ o o ⋯ A t ) , \text { 即 } A=\left(\begin{array}{cccc}
A_1 & o & \cdots & o \\
o & A_2 & \cdots & o \\
\vdots & \vdots & \ddots & \vdots \\
o & o & \cdots & A_t
\end{array}\right) \text {, } 即 A = A 1 o ⋮ o o A 2 ⋮ o ⋯ ⋯ ⋱ ⋯ o o ⋮ A t , 其中 A i ( i = 1 , 2 , ⋯ , t ) A_i(i=1,2, \cdots, t) A i ( i = 1 , 2 , ⋯ , t )
例设 e i = ( 0 , ⋯ , 0 , 1 , 0 , ⋯ , 0 ) T e_i=(0, \cdots, 0,1,0, \cdots, 0)^{\mathrm{T}} e i = ( 0 , ⋯ , 0 , 1 , 0 , ⋯ , 0 ) T i i i n n n E n = ( e 1 , e 2 , ⋯ , e n ) E_n=\left(e_1, e_2, \cdots, e_n\right) E n = ( e 1 , e 2 , ⋯ , e n ) A A A A = ( A 1 , A 2 , ⋯ , A n ) A=\left(A_1, A_2, \cdots, A_n\right) A = ( A 1 , A 2 , ⋯ , A n ) A k A_k A k A A A k k k
( A 1 , A 2 , ⋯ , A n ) = A = A E = A ( e 1 , e 2 , ⋯ , e n ) = ( A e 1 , A e 2 , ⋯ , A e n ) , \left(\begin{array}{lll}
A_1, & A_2, \cdots, & A_n
\end{array}\right)=A=A E=A\left(e_1, e_2, \cdots, e_n\right)=\left(\begin{array}{lll}
A e_1, & A e_2, \cdots, & A e_n
\end{array}\right), ( A 1 , A 2 , ⋯ , A n ) = A = A E = A ( e 1 , e 2 , ⋯ , e n ) = ( A e 1 , A e 2 , ⋯ , A e n ) , 从而有
A e k = A k ( k = 1 , 2 , ⋯ , n ) , \boldsymbol{A} \boldsymbol{e}_k=\boldsymbol{A}_k(k=1,2, \cdots, n), A e k = A k ( k = 1 , 2 , ⋯ , n ) , 即 A e k \boldsymbol{A} \boldsymbol{e}_k A e k A \boldsymbol{A} A k k k e k T A \boldsymbol{e}_k^{\mathrm{T}} A e k T A A A A k k k e k T A e l = a k l \boldsymbol{e}_k^{\mathrm{T}} A e_l=a_{k l} e k T A e l = a k l A A A ( k , l ) (k, l) ( k , l )
例设 A A A m × n m \times n m × n n × 1 n \times 1 n × 1 α \alpha α A α = O A \boldsymbol{\alpha}=\boldsymbol{O} A α = O A = 0 A=0 A = 0 α \boldsymbol{\alpha} α α \boldsymbol{\alpha} α e j ( j = 1 , 2 , ⋯ , n ) e_j(j=1,2, \cdots, n) e j ( j = 1 , 2 , ⋯ , n )
A α = A e j = A j = O ( j = 1 , 2 , ⋯ , n ) , \boldsymbol{A} \boldsymbol{\alpha}=\boldsymbol{A} \boldsymbol{e}_j=\boldsymbol{A}_j=\boldsymbol{O}(j=1,2, \cdots, n), A α = A e j = A j = O ( j = 1 , 2 , ⋯ , n ) , 所以 A = O \boldsymbol{A}=\boldsymbol{O} A = O
分块矩阵的逆 (1)A A A A = ( A 11 A 22 ⋱ A s s ) s × s ∈ M n A=\left(\begin{array}{llll}A_{11} & & & \\ & A_{22} & & \\ & & \ddots & \\ & & & A_{s s}\end{array}\right)_{s \times s} \in M_n A = A 11 A 22 ⋱ A ss s × s ∈ M n A i j ( i = 1 , 2 , ⋯ s ) A_{i j}(i=1,2, \cdots s) A ij ( i = 1 , 2 , ⋯ s )
A − 1 = ( A 11 − 1 A 22 − 1 ⋱ A s − 1 ) A^{-1}=\left(\begin{array}{llll}
A_{11}^{-1} & & & \\
& A_{22}^{-1} & & \\
& & \ddots & \\
& & & A_s^{-1}
\end{array}\right) A − 1 = A 11 − 1 A 22 − 1 ⋱ A s − 1 (2)A A A A = ( B D 0 C ) ∈ M m + n , m + n A=\left(\begin{array}{cc}B & D \\ 0 & C\end{array}\right) \in M_{m+n, m+n} A = ( B 0 D C ) ∈ M m + n , m + n B ∈ M m , C ∈ B \in M_m, C \in B ∈ M m , C ∈ M n M_n M n B , C B, C B , C
A − 1 = ( B − 1 − B − 1 D C − 1 0 C − 1 ) A^{-1}=\left(\begin{array}{cc}
B^{-1} & -B^{-1} D C^{-1} \\
0 & C^{-1}
\end{array}\right) A − 1 = ( B − 1 0 − B − 1 D C − 1 C − 1 ) 如果 A = ( B 0 D C ) A=\left(\begin{array}{ll}B & 0 \\ D & C\end{array}\right) A = ( B D 0 C ) A − 1 = ( B − 1 0 − C − 1 D B − 1 C − 1 ) A^{-1}=\left(\begin{array}{cc}B^{-1} & 0 \\ -C^{-1} D B^{-1} & C^{-1}\end{array}\right) A − 1 = ( B − 1 − C − 1 D B − 1 0 C − 1 )
上面结论可以简单记忆为
[ B O D C ] − 1 = [ B − 1 O − C − 1 D B − 1 C − 1 ] , [ B D O C ] − 1 = [ B − 1 − B − 1 D C − 1 O C − 1 ] , [ O B C D ] − 1 = [ − C − 1 D B − 1 C − 1 B − 1 O ] , [ D B C O ] − 1 = [ O C − 1 B − 1 − B − 1 D C − 1 ] \begin{aligned}
& {\left[\begin{array}{ll}
B & O \\
D & C
\end{array}\right]^{-1}=\left[\begin{array}{cc}
B ^{-1} & O \\
- C ^{-1} D B ^{-1} & C ^{-1}
\end{array}\right],\left[\begin{array}{ll}
B & D \\
O & C
\end{array}\right]^{-1}=\left[\begin{array}{cc}
B ^{-1} & - B ^{-1} D C ^{-1} \\
O & C ^{-1}
\end{array}\right],} \\
& {\left[\begin{array}{ll}
O & B \\
C & D
\end{array}\right]^{-1}=\left[\begin{array}{cc}
- C ^{-1} D B ^ { - 1 } & C ^{-1} \\
B ^{-1} & O
\end{array}\right],\left[\begin{array}{ll}
D & B \\
C & O
\end{array}\right]^{-1}=\left[\begin{array}{cc}
O & C ^{-1} \\
B ^{-1} & - B ^{-1} D C ^{-1}
\end{array}\right]}
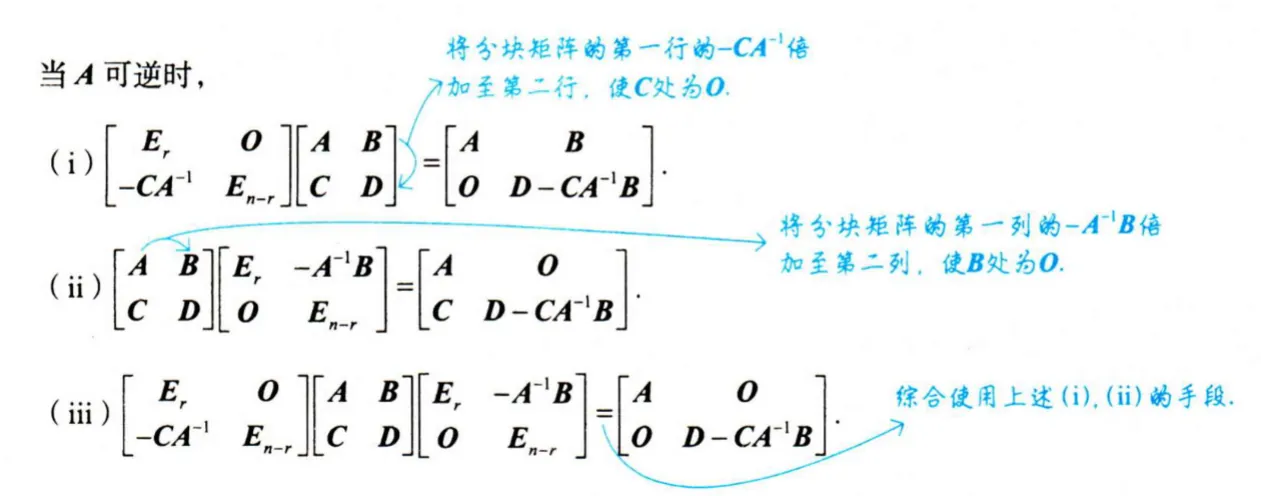
\end{aligned} [ B D O C ] − 1 = [ B − 1 − C − 1 D B − 1 O C − 1 ] , [ B O D C ] − 1 = [ B − 1 O − B − 1 D C − 1 C − 1 ] , [ O C B D ] − 1 = [ − C − 1 D B − 1 B − 1 C − 1 O ] , [ D C B O ] − 1 = [ O B − 1 C − 1 − B − 1 D C − 1 ] 分块矩阵记忆 下面三个公式,可以类别矩阵乘法进行记忆
[ E r O − C A − 1 E n − r ] [ A B C D ] = [ A B O D − C A − 1 B ] \left[\begin{array}{cc}
E _r & O \\
- C A ^{-1} & E _{n-r}
\end{array}\right]\left[\begin{array}{ll}
A & B \\
C & D
\end{array}\right]=\left[\begin{array}{cc}
A & B \\
O & D - C A ^{-1} B
\end{array}\right] [ E r − C A − 1 O E n − r ] [ A C B D ] = [ A O B D − C A − 1 B ] 上面这个公式怎么记忆呢? 将第二个分块拒阵的第一行的 − C A − 1 - C A ^{-1} − C A − 1 C C C O O O
舒尔公式
分块矩阵的转置 [ A B C D ] T = [ A T C T B T D T ] \left[\begin{array}{ll}
A & B \\
C & D
\end{array}\right]^{T}=\left[\begin{array}{ll}
A ^{T} & C ^{T} \\
B ^{T} & D ^{T}
\end{array}\right] [ A C B D ] T = [ A T B T C T D T ]