38._矩阵乘法的应用_经济学_人口学和生态学应用 - 线性代数

经济学中的应用

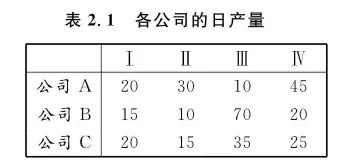
例某地区有三个公司： $\mathrm{A}, \mathrm{B}, \mathrm{C}$ ，每个公司都生产 I ，II，III，IV 四种产品．已知每个公司的日产量（单位：个）、每种产品的单价（元／个）和单位利润（元／个），见表2．1和表 2.2 ，求每个公司的总收入与总利润． $图片$

$图片$

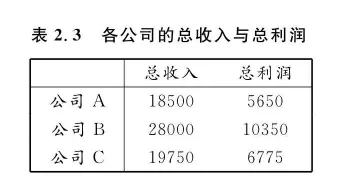
解：根据总收入等于总产量乘以产品单价，总利润等于产品总量乘以单位利润，可得表 2．3： $图片$

上面的三个数表可以用三个矩阵表示，设

\boldsymbol{A}=\left[\begin{array}{cccc} 20 & 30 & 10 & 45 \\ 15 & 10 & 70 & 20 \\ 20 & 15 & 35 & 25 \end{array}\right], \boldsymbol{B}=\left[\begin{array}{cc} 100 & 20 \\ 150 & 45 \\ 300 & 120 \\ 200 & 60 \end{array}\right], \boldsymbol{C}=\left[\begin{array}{cc} 18500 & 5650 \\ 28000 & 10350 \\ 19750 & 6775 \end{array}\right]

矩阵 $\boldsymbol{C}$ 是矩阵 $\boldsymbol{A}$ 与矩阵 $\boldsymbol{B}$ 的乘积，即 $\boldsymbol{C}=\boldsymbol{A} \boldsymbol{B}$ ．

其它学科的应用

生态学、经济学和工程学等许多领域中经常需要对随时间变化的动态系统进行数学建模。系统中的某些量按离散时间间隔测量，于是产生了向量序列 $\boldsymbol{x}_0, \boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_k$ 。其中的元素 $\boldsymbol{x}_k$ 给出了第 $k$ 次测量时系统状态的有关信息。

如果存在矩阵 $\boldsymbol{A}$ ，使得 $\boldsymbol{x}_1=\boldsymbol{A} \boldsymbol{x}_0, \boldsymbol{x}_2=\boldsymbol{A} x_1$ ，以此类推，

\boldsymbol{x}_{k+1}=\boldsymbol{A} \boldsymbol{x}_k, \quad k=0,1,2, \cdots ...(2.2.9)

则称（2．2．9）为一个线性差分方程（linear difference equation）或者递归方程（recurrence relation）。给定这样一个方程，如果已知 $\boldsymbol{x}_0$ ，则可以计算 $\boldsymbol{x}_1, \boldsymbol{x}_2$ 等。下面是一些实际问题中产生的差分方程。

一个婚姻状况计算的简单模型．

例某个城镇中，每年有 $30 \%$ 的已婚女性离婚， $20 \%$ 的单身女性结婚，城镇中有 8000位已婚女性和 2000 位单身女性。假设所有女性的总数为一常数，一年后，有多少已婚女性和单身女性呢？两年后呢？

解可用如下方式构造矩阵 $\boldsymbol{A}$ ．矩阵 $\boldsymbol{A}$ 的第一行元素分别为一年后处于婚姻状态的已婚女性和已婚的单身女性的百分比，第二行元素分别为一年后离婚的已婚女性和未婚的单身女性的百分比．因此

\boldsymbol{A}=\left[\begin{array}{ll} 0.70 & 0.20 \\ 0.30 & 0.80 \end{array}\right]

若令

\boldsymbol{x}=\left[\begin{array}{l} 8000 \\ 2000 \end{array}\right],

则一年后的已婚女性和单身女性人数可以用 $\boldsymbol{A}$ 乘以 $\boldsymbol{x}$ 计算，即

\boldsymbol{A} \boldsymbol{x}=\left[\begin{array}{ll} 0.70 & 0.20 \\ 0.30 & 0.80 \end{array}\right]\left[\begin{array}{l} 8000 \\ 2000 \end{array}\right]=\left[\begin{array}{l} 6000 \\ 4000 \end{array}\right]

一年后将有 6000 位已婚女性， 4000 位单身女性。要求两年后已婚女性和单身女性的数量，计算如下：

\boldsymbol{A}^2 \boldsymbol{x}=\boldsymbol{A}(\boldsymbol{A} \boldsymbol{x})=\left[\begin{array}{ll} 0.70 & 0.20 \\ 0.30 & 0.80 \end{array}\right]\left[\begin{array}{l} 6000 \\ 4000 \end{array}\right]=\left[\begin{array}{l} 5000 \\ 5000 \end{array}\right] .

两年后，一半的女性将为已婚，一半的女性将为单身．一般地， $n$ 年后已婚女性和单身女性的数量可由 $\boldsymbol{A}^n \boldsymbol{x}$ 求得．

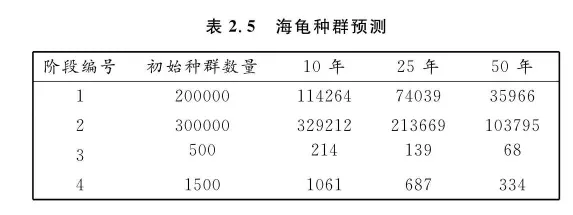
生态学：海龟的种群统计．

管理和保护大量野生物种依赖于人们模型化动物种群的能力。一个经典的模型化方法是将物种的生命周期划分为几个阶段。该模型假设每一阶段种群的大小仅依赖于雌性的数量，并且每一个雌性个体从一年到下一年存活的概率仅依赖于它在生命周期的阶段，而并不依赖于个体的实际年龄。例如，我们考虑一个 4 个阶段的模型来分析海龟的动态种群。

在每一个阶段，我们估计出一年中存活的概率，并用每年期望的产卵量近似给出繁殖能力的估计．这些结果在表 2.4 中给出．在每一阶段名称后的圆括号中给出该阶段近似的年龄． $图片$

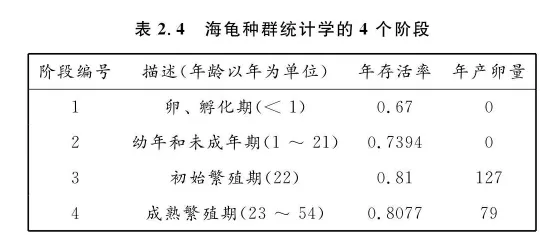
若 $d_i$ 表示第 $i$ 个阶段持续的时间， $s_i$ 为该阶段的存活率，那么在第 $i$ 阶段中，下一年仍然存活的比例将为

p_i=\left(\frac{1-s_i^{d_i-1}}{1-s_i^{d_i}}\right) s_i,

而下一年转移到第 $i+1$ 个阶段时，可以存活的比例应为

q_i=\frac{s_i^{d_i}\left(1-s_i\right)}{1-s_i^{d_i}} .

若令 $e_i$ 表示阶段 $i(i=2,3,4)$ 一年中平均的产卵量，并构造矩阵

\boldsymbol{L}=\left[\begin{array}{cccc} p_1 & e_2 & e_3 & e_4 \\ q_1 & p_2 & 0 & 0 \\ 0 & q_2 & p_2 & 0 \\ 0 & 0 & q_3 & p_3 \end{array}\right], ...(2.2.10)

则 $\boldsymbol{L}$ 可以用于预测以后每阶段海龟的数量．形如（2．2．10）的矩阵称为莱斯利（Leslie）矩阵，相应的种群模型通常称为莱斯利种群模型 ${ }^{(1)(2)}$ ．利用表2．4给出的数字，模型的莱斯利矩阵为

\boldsymbol{L}=\left[\begin{array}{cccc} 0 & 0 & 127 & 79 \\ 0.67 & 0.7394 & 0 & 0 \\ 0 & 0.0006 & 0 & 0 \\ 0 & 0 & 0.81 & 0.8077 \end{array}\right]

设初始时种群在各个阶段的数量分别为 $200000,300000,500$ 和 1500 ．若将这个初始种群数量表示为向量 $\boldsymbol{x}_0, 1$ 年后各个阶段的种群数量可如下计算：

\boldsymbol{x}_1=\boldsymbol{L} \boldsymbol{x}_0=\left[\begin{array}{cccc} 0 & 0 & 127 & 79 \\ 0.67 & 0.7394 & 0 & 0 \\ 0 & 0.0006 & 0 & 0 \\ 0 & 0 & 0.81 & 0.8077 \end{array}\right]\left[\begin{array}{c} 200000 \\ 300000 \\ 500 \\ 1500 \end{array}\right]=\left[\begin{array}{c} 182000 \\ 355820 \\ 180 \\ 1617 \end{array}\right]

（上述结果已经四舍五入到最近的整数）为求得 2 年后种群数量向量，再次左乘以矩阵 $\boldsymbol{L}$ ，即

\boldsymbol{x}_2=\boldsymbol{L} \boldsymbol{x}_1=\boldsymbol{L}^2 \boldsymbol{x}_0 \text {. }

一般地， $k$ 年后种群数量可以通过计算向量 $\boldsymbol{x}_k=\boldsymbol{L}^k \boldsymbol{x}_0$ 求得．为观察长时间的趋势，我们计算 $\boldsymbol{x}_{10}, \boldsymbol{x}_{25}, \boldsymbol{x}_{50}$ ，结果归纳在表2．5中．这个模型预测，繁殖期的海龟数量将在 50 年后减少 $80 \%$ 。

$图片$