1._矩阵重要公式汇总

矩阵的初等变换

性质1 一个非零常数乘矩阵的某一行 (列) 性质2 互换矩阵中某两行 (列) 的位置 性质3 矩阵的某一行 (列) 的 kk 倍加到另一行 (列)

矩阵转置性质

(AT)T=A\left(\boldsymbol{A}^{\mathrm{T}}\right)^{\mathrm{T}}=\boldsymbol{A}. (A+B)T=AT+BT(\boldsymbol{A}+\boldsymbol{B})^{\mathrm{T}}=\boldsymbol{A}^{\mathrm{T}}+\boldsymbol{B}^{\mathrm{T}}.

(λA)T=λAT(\lambda \boldsymbol{A})^{\mathrm{T}}=\lambda \boldsymbol{A}^{\mathrm{T}}.

(AB)T=BTAT(\boldsymbol{A} \boldsymbol{B})^{\mathrm{T}}=\boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}.

重要作用： ① 求解XA=CXA=C 方程，详见逆矩阵解方程 ② 判断对称矩阵，即(AT)=A\left(\boldsymbol{A}^{\mathrm{T}}\right)=\boldsymbol{A}.

伴随矩阵性质

伴随矩阵一般不满足 (A+B)∗≠A∗+B∗(\boldsymbol{A}+\boldsymbol{B})^* \neq \boldsymbol{A}^*+\boldsymbol{B}^*

AA∗=A∗A=∣A∣E\boldsymbol{A} \boldsymbol{A}^*=\boldsymbol{A}^* \boldsymbol{A}=|\boldsymbol{A}| \boldsymbol{E}..

(kA)∗=kn−1A∗(n≥2)(k \boldsymbol{A})^*=k^{n-1} \boldsymbol{A}^*(n \geq 2).

(AB)∗=B∗A∗(\boldsymbol{A B})^*=\boldsymbol{B}^* \boldsymbol{A}^*.

∣A∗∣=∣A∣n−1(n≥2)\left|\boldsymbol{A}^*\right|=|\boldsymbol{A}|^{n-1}(n \geq 2).

(A∗)−1=(A−1)∗=1∣A∣A\left(A^*\right)^{-1}=\left(A^{-1}\right)^*=\frac{1}{|A|} A.

(A∗)T=(AT)∗\left(\boldsymbol{A}^*\right)^{\mathrm{T}}=\left(\boldsymbol{A}^{\mathrm{T}}\right)^*.

(A∗)∗=∣A∣n−2A(n≥3)\left(\boldsymbol{A}^*\right)^*=|\boldsymbol{A}|^{n-2} \boldsymbol{A}(n \geq 3).

矩阵可逆与不可逆的充分必要条件

矩阵A可逆

所谓可逆，就是可倒(虽然我们从不这么叫，但是这样类比容易记忆)，即ax=bax=b里，aa有倒数，aa有倒数要求a≠0a\ne0, 你或者就把aa当做数字2看待，此时 2≠02 \ne 0, 22 可以变换为 11(即单位矩阵EE)，方程2x=b2x=b有唯一解（不管bb是否为零）,他是满秩，且秩为nn

①nn 阶矩阵 A\boldsymbol{A} 可逆 ⇔∣A∣≠0\Leftrightarrow|\boldsymbol{A}| \neq 0 ⇔AB=E(\Leftrightarrow A B=E( 或 BA=E\boldsymbol{B} \boldsymbol{A}=\boldsymbol{E} ） ⇔r(A)=n\Leftrightarrow \mathrm{r}(A)=n ⇔A∗\Leftrightarrow A^* 可逆 ⇔A\Leftrightarrow \boldsymbol{A} 可以表示为若干初等矩阵的乘积 ⇔A\Leftrightarrow \boldsymbol{A} 与 E\boldsymbol{E} 等价 ⇔Ax=0\Leftrightarrow \boldsymbol{A x}=\mathbf{0} 只有零解 ⇔∀b,Ax=b\Leftrightarrow \forall \boldsymbol{b}, \quad \boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 有唯一解 ⇔A\Leftrightarrow \boldsymbol{A} 的列（行）向量组线性无关 ⇔A\Leftrightarrow \boldsymbol{A} 的特征值都不为 0 .

矩阵AA不可逆

矩阵AA不可逆，就是0x=b0x=b，如果b=0b=0 就变成0x=00x=0他有非零解，如果，如果bb不等于零，就变成 0x=10x=1 方程组无解。

② nn 阶矩阵 A\boldsymbol{A} 不可逆 ⇔∣A∣=0\Leftrightarrow|\boldsymbol{A}|=0 ⇔r(A)<n\Leftrightarrow \mathrm{r}(\boldsymbol{A})< n ⇔Ax=0\Leftrightarrow A x=0 有非零解 ⇔A\Leftrightarrow \boldsymbol{A} 的列 (行) 向量组线性相关 ⇔0\Leftrightarrow 0 是 A\boldsymbol{A} 的特征值.

重要作用：判断方程组有没有解，典型例题 问 λ\lambda 取何值时，下面的齐次线性方程组有零解？有非零解？有无穷多解并求出其基础解系。

{λx1+x2+3x3=0x1+(λ−1)x2+x3=0x1+x2+(λ−1)x3=0\left\{\begin{array}{l} \lambda x_1+x_2+3 x_3=0 \\ x_1+(\lambda-1) x_2+x_3=0 \\ x_1+x_2+(\lambda-1) x_3=0 \end{array}\right.

可逆矩阵的性质

(1) 若 A\boldsymbol{A} 可逆, 则 A−1\boldsymbol{A}^{-1} 亦可逆, 且 (A−1)−1=A\left(\boldsymbol{A}^{-1}\right)^{-1}=\boldsymbol{A}. (2) 若 A\boldsymbol{A} 可逆, 则 kA(k≠0)k \boldsymbol{A}(k \neq 0) 亦可逆, 且 (kA)−1=1kA−1(k \boldsymbol{A})^{-1}=\frac{1}{k} \boldsymbol{A}^{-1}. (3) 若 A,B\boldsymbol{A}, \boldsymbol{B} 可逆, 则 ABA B 亦可逆, 且 (AB)−1=B−1A−1(A B)^{-1}=B^{-1} A^{-1}. (4) 若 A\boldsymbol{A} 可逆, 则 AT\boldsymbol{A}^{\mathrm{T}} 亦可逆, 且 (AT)−1=(A−1)T\left(\boldsymbol{A}^{\mathrm{T}}\right)^{-1}=\left(\boldsymbol{A}^{-1}\right)^{\mathrm{T}}. (5) ∣A−1∣=1∣A∣\left|\boldsymbol{A}^{-1}\right|=\dfrac{1}{|\boldsymbol{A}|}.

注：一般的(A+B)−1≠A−1+B−1(A+B)^{-1} \ne A^{-1}+B^{-1}

求逆的方法

(1) 定义法: 若 AB=E\boldsymbol{A B}=\boldsymbol{E}, 则 A−1=B\boldsymbol{A}^{-1}=\boldsymbol{B}.

(2) 伴随矩阵法: A−1=1∣A∣A∗\boldsymbol{A}^{-1}=\frac{1}{|\boldsymbol{A}|} \boldsymbol{A}^*. (3) 初等行变换法: (A:E)⟶⟶(E:A−1)(\boldsymbol{A}: \boldsymbol{E}) \stackrel{\stackrel{ }{\longrightarrow}}{\longrightarrow}\left(\boldsymbol{E}: \boldsymbol{A}^{-1}\right). (4) 分块矩阵求逆法: ①(AOOB)−1=(A−1OOB−1)\left(\begin{array}{cc}A & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{B}\end{array}\right)^{-1}=\left(\begin{array}{cc}A^{-1} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{B}^{-1}\end{array}\right). ② (OABO)−1=(OB−1A−1O)\left(\begin{array}{ll}\boldsymbol{O} & \boldsymbol{A} \\ \boldsymbol{B} & \boldsymbol{O}\end{array}\right)^{-1}=\left(\begin{array}{cc}\boldsymbol{O} & B^{-1} \\ A^{-1} & \boldsymbol{O}\end{array}\right).

逆矩阵教程

矩阵秩的性质

(1) 0≤r(Am×n)≤min⁡{m,n}0 \leq \mathrm{r}\left(\boldsymbol{A}_{m \times n}\right) \leq \min \{m, n\}. (2) r(A)=r(AT)=r(kA)=r(AAT)=r(ATA)(k≠0)\mathrm{r}(\boldsymbol{A})=\mathrm{r}\left(\boldsymbol{A}^{\mathrm{T}}\right)=\mathrm{r}(k \boldsymbol{A})=\mathrm{r}\left(\boldsymbol{A} \boldsymbol{A}^{\mathrm{T}}\right)=\mathrm{r}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)(k \neq 0). (3) r(A+B)≤r(A)+r(B)\mathrm{r}(\boldsymbol{A}+\boldsymbol{B}) \leq \mathrm{r}(\boldsymbol{A})+\mathrm{r}(\boldsymbol{B}). (4) max⁡{r(A),r(B)}≤r(A,B)≤r(A)+r(B)\max \{\mathrm{r}(\boldsymbol{A}), \mathrm{r}(\boldsymbol{B})\} \leq \mathrm{r}(\boldsymbol{A}, \boldsymbol{B}) \leq \mathrm{r}(\boldsymbol{A})+\mathrm{r}(\boldsymbol{B}). (5) r(AB)≤min⁡{r(A),r(B)}\mathrm{r}(A B) \leq \min \{\mathrm{r}(\boldsymbol{A}), \mathrm{r}(\boldsymbol{B})\}. (6) 若 A\boldsymbol{A} 可逆, 则 r(AB)=r(B),r(BA)=r(B)\mathrm{r}(\boldsymbol{A} \boldsymbol{B})=\mathrm{r}(\boldsymbol{B}), \mathrm{r}(\boldsymbol{B} \boldsymbol{A})=\mathrm{r}(\boldsymbol{B}). (7) 若 Am×nBn×s=O\boldsymbol{A}_{m \times n} \boldsymbol{B}_{n \times s}=\boldsymbol{O}, 则 r(A)+r(B)≤n\mathrm{r}(\boldsymbol{A})+\mathrm{r}(\boldsymbol{B}) \leq n ( A\boldsymbol{A} 的列数). (8) 设 A\boldsymbol{A} 是 nn 阶矩阵 (n≥2)(n \geq 2), 则 r(A∗)={n,r(A)=n,1,r(A)=n−1,0,r(A)<n−1.\mathrm{r}\left(\boldsymbol{A}^*\right)=\left\{\begin{array}{lc}n, & \mathrm{r}(\boldsymbol{A})=n, \\ 1, & \mathrm{r}(\boldsymbol{A})=n-1, \\ 0, & \mathrm{r}(\boldsymbol{A}) < n-1 .\end{array}\right. (9) 左乘列满秩矩阵 (右乘行满秩矩阵) 不改变矩阵的秩.

矩阵的性质主要在证明题里大量使用。

矩阵等价、相似与合同

图片

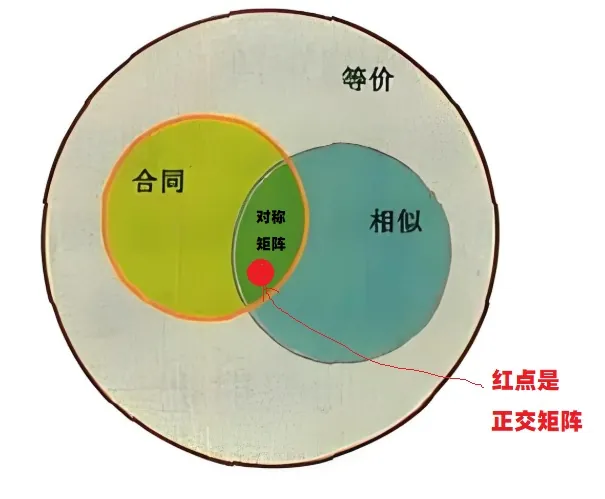
1.等价变换(初等变换) 若：PAQ=BP A Q=B（其中 PP 和 QQ 都是可逆矩阵），则称：矩阵 AA 和 BB 等价。

2.相似变换 若：P−1AP=BP^{-1} A P=B（其中 PP 是可逆矩阵），则称：矩阵 AA 和 BB 相似。

3.合同变换 若： P⊤AP=B\mathbf{P}^{\top} \mathbf{A P}=\mathbf{B}（其中 P\mathbf{P} 是可逆矩阵），则称：矩阵A和B合同。

4.正交变换 如果一个矩阵AA即满足相似变换又满足合同编号，那么他就是正交变换。即如果 ATA=EA^T A=E 则 AA是正交矩阵。

重要结论：

若矩阵A和B等价，则矩阵秩不变，即初等变换不改变矩阵的秩 若矩阵A和B相似，则A和B有相同的特征值。即相似变换特征值不变 若矩阵A和B合同，则A和B有相同的正、负惯性指数.合同变换惯性指数不变

左行右列定理

在矩阵 A\boldsymbol{A} 的左边乘初等矩阵 P\boldsymbol{P}, 相当于进行了一次初等行变换;

在矩阵 A\boldsymbol{A}的右边乘初等矩阵 P\boldsymbol{P}, 相当于进行了一次初等列变换

用初等矩阵知识求 P1mAP2n \boldsymbol{P}_1^m \boldsymbol{A} \boldsymbol{P}_2^n

用初等矩阵知识求 P1mAP2n\boldsymbol{P}_1^m \boldsymbol{A} \boldsymbol{P}_2^n 若 P1,P2\boldsymbol{P}_1, \boldsymbol{P}_2 均为初等矩阵, m,nm, n 为正整数, 则 P1mAP2n\boldsymbol{P}_1^m \boldsymbol{A} \boldsymbol{P}_2^n 表示先对 A\boldsymbol{A} 作了与 P1\boldsymbol{P}_1 相同的初等行变换, 且重复 mm 次; 再对 P1mA\boldsymbol{P}_1^m \boldsymbol{A} 作了与 P2\boldsymbol{P}_2 相同的初等列变换, 且重复 nn 次

用相似理论求 An\boldsymbol{A}^n

(1)若 A∼B\boldsymbol{A} \sim \boldsymbol{B}, 则 A=PBP−1,An=PBnP−1\boldsymbol{A}=\boldsymbol{P} \boldsymbol{B} \boldsymbol{P}^{-1}, \boldsymbol{A}^n=\boldsymbol{P B}^n \boldsymbol{P}^{-1} (2)若 A∼Λ\boldsymbol{A} \sim \boldsymbol{\Lambda}, 则 A=PΛP−1,An=PnP−1\boldsymbol{A}=\boldsymbol{P} \boldsymbol{\Lambda} \boldsymbol{P}^{-1}, \boldsymbol{A}^n=\boldsymbol{P}^n \boldsymbol{P}^{-1}

要求AnA^n A\boldsymbol{A} 为方阵且 r(A)=1r(\boldsymbol{A})=1 则An=[tr⁡(A)]n−1A\boldsymbol{A}^n=[\operatorname{tr}(\boldsymbol{A})]^{n-1} \boldsymbol{A}

试算 A2\boldsymbol{A}^2 (或 A3\boldsymbol{A}^3 ), 找规律 (1)若 A2=kA\boldsymbol{A}^2=k \boldsymbol{A}, 则 An=kn−1A\boldsymbol{A}^n=k^{n-1} \boldsymbol{A} (2)若 A2=kE\boldsymbol{A}^2=k \boldsymbol{E}, 则 {A2n=knEA2n+1=knA\left\{\begin{array}{l}\boldsymbol{A}^{2 n}=k^n \boldsymbol{E} \\ \boldsymbol{A}^{2 n+1}=k^n \boldsymbol{A}\end{array}\right.

分块矩阵的性质

分块矩阵的性质和普通矩阵的性质基本上是一致的，比如一个2×22\times2普通矩阵，完全可以看成4个分块矩阵。

（1）转置：[ABCD]T=[ATCTBTDT]\left[\begin{array}{ll}\boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{D}\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{ll}\boldsymbol{A}^{\mathrm{T}} & \boldsymbol{C}^{\mathrm{T}} \\ \boldsymbol{B}^{\mathrm{T}} & \boldsymbol{D}^{\mathrm{T}}\end{array}\right] （2）加法：[A1A2A3A4]+[B1B2B3B4]=[A1+B1A2+B2A3+B3A4+B4]\left[\begin{array}{ll}\boldsymbol{A}_1 & \boldsymbol{A}_2 \\ \boldsymbol{A}_3 & \boldsymbol{A}_4\end{array}\right]+\left[\begin{array}{ll}\boldsymbol{B}_1 & \boldsymbol{B}_2 \\ \boldsymbol{B}_3 & \boldsymbol{B}_4\end{array}\right]=\left[\begin{array}{ll}\boldsymbol{A}_1+\boldsymbol{B}_1 & \boldsymbol{A}_2+\boldsymbol{B}_2 \\ \boldsymbol{A}_3+\boldsymbol{B}_3 & \boldsymbol{A}_4+\boldsymbol{B}_4\end{array}\right] （3）数乘：k[ABCD]=[kAkBkCkD]k\left[\begin{array}{ll}\boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{D}\end{array}\right]=\left[\begin{array}{ll}\boldsymbol{k} \boldsymbol{A} & \boldsymbol{k} \boldsymbol{B} \\ \boldsymbol{k} \boldsymbol{C} & \boldsymbol{k} \boldsymbol{D}\end{array}\right] （4） 乘法：[ABCD][XYZW]=[AX+BZAY+BWCX+DZCY+DW]\left[\begin{array}{ll}\boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{D}\end{array}\right]\left[\begin{array}{cc}\boldsymbol{X} & \boldsymbol{Y} \\ \boldsymbol{Z} & \boldsymbol{W}\end{array}\right]=\left[\begin{array}{ll}\boldsymbol{A} \boldsymbol{X}+\boldsymbol{B} \boldsymbol{Z} & \boldsymbol{A} \boldsymbol{Y}+\boldsymbol{B} \boldsymbol{W} \\ \boldsymbol{C} \boldsymbol{X}+\boldsymbol{D} \boldsymbol{Z} & \boldsymbol{C} \boldsymbol{Y}+\boldsymbol{D} \boldsymbol{W}\end{array}\right] （5）若 A,BA, B 分别为 m,nm, n 阶方阵，则分块对角矩阵的幂为 [AOOB]k=[AkOOBk]\left[\begin{array}{ll}A & O \\ O & B\end{array}\right]^k=\left[\begin{array}{ll}A^k & O \\ O & B^k\end{array}\right]

四个小公式

考试分块矩阵最爱考的是个小公式，自己可以推一下,经常作为期末考试选择题出

[BODC]−1=[B−1O−C−1DB−1C−1],[BDOC]−1=[B−1−B−1DC−1OC−1],[OBCD]−1=[−C−1DB−1C−1B−1O],[DBCO]−1=[OC−1B−1−B−1DC−1]\begin{aligned} & {\left[\begin{array}{ll} \boldsymbol{B} & \boldsymbol{O} \\ \boldsymbol{D} & \boldsymbol{C} \end{array}\right]^{-1}=\left[\begin{array}{cc} \boldsymbol{B}^{-1} & \boldsymbol{O} \\ -\boldsymbol{C}^{-1} \boldsymbol{D} \boldsymbol{B}^{-1} & \boldsymbol{C}^{-1} \end{array}\right],\left[\begin{array}{ll} \boldsymbol{B} & \boldsymbol{D} \\ \boldsymbol{O} & \boldsymbol{C} \end{array}\right]^{-1}=\left[\begin{array}{cc} \boldsymbol{B}^{-1} & -\boldsymbol{B}^{-1} \boldsymbol{D} \boldsymbol{C}^{-1} \\ \boldsymbol{O} & \boldsymbol{C}^{-1} \end{array}\right],} \\ & {\left[\begin{array}{ll} \boldsymbol{O} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{D} \end{array}\right]^{-1}=\left[\begin{array}{cc} -\boldsymbol{C}^{-1} \boldsymbol{D} \boldsymbol{B}^{-1} & \boldsymbol{C}^{-1} \\ \boldsymbol{B}^{-1} & \boldsymbol{O} \end{array}\right],\left[\begin{array}{ll} \boldsymbol{D} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{O} \end{array}\right]^{-1}=\left[\begin{array}{cc} \boldsymbol{O} & \boldsymbol{C}^{-1} \\ \boldsymbol{B}^{-1} & -\boldsymbol{B}^{-1} \boldsymbol{D} \boldsymbol{C}^{-1} \end{array}\right]} \end{aligned}

分块矩阵的逆

主对角矩阵的逆为各个元素的逆。

若A=[A1A2⋱As]若 \boldsymbol{A}=\left[\begin{array}{llll} \boldsymbol{A}_1 & & & \\ & \boldsymbol{A}_2 & & \\ & & \ddots & \\ & & & \boldsymbol{A}_s \end{array}\right]
则A−1=[A1−1A2−1⋱As−1]则 \boldsymbol{A}^{-1}=\left[\begin{array}{llll} \boldsymbol{A}_1^{-1} & & & \\ & \boldsymbol{A}_2^{-1} & & \\ & & \ddots & \\ & & & \boldsymbol{A}_s^{-1} \end{array}\right]

主对角矩阵的逆为各个元素的逆，然后倒着排列。

若A=[A1A2⋱As]若 A=\left[\begin{array}{llll} & & & A_1 \\ & & A_2 & \\ & \ddots & & \\ A_s & & & \end{array}\right]
则A−1=[As−1.A2−1A1−1]则 A^{-1}=\left[\begin{array}{llll} & & & A_s^{-1} \\ & & . & \\ & A_2^{-1} & & \\ A_1^{-1} & & & \end{array}\right]
前の章2矩阵
次の章2._矩阵的定义