36._奇异值分解_SVD_介绍和可视化理解

介绍

终于有机会来介绍我在线性代数中最喜欢的技术——奇异值分解 （SVD），从某种程度上来说，这可能是线性代数中最具有理论意义和实用价值的技术了，虽然很遗憾我在本科毕业后大概两年才理解到这一点，这种技术可以对任何矩阵适用，不仅仅是方阵，对一般的矩形矩阵也是适用的，仅以我的知识层面而言，SVD的应用就包括，例如推荐系统中的协同滤波和图像处理领域的图像压缩。我们在这期推送中，有机会向大家介绍这种技术，好了，让我们开始吧。

奇异值分解 （$SVD$）

首先，什么是$SVD$，你如何表示它？在数学中，我们可以将任何一个矩阵A做奇异值分解，用数学符号表示如下

这里：

1． $U$ 是一个 $n \times n$ 正交矩阵，其列叫做 $A$ 的左奇异向量。 2． $V$ 是一个$d \times d$ 正交矩阵，其列叫做 $A$ 的右奇异向量。 3． $S$ 是一个 $n \times d$ 对角矩阵，对角线上具有非负数字，我们通常将这些数字从大到小排序，人们给这些数字一个名称叫做 $A$ 的奇异值。

为了更清楚地介绍上面的名词，我们说如果存在满足下面公式的向量 $u$ 和 $v$ ，则向量 $u$ 和 $v$ 称为奇异向量。 $\sigma$ 叫做是一个奇异值。

我们要仔细观察一下方程（1）和方程（2），事实上他们表达的是同一个意思，我们注意到因为 $v$是正交矩阵，所以它的逆矩阵就是其转置矩阵，注意到这一点，我们就知道了方程（1）事实就是（2）的紧凑的矩阵形式，因此，每个奇异向量都有一个对应的奇异值。下面我们来进行可视化，颜色相同的列表示对应的奇异值和向量，如下图所示。

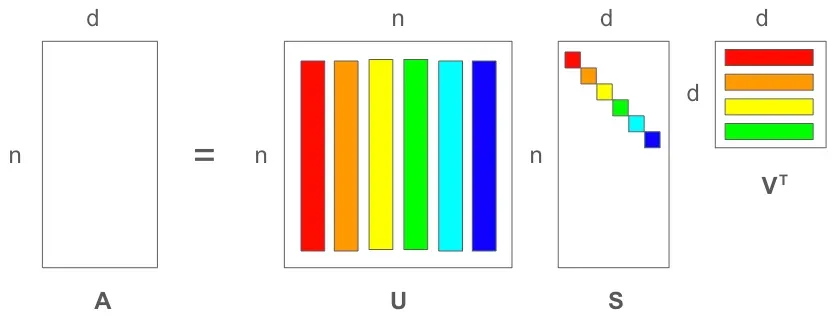
SVD和正交对角化的区别

到目前为止，我们有了$SVD$的初步概念，那么，在下一步，一个很自然的问题就是我们如何计算$SVD$？在深入研究这个问题之前，我想澄清另外一个问题即 $SVD$ 和大家熟知正交对角化之间的区别，因为它们是非常相似的概念。如果你已经忘了什么是正交对角化，那么我们还是首先回顾一下正交对角化的定义：参考附录2

1． $P$ 是 $A$ 的正交矩阵和正交特征向量

2． $D$ 是一个对角矩阵，其对角线上是 $A$ 的特征值。

SVD 和正交对角化之间的关键区别在于正交对角化仅适用于方阵。此外，虽然 SVD 在公式中有两个不同的矩阵（$U$ 和 $V$ ），但正交对角化只有一个矩阵（$P$ ）。这些公式究竟是什么意思？我们不妨做一些可视化的展示，帮助你理解这些矩阵。

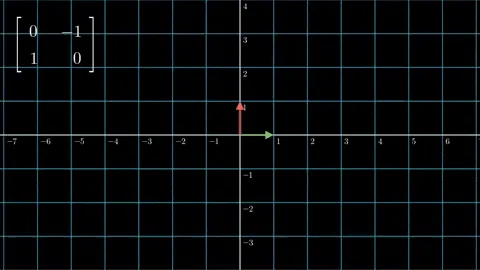
正交矩阵 — 旋转空间

对角矩阵 — 缩放空间

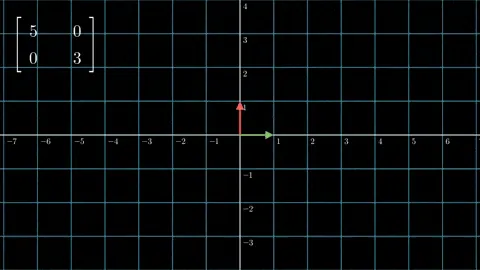
从上面两张动画中我们了解到了正交矩阵和对角矩阵的重要含义。正交矩阵总是使空间旋转或反射，而对角矩阵总是使空间缩放。我相信大家从动图中清楚地看到了这一点，为了防止你忘记这一点，我们在下面的图片中做了总结

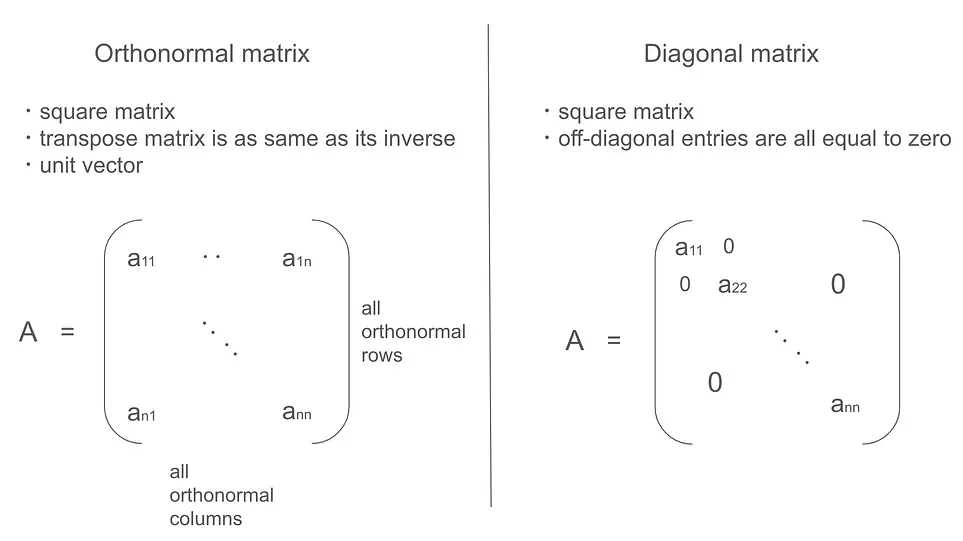
此外，还记得吗？我们提到过正交矩阵的转置矩阵等价于其逆矩阵。我们也可以通过可视化的方法来看出你可以看到，当你将正交矩阵应用于箭头时，箭头会旋转。然后，通过应用其转置矩阵，箭头返回到其原始坐标。因为它返回到原始坐标，所以它具有与逆矩阵相同的功能。

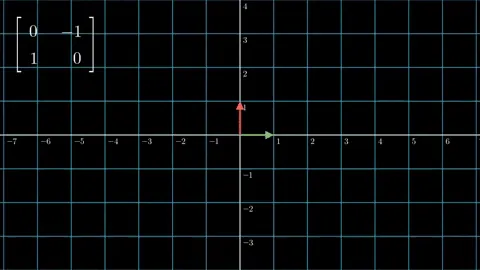
我们现在对正交矩阵和对角线矩阵的几何含义有了初步的了解，因此下面这张图可能会对我们有所启发。

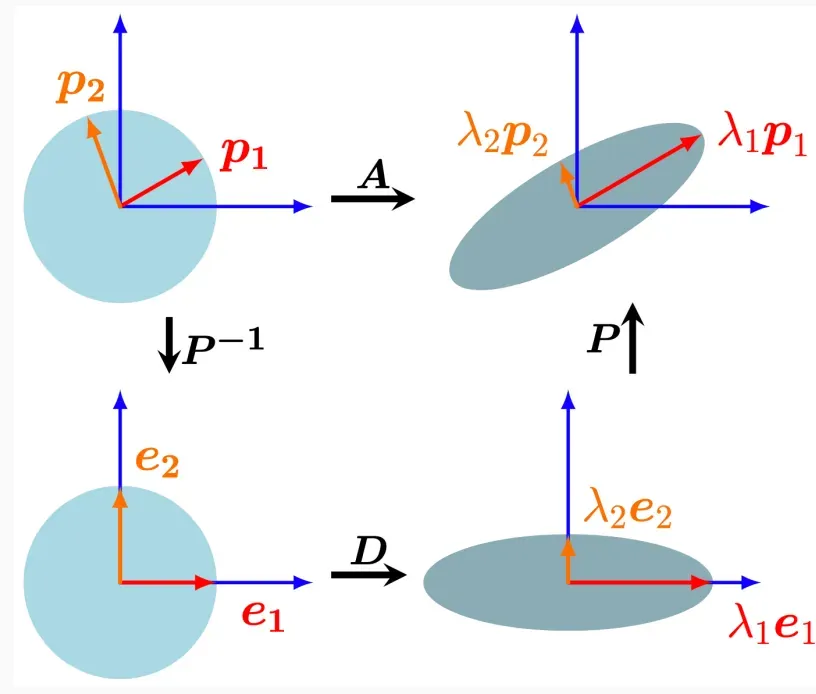
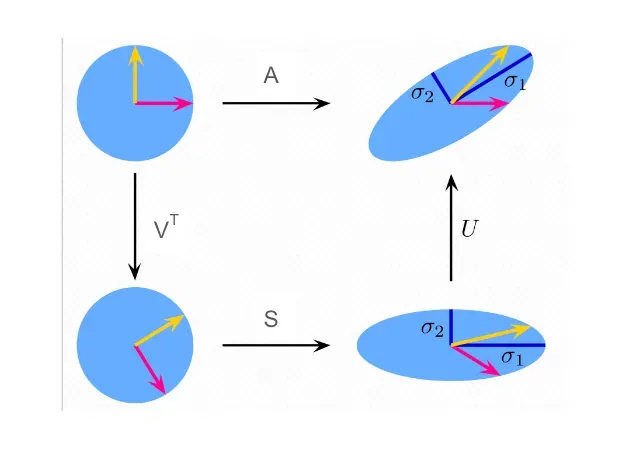
上图描述了正交对角化。下面那张图则表示SVD分解

如何计算 SVD

在实际算法中，我们可以计算 A 的 SVD，如下所示（＊表示转置共轭或者伴随）由于大多数的应用都是实矩阵，所以共轭就变得可有可无，因而在实矩阵的意义下，这个符号就是转置的意思。

1．计算左奇异向量（U）。它等于 $AA ^*$ 的特征向量。 2．计算右奇异向量（V）。它等于 $A^* A$ 的特征向量。 3．计算 $A A^*$ 或 $A^* A(D)$ 的特征值的平方根。

然后，我们就会得到 SVD 的所有信息。让我们验证此过程是否正确。例如，我将使用下面的矩阵：

第一步，您需要计算 $AA*$ 的特征向量。 下一步，您需要计算 $A*A$ 的特征向量。你可以用同样的方式证明 它。 对于最后一步，你必须计算来自 AA* 或 A*A 的特征值的平方根。而这两个具有相同的特征值！

虽然我们经历了 SVD 的数学过程，但实际上Python 里可以快速计算它，因为人们已经把相应的数学过程压缩到包里了，从而你可以方便的调用它们。

注：本文转载自微信公众号 MathSpark