17._雅可比行列式与雅可比矩阵及其意义
雅可比行列式(微分观点)
在 二阶行列式 里介绍过,行列式的值代表矩阵向量张成的空间体积。
线性函数
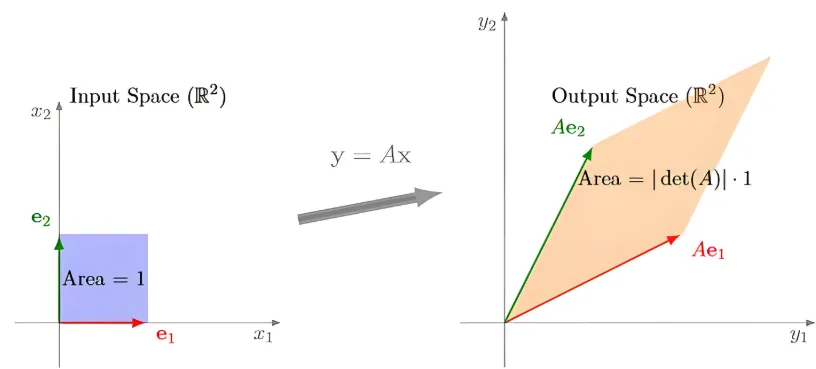
考虑一个由矩阵 定义的线性变换 ,其中 .这个变换将输入空间中的一个区域映射到输出空间中的另一个区域.矩阵 的行列式的绝对值 所衡量的正是这个变换对体积的缩放比例.
也就是说,如果输入空间中有一个体积为 的区域,经过变换后,其在输出空间中的对应区域的体积将是 .行列式的正负号则反映了变换是否保持了空间的"方向性"。
下图显示了在输入空间里的“体积”经过矩阵作用后,变成了在新空间里的“体积”。
 {width=500px}
{width=500px}
非线性函数
然而,现实世界中的多数变换并不是线性的.考虑一个一般的、可微的函数 ,其中 .这样的函数描述了一个非线性的空间扭曲.我们不能再用一个单一的矩阵来描述整个空间的体积变化,因为在空间的不同位置,扭曲的程度可能完全不同.这正是微分学的思想介入之处:考察局部的、无限小的尺度上的行为.
在一个特定的点 附近,任何一个光滑的非线性函数 都可以被一个线性函数来近似。具体而言,当我们从点 移动一个无限小的位移向量 到达点 时,函数值 的变化可以用泰勒展开来描述,其一阶近似为 .这里, 就是函数 在点 的雅可比矩阵 .
这个关系式是理解雅可比矩阵本质的关键。它表明,在点 的一个无限小的邻域内,复杂的非线性变换 的行为,可以被一个简单的线性变换所取代,而这个线性变换的矩阵正是雅可比矩阵 .换言之,雅可比矩阵是原非线性函数在某一点上的"最佳线性近似".它捕捉了在这一点附近,空间是如何被拉伸、压缩、旋转和剪切的。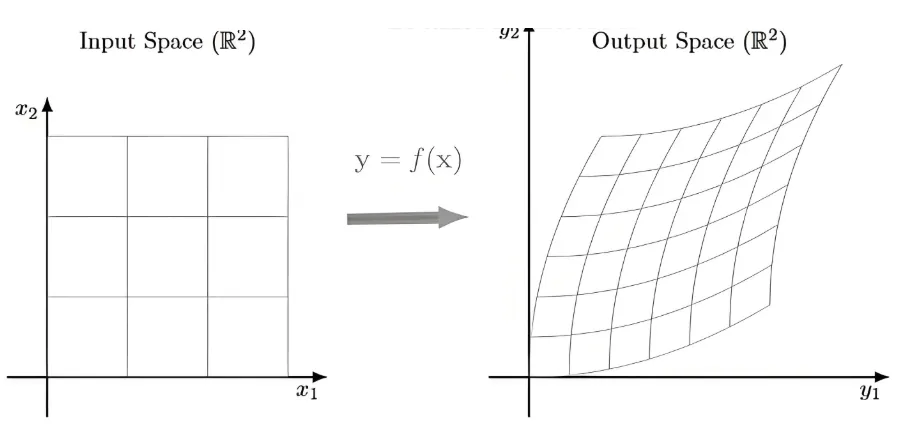 {width=500px}
{width=500px}
既然雅可比矩阵 扮演了在点 处的局部线性变换的角色,那么它的行列式 的意义也就随之明确了.结合我们最初对线性变换的理解,雅可比行列式 + 正是该变换在点 处对体积的"局部缩放率"。
通俗解读雅可比行列式
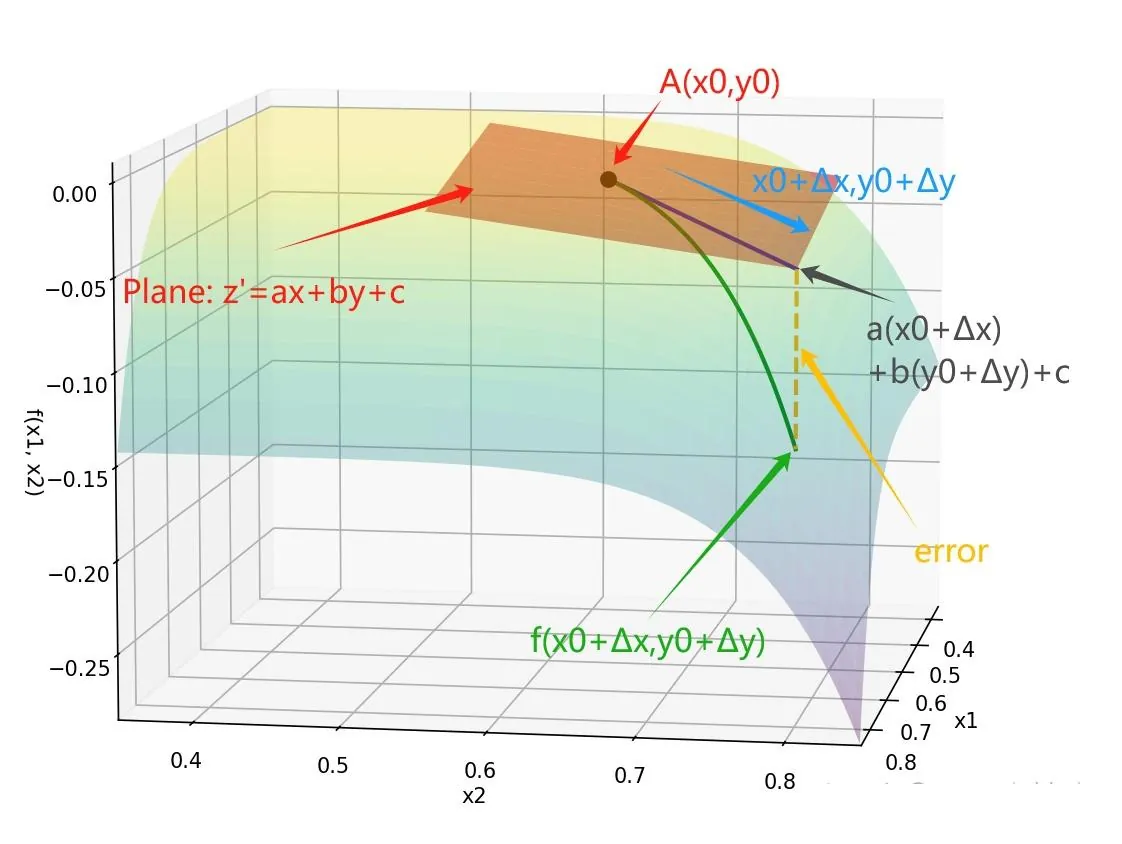
在全微分里 我们说过,全微分的本质使用 切平面的增量替代曲面的增量。
下面列出相关教程
(1)高等数学 https://kb.kmath.cn/kbase/detail.aspx?id=389
(2)数学分析里雅可比行列式 https://kb.kmath.cn/kbase/detail.aspx?id=2297
(3)复变函数里的雅可比行列式 https://kb.kmath.cn/kbase/detail.aspx?id=901