向量空间的基、维数与坐标 一句话就可以说明白:要测量空间里的一个点,需要有一个尺子,这个尺子就是坐标系,也就是“基”,这个点有一个值,就是坐标值,而组成基的向量个数就是维数,记作 dim V
定义1 在线性空间 V V V n n n α 1 , α 2 , ⋯ , α n \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n α 1 , α 2 , ⋯ , α n α 1 , α 2 , ⋯ , α n \alpha_1, \alpha_2, \cdots, \alpha_n α 1 , α 2 , ⋯ , α n v v v α \alpha α α 1 , α 2 , ⋯ , α n \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n α 1 , α 2 , ⋯ , α n α 1 , α 2 , ⋯ , α n \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n α 1 , α 2 , ⋯ , α n V V V 基 , n n n V V V 维数 ,记作 dim V = n \operatorname{dim} V=n dim V = n
只含一个零元素的线性空间称为零空间,零空间没有基,规定它的维数为 0 0 0 n n n V V V V n V_n V n n n n V n V_n V n α 1 , α 2 , ⋯ , α n \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n α 1 , α 2 , ⋯ , α n V n V_n V n V n V_n V n α 1 , α 2 , ⋯ , α n \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n α 1 , α 2 , ⋯ , α n
V n = { α = x 1 α 1 + x 2 α 2 + ⋯ + x n α n ∣ x 1 , x 2 , ⋯ , x n ∈ □ } , V_n=\left\{\boldsymbol{\alpha}=x_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+\cdots+x_n \boldsymbol{\alpha}_n \mid x_1, x_2, \cdots, x_n \in \square\right\}, V n = { α = x 1 α 1 + x 2 α 2 + ⋯ + x n α n ∣ x 1 , x 2 , ⋯ , x n ∈ □ } , 这就较清楚地显示出线性空间 V n V_n V n
例向量组 e 1 = ( 1 0 ⋮ 0 ) , e 2 = ( 0 1 ⋮ 0 ) , ⋯ , e n = ( 0 0 ⋮ 1 ) e _1=\left(\begin{array}{c}1 \\ 0 \\ \vdots \\ 0\end{array}\right), e _2=\left(\begin{array}{c}0 \\ 1 \\ \vdots \\ 0\end{array}\right), \cdots, e _n=\left(\begin{array}{c}0 \\ 0 \\ \vdots \\ 1\end{array}\right) \quad e 1 = 1 0 ⋮ 0 , e 2 = 0 1 ⋮ 0 , ⋯ , e n = 0 0 ⋮ 1 R n R ^n R n
如果 n n n A x = 0 A x =0 A x = 0 R ( A ) = r R(A)=r R ( A ) = r ξ 1 , ξ 2 , ⋯ , ξ n − r \xi_1, \xi_2, \cdots, \xi_{n-r} ξ 1 , ξ 2 , ⋯ , ξ n − r ξ 1 , ξ 2 , ⋯ , ξ n − r \xi_1, \xi_2, \cdots, \xi_{n-r} ξ 1 , ξ 2 , ⋯ , ξ n − r S S S S S S dim ( S ) = n − r = n − R ( A ) \operatorname{dim}(S)=n-r=n-R( A ) dim ( S ) = n − r = n − R ( A )
向量空间
L ( α 1 , α 2 , ⋯ , α s ) = { α = k 1 α 1 + k 2 α 2 + ⋯ + k s α s ∣ k 1 , k 2 , ⋯ , k s ∈ R } L \left( \alpha _1, \alpha _2, \cdots, \alpha _s\right)=\left\{ \alpha =k_1 \alpha _1+k_2 \alpha _2+\cdots+k_s \alpha _s \mid k_1, k_2, \cdots, k_s \in R \right\} L ( α 1 , α 2 , ⋯ , α s ) = { α = k 1 α 1 + k 2 α 2 + ⋯ + k s α s ∣ k 1 , k 2 , ⋯ , k s ∈ R } α 1 , α 2 , ⋯ , α s \alpha _1, \alpha _2, \cdots, \alpha _s α 1 , α 2 , ⋯ , α s 因此向量组 α 1 , α 2 , ⋯ , α s \alpha _1, \alpha _2, \cdots, \alpha _s α 1 , α 2 , ⋯ , α s L ( α 1 , α 2 , ⋯ , α s ) L \left( \alpha _1, \alpha _2, \cdots, \alpha _s\right) L ( α 1 , α 2 , ⋯ , α s )
向量组 α 1 , α 2 , ⋯ , α s \alpha _1, \alpha _2, \cdots, \alpha _s α 1 , α 2 , ⋯ , α s L ( α 1 , α 2 , ⋯ , α s ) L \left( \alpha _1, \alpha _2, \cdots, \alpha _s\right) L ( α 1 , α 2 , ⋯ , α s )
命题1 如果 α 1 , α 2 , ⋯ , α r \alpha_1, \alpha_2, \cdots, \alpha_r α 1 , α 2 , ⋯ , α r V V V V V V β \beta β α 1 , α 2 , ⋯ , α r \alpha_1, \alpha_2, \cdots, \alpha_r α 1 , α 2 , ⋯ , α r V V V β \beta β α 1 , α 2 , ⋯ , α r \alpha_1, \alpha_2, \cdots, \alpha_r α 1 , α 2 , ⋯ , α r λ 1 , λ 2 , ⋯ , λ r \lambda_1, \lambda_2, \cdots, \lambda_r λ 1 , λ 2 , ⋯ , λ r μ 1 , μ 2 , ⋯ , μ r \mu_1, \mu_2, \cdots, \mu_r μ 1 , μ 2 , ⋯ , μ r β = λ 1 α 1 + λ 2 α 2 + ⋯ + λ r α \boldsymbol{\beta}=\lambda_1 \boldsymbol{\alpha}_1+\lambda_2 \boldsymbol{\alpha}_2+\cdots+\lambda_r \boldsymbol{\alpha} β = λ 1 α 1 + λ 2 α 2 + ⋯ + λ r α β = μ 1 α 1 + μ 2 α 2 + ⋯ + μ r α r \boldsymbol{\beta}=\mu_1 \boldsymbol{\alpha}_1+\mu_2 \boldsymbol{\alpha}_2+\cdots+\mu_r \boldsymbol{\alpha}_r β = μ 1 α 1 + μ 2 α 2 + ⋯ + μ r α r 0 = ( λ 1 − μ 1 ) α 1 + ( λ 2 − μ 2 ) α 2 + ⋯ + ( λ r − μ r ) α r \quad \mathbf{0}=\left(\lambda_1-\mu_1\right) \boldsymbol{\alpha}_1+\left(\lambda_2-\mu_2\right) \boldsymbol{\alpha}_2+\cdots+\left(\lambda_r-\mu_r\right) \boldsymbol{\alpha}_r 0 = ( λ 1 − μ 1 ) α 1 + ( λ 2 − μ 2 ) α 2 + ⋯ + ( λ r − μ r ) α r α 1 , α 2 , ⋯ , α r \alpha_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_r α 1 , α 2 , ⋯ , α r λ 1 = μ 1 , λ 2 = μ 2 , ⋯ , λ r = μ r \lambda_1=\mu_1, \lambda_2=\mu_2, \cdots, \lambda_r=\mu_r λ 1 = μ 1 , λ 2 = μ 2 , ⋯ , λ r = μ r β \beta β α 1 , α 2 , ⋯ , α r \alpha_1, \alpha_2, \cdots, \alpha_r α 1 , α 2 , ⋯ , α r
坐标的定义 设 α , α 2 , ⋯ , α \alpha, \alpha_2, \cdots, \alpha α , α 2 , ⋯ , α V V V V V V β \beta β
β = λ 1 α 1 + λ 2 α 2 + ⋯ + λ r α , \boldsymbol{\beta}=\lambda_1 \boldsymbol{\alpha}_1+\lambda_2 \boldsymbol{\alpha}_2+\cdots+\lambda_r \boldsymbol{\alpha}, β = λ 1 α 1 + λ 2 α 2 + ⋯ + λ r α , 则称常数 λ 1 , λ 2 , ⋯ , λ r \lambda_1, \lambda_2, \cdots, \lambda_r λ 1 , λ 2 , ⋯ , λ r β \beta β α 1 , α 2 , ⋯ , α r \alpha_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_r α 1 , α 2 , ⋯ , α r R n \mathbf{R}^n R n e 1 , e 2 , ⋯ , e n e_1, e_2, \cdots, e_n e 1 , e 2 , ⋯ , e n R n \mathbf{R}^n R n
α = ( a 1 a 2 ⋮ a n ) \boldsymbol{\alpha}=\left(\begin{array}{c}
a_1 \\
a_2 \\
\vdots \\
a_n
\end{array}\right) α = a 1 a 2 ⋮ a n 在基 e 1 , e 2 , ⋯ , e n \boldsymbol{e}_1, \boldsymbol{e}_2, \cdots, \boldsymbol{e}_n e 1 , e 2 , ⋯ , e n α \boldsymbol{\alpha} α n n n a 1 , a 2 , ⋯ , a n a_1, a_2, \cdots, a_n a 1 , a 2 , ⋯ , a n
映射与变换 定义 设 V V V V ′ V^{\prime} V ′ F F F V V V V ′ V^{\prime} V ′ σ \sigma σ σ ( α + β ) = σ ( α ) + σ ( β ) , ∀ α , β ∈ V \sigma(\boldsymbol{\alpha}+\boldsymbol{\beta})=\sigma(\boldsymbol{\alpha})+\sigma(\boldsymbol{\beta}), \quad \forall \boldsymbol{\alpha}, \boldsymbol{\beta} \in V σ ( α + β ) = σ ( α ) + σ ( β ) , ∀ α , β ∈ V σ ( k α ) = k σ ( α ) , ∀ α ∈ V , ∀ k ∈ F \sigma(k \boldsymbol{\alpha})=k \sigma(\boldsymbol{\alpha}), \quad \forall \boldsymbol{\alpha} \in V, \quad \forall k \in F σ ( k α ) = kσ ( α ) , ∀ α ∈ V , ∀ k ∈ F σ \sigma σ V V V V ′ V^{\prime} V ′ V V V V ′ V^{\prime} V ′
简单的说:同纬度是变换,不同维度是映射。 比如二维平面上圆变成椭圆称之为变换。三维空间的球投影到二维平面上是映射。
例 在线性空间 F [ x ] n F[x]_n F [ x ] n
p 1 ( x ) = 1 , p 2 ( x ) = x , p 3 ( x ) = x 2 , ⋯ , p n ( x ) = x n − 1 p_1(x)=1, p_2(x)=x, p_3(x)=x^2, \cdots, p_n(x)=x^{n-1} p 1 ( x ) = 1 , p 2 ( x ) = x , p 3 ( x ) = x 2 , ⋯ , p n ( x ) = x n − 1 显然,p 1 ( x ) , p 2 ( x ) , p 3 ( x ) , ⋯ , p n ( x ) p_1(x), p_2(x), p_3(x), \cdots, p_n(x) p 1 ( x ) , p 2 ( x ) , p 3 ( x ) , ⋯ , p n ( x ) F [ x ] n F[x]_n F [ x ] n
f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + ⋯ + a n − 1 x n − 1 f(x)=a_0+a_1 x+a_2 x^2+a_3 x^3+\cdots+a_{n-1} x^{n-1} f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + ⋯ + a n − 1 x n − 1 可表示为 p 1 ( x ) , p 2 ( x ) , ⋯ , p n ( x ) p_1(x), p_2(x), \cdots, p_n(x) p 1 ( x ) , p 2 ( x ) , ⋯ , p n ( x )
f ( x ) = a 0 p 1 ( x ) + a 1 p 2 ( x ) + a 2 p 3 ( x ) + ⋯ + a n − 1 p n ( x ) f(x)=a_0 p_1(x)+a_1 p_2(x)+a_2 p_3(x)+\cdots+a_{n-1} p_n(x) f ( x ) = a 0 p 1 ( x ) + a 1 p 2 ( x ) + a 2 p 3 ( x ) + ⋯ + a n − 1 p n ( x ) 因此,F [ x ] n F[x]_n F [ x ] n n n n p 1 ( x ) , p 2 ( x ) , p 3 ( x ) , ⋯ , p n ( x ) p_1(x), p_2(x), p_3(x), \cdots, p_n(x) p 1 ( x ) , p 2 ( x ) , p 3 ( x ) , ⋯ , p n ( x ) f ( x ) f(x) f ( x ) p 1 ( x ) , p 2 ( x ) , p 3 ( x ) , ⋯ , p n ( x ) p_1(x), p_2(x), p_3(x), \cdots, p_n(x) p 1 ( x ) , p 2 ( x ) , p 3 ( x ) , ⋯ , p n ( x )
( a 0 a 1 ⋮ a n − 1 ) \left(\begin{array}{c}
a_0 \\
a_1 \\
\vdots \\
a_{n-1}
\end{array}\right) a 0 a 1 ⋮ a n − 1 例 验证 α 1 = ( 1 0 1 ) , α 2 = ( 2 1 − 1 ) α 3 = ( − 1 1 − 3 ) \alpha _1=\left(\begin{array}{c}1 \\ 0 \\ 1\end{array}\right), \alpha _2=\left(\begin{array}{c}2 \\ 1 \\ -1\end{array}\right) \alpha _3=\left(\begin{array}{c}-1 \\ 1 \\ -3\end{array}\right) α 1 = 1 0 1 , α 2 = 2 1 − 1 α 3 = − 1 1 − 3 R 3 R ^3 R 3 β = ( 2 − 1 6 ) \beta=\left(\begin{array}{c}2 \\ -1 \\ 6\end{array}\right) β = 2 − 1 6 α 1 , α 2 , α 3 \alpha _1, \alpha _2, \alpha _3 α 1 , α 2 , α 3 R 3 R ^3 R 3 α 1 , α 2 , α 3 \alpha _1, \alpha _2, \alpha _3 α 1 , α 2 , α 3 ( α 1 , α 2 , α 3 ) ∼ E \left( \alpha _1, \alpha _2, \alpha _3\right) \sim E ( α 1 , α 2 , α 3 ) ∼ E β \beta β x 1 , x 2 , x 3 x_1, x_2, x_3 x 1 , x 2 , x 3 ( α 1 , α 2 , α 3 ) ( x 2 x 2 x 3 ) = β \left( \alpha _1, \alpha _2, \alpha _3\right)\left(\begin{array}{l}x_2 \\ x_2 \\ x_3\end{array}\right)= \beta ( α 1 , α 2 , α 3 ) x 2 x 2 x 3 = β A x = β A x = \beta A x = β ( A ∣ β ) ( A \mid \beta ) ( A ∣ β ) A A A E E E α 1 , α 2 , α 3 \alpha_1, \alpha_2, \alpha_3 α 1 , α 2 , α 3 R 3 R ^3 R 3 A A A E E E β \beta β x = A − 1 β x=A^{-1} \beta x = A − 1 β
( A ∣ β ) = ( 1 2 − 1 2 0 1 1 − 1 1 − 1 − 3 6 ) → ( 1 2 − 1 2 0 1 1 − 1 0 − 3 − 2 4 ) → ( 1 2 − 1 2 0 1 1 − 1 0 0 1 1 ) → ( 1 0 0 7 0 1 0 − 2 0 0 1 1 ) . ( A \mid \beta )=\left(\begin{array}{ccc|c}
1 & 2 & -1 & 2 \\
0 & 1 & 1 & -1 \\
1 & -1 & -3 & 6
\end{array}\right) \rightarrow\left(\begin{array}{ccc|c}
1 & 2 & -1 & 2 \\
0 & 1 & 1 & -1 \\
0 & -3 & -2 & 4
\end{array}\right) \rightarrow\left(\begin{array}{ccc|c}
1 & 2 & -1 & 2 \\
0 & 1 & 1 & -1 \\
0 & 0 & 1 & 1
\end{array}\right) \rightarrow\left(\begin{array}{ccc|c}
1 & 0 & 0 & 7 \\
0 & 1 & 0 & -2 \\
0 & 0 & 1 & 1
\end{array}\right) . ( A ∣ β ) = 1 0 1 2 1 − 1 − 1 1 − 3 2 − 1 6 → 1 0 0 2 1 − 3 − 1 1 − 2 2 − 1 4 → 1 0 0 2 1 0 − 1 1 1 2 − 1 1 → 1 0 0 0 1 0 0 0 1 7 − 2 1 . 因为 A = ( α 1 , α 2 , α 3 ) ∼ E A=\left( \alpha _1, \alpha _2, \alpha _3\right) \sim E A = ( α 1 , α 2 , α 3 ) ∼ E α 1 , α 2 , α 3 \alpha _1, \alpha _2, \alpha _3 α 1 , α 2 , α 3 R 3 R ^3 R 3 β = ( 2 − 1 6 ) \beta =\left(\begin{array}{c}2 \\ -1 \\ 6\end{array}\right) β = 2 − 1 6 ( 7 − 2 1 ) \left(\begin{array}{c}7 \\ -2 \\ 1\end{array}\right) 7 − 2 1
例 所有二阶实方阵构成的实线性空间 R 2 × 2 R ^{2 \times 2} R 2 × 2
E 11 = ( 1 0 0 0 ) , E 12 = ( 0 1 0 0 ) , E 21 = ( 0 0 1 0 ) , E 22 = ( 0 0 0 1 ) , E _{11}=\left(\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right), \quad E _{12}=\left(\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right), \quad E _{21}=\left(\begin{array}{ll}
0 & 0 \\
1 & 0
\end{array}\right), \quad E _{22}=\left(\begin{array}{ll}
0 & 0 \\
0 & 1
\end{array}\right), E 11 = ( 1 0 0 0 ) , E 12 = ( 0 0 1 0 ) , E 21 = ( 0 1 0 0 ) , E 22 = ( 0 0 0 1 ) , 试证明 E 11 , E 12 , E 21 , E 22 E _{11}, E _{12}, E _{21}, E _{22} E 11 , E 12 , E 21 , E 22 R 2 × 2 R ^{2 \times 2} R 2 × 2
η = ( a b c d ) ∈ R 2 × 2 \eta =\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right) \in R ^{2 \times 2} η = ( a c b d ) ∈ R 2 × 2 在基 E 11 , E 12 , E 21 , E 22 E _{11}, E _{12}, E _{21}, E _{22} E 11 , E 12 , E 21 , E 22 k 1 , k 2 , k 3 , k 4 k_1, k_2, k_3, k_4 k 1 , k 2 , k 3 , k 4 k 1 E 11 + k 2 E 12 + k 3 E 21 + k_1 E _{11}+k_2 E _{12}+k_3 E _{21}+ k 1 E 11 + k 2 E 12 + k 3 E 21 + k 4 E 22 = O k_4 E _{22}= O k 4 E 22 = O
k 1 ( 1 0 0 0 ) + k 2 ( 0 1 0 0 ) + k 3 ( 0 0 1 0 ) + k 4 ( 0 0 0 1 ) = O . k_1\left(\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right)+k_2\left(\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right)+k_3\left(\begin{array}{ll}
0 & 0 \\
1 & 0
\end{array}\right)+k_4\left(\begin{array}{ll}
0 & 0 \\
0 & 1
\end{array}\right)= O . k 1 ( 1 0 0 0 ) + k 2 ( 0 0 1 0 ) + k 3 ( 0 1 0 0 ) + k 4 ( 0 0 0 1 ) = O . 那么显然,只能有 k 1 = k 2 = k 3 = k 4 = 0 k_1=k_2=k_3=k_4=0 k 1 = k 2 = k 3 = k 4 = 0 E 11 , E 12 , E 21 , E 22 E _{11}, E _{12}, E _{21}, E _{22} E 11 , E 12 , E 21 , E 22
η = ( a b c d ) ∈ R 2 × 2 \eta =\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right) \in R ^{2 \times 2} η = ( a c b d ) ∈ R 2 × 2 可表示为 η = a E 11 + b E 12 + c E 21 + d E 22 \eta =a E _{11}+b E _{12}+c E _{21}+d E _{22} η = a E 11 + b E 12 + c E 21 + d E 22 E 11 , E 12 , E 21 , E 22 E _{11}, E _{12}, E _{21}, E _{22} E 11 , E 12 , E 21 , E 22 R 2 × 2 R ^{2 \times 2} R 2 × 2 R 2 × 2 R ^{2 \times 2} R 2 × 2
η = ( a b c d ) ∈ R 2 × 2 \eta =\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right) \in R ^{2 \times 2} η = ( a c b d ) ∈ R 2 × 2 在这组基下的坐标是
x = ( a b c d ) . x =\left(\begin{array}{l}
a \\
b \\
c \\
d
\end{array}\right) . x = a b c d . 基、维数及其坐标的几何意义 在解析几何中,为了研究几何图形的变换,我们总是在一个固定的坐标系中讨论,进而把几何问题转化为代数问题。同样,在 n n n
对于向量空间 V V V { α 1 , α 2 , ⋯ , α n } \left\{\alpha_1, \alpha_2, \cdots, \alpha_n\right\} { α 1 , α 2 , ⋯ , α n }
α 1 , α 2 , ⋯ , α n \alpha_1, \alpha_2, \cdots, \alpha_n α 1 , α 2 , ⋯ , α n
V V V α \alpha α α 1 , α 2 , ⋯ , α n \alpha _1, \alpha _2, \cdots, \alpha _n α 1 , α 2 , ⋯ , α n α = x 1 α 1 + x 2 α 2 + … + x n α n \alpha =x_1 \alpha _1+x_2 \alpha _2+\ldots+x_n \alpha _n α = x 1 α 1 + x 2 α 2 + … + x n α n { α 1 , α 2 , ⋯ , α n } \left\{\alpha_1, \alpha_2, \cdots, \alpha_n\right\} { α 1 , α 2 , ⋯ , α n } V V V { α 1 , α 2 , ⋯ , α n } \left\{\alpha_1, \alpha_2, \cdots, \alpha_n\right\} { α 1 , α 2 , ⋯ , α n } n n n V V V ( x 1 , x 2 , ⋯ , x n ) \left(x_1, x_2, \cdots, x_n\right) ( x 1 , x 2 , ⋯ , x n ) α \alpha α { α 1 , α 2 , ⋯ , α n } \left\{ \alpha _1, \alpha _2, \cdots, \alpha _n\right\} { α 1 , α 2 , ⋯ , α n }
基的几何意义 基是向量空间的一组很 "结实" 的向量集合,每一个基向量可以像房屋地基的每一块石块,一样支撑衍生出空间中的全部向量。因此,首先一个基能代表或衍生出空间里的所有的向量,缺一不可; 其次, 作为基的每一个向量都是个顶个, 谁也不能代表谁, 它们必须线性无关, 它是一个极大无关向量组。
我们给一个向量空间找一个基,目的是为了给这个空间定一个坐标系,以方便我们定位和计算向量。一个基实际上就是选取的一个坐标系,另外一个基就是选取的一个新的坐标系。基是坐标系在线性空间中的推广。基向量对应坐标系的坐标轴,有几个基向量就有几个坐标轴, n n n n n n R n R ^n R n
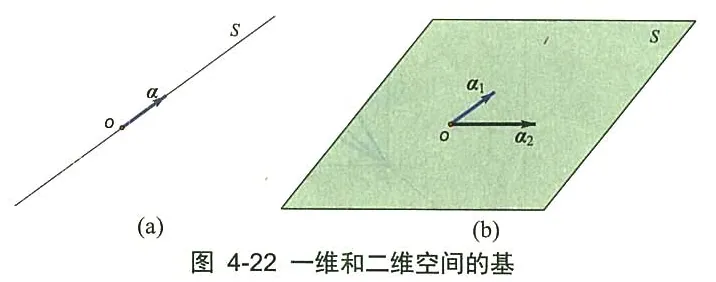
图 4-22(a)中,一维向量空间 S S S α 1 ≠ 0 \alpha _1 \neq 0 α 1 = 0 S S S S S S α \alpha α S = Span ( α ) S=\operatorname{Span}( \alpha ) S = Span ( α ) { α } \{ \alpha \} { α } S S S
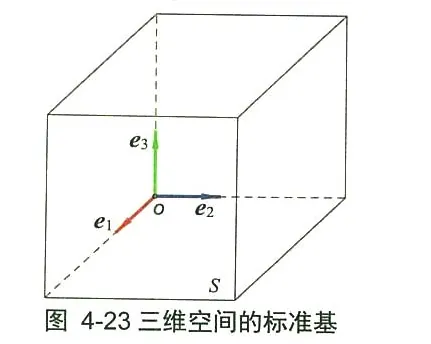
图 4-22 (b) 中, 如果二维向量空间 S S S R 3 R ^3 R 3 α 1 、 α 2 \alpha _1 、 \alpha _2 α 1 、 α 2 S S S { α 1 , α 2 } \left\{\alpha_1, \alpha_2\right\} { α 1 , α 2 } S S S α 1 、 α 2 \alpha _1 、 \alpha _2 α 1 、 α 2 S = Span { α 1 , α 2 } S=\operatorname{Span}\left\{ \alpha _1, \alpha _2\right\} S = Span { α 1 , α 2 } { α 1 , α 2 } \left\{ \alpha _1, \alpha _2\right\} { α 1 , α 2 } S S S R 3 R ^3 R 3 { e 1 , e 2 , e 3 } = : { ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) } \left\{ e _1, e _2, e _3\right\}=:\{(1,0,0),(0,1,0),(0,0,1)\} { e 1 , e 2 , e 3 } =: {( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 )} e 1 、 e 2 、 e 3 e_1 、 e_2 、 e_3 e 1 、 e 2 、 e 3 R 3 R ^3 R 3 { e 1 , e 2 , e 3 } \left\{e_1, e_2, e_3\right\} { e 1 , e 2 , e 3 } R 3 R ^3 R 3
坐标与维数的几何意义 一个基包含的向量个数就是坐标轴的个数,也就是向量空间的维数。维数是空间的一个本质特征,它不依赖于基的选取。选取不同的基,基向量的个数不会改变,维持支撑空间的维数不会改变。这就是为何称之为 "维数" 的原因。
一个向量空间的基选定后, 其坐标是什么?如何求取?下面我们接着看看几个图示的例子。
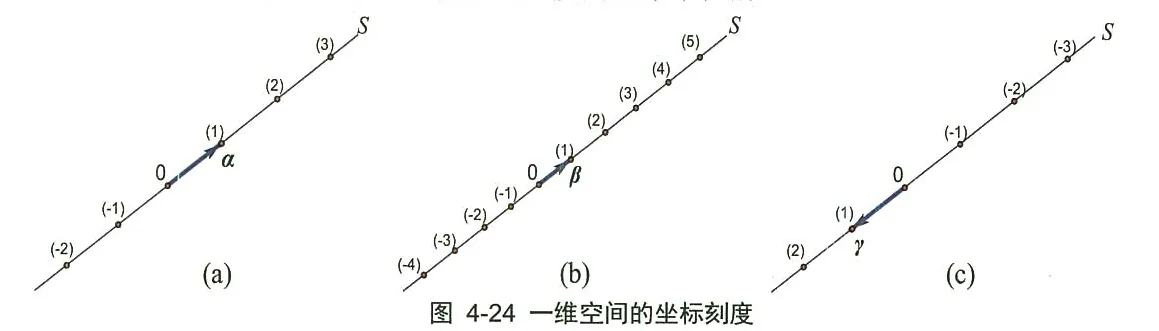
一维基及其坐标刻度 一维空间 S S S { α } \{ \alpha \} { α } β \beta β 0.5 α 0.5 \alpha 0.5 α γ \gamma γ − α - \alpha − α
显然,坐标轴的刻度是以所选基向量的长度为基本单位的。
二维基及其坐标刻度
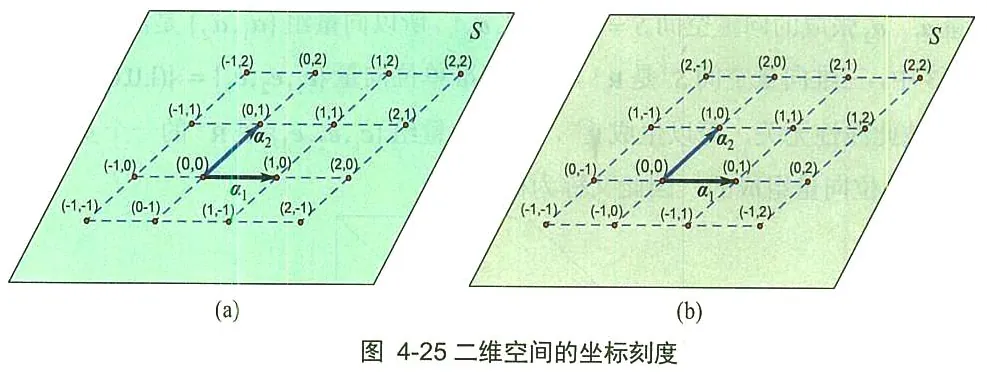
二维空间 S S S { α 1 , α 2 } \left\{\alpha_1, \alpha_2\right\} { α 1 , α 2 } α 1 、 α 2 \alpha_1 、 \alpha_2 α 1 、 α 2
另外, 在二维空间中, 确定基向量的顺序是必要的。在向量组的讨论中我们不强调向量组中向量们的顺序,但作为一个基的向量组就要有顺序了。显然,如果基向量的顺序进行了调整,坐标值也相应进行调整。在图 4-25(b)中,我们把图 4-25(a)的空间 S S S { α 1 , α 2 } \left\{ \alpha _1, \alpha _2\right\} { α 1 , α 2 } { α 2 , α 1 } \left\{\alpha_2, \alpha_1\right\} { α 2 , α 1 }
另外,我们在上述的例子中也看到了基与直角坐标系的不同,两个基向量不一定垂直;在刻画坐标网络时不是直角坐标系的垂直投影,而是平行四边形坐标网络,分割一个坐标轴的坐标线是与另外一个坐标轴平行的关系。一个基向量的方向是对应坐标轴的正方向,坐标单位是基向量的长度。
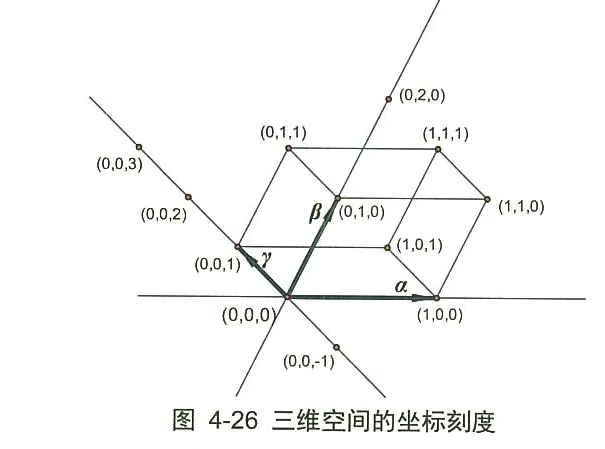
三维基及其坐标刻度 三维空间的一个基包含了三个线性无关的向量 { α , β , γ } \{ \alpha , \beta , \gamma \} { α , β , γ } α , β , γ \alpha , \beta , \gamma α , β , γ ( 1 , 1 , 1 ) (1,1,1) ( 1 , 1 , 1 )
下面对于一个三维空间中的二维子空间,我们看看它的基及其坐标是如何刻画的。
三维空间的子空间的基及其向量坐标 在图 4-26的三维空间的例子中, 设向量 a a a ( 1 , 1 , 0 ) (1,1,0) ( 1 , 1 , 0 ) { α , β } \{ \alpha , \beta \} { α , β } S = Span { α , β } S=\operatorname{Span}\{ \alpha , \beta \} S = Span { α , β } α 、 β \alpha 、 \beta α 、 β a a a S S S a a a ( 1 , 1 ) (1,1) ( 1 , 1 ) a a a Span { α , β , γ } \operatorname{Span}\{ \alpha , \beta , \gamma \} Span { α , β , γ } B B B ( 1 , 1 , 0 ) (1,1,0) ( 1 , 1 , 0 ) B = { α , β , γ } B =\{ \alpha , \beta , \gamma \} B = { α , β , γ } a a a Span { α , β } \operatorname{Span}\{ \alpha , \beta \} Span { α , β } B B B ( 1 , 1 ) (1,1) ( 1 , 1 ) B = { α , β } B =\{ \alpha , \beta \} B = { α , β }
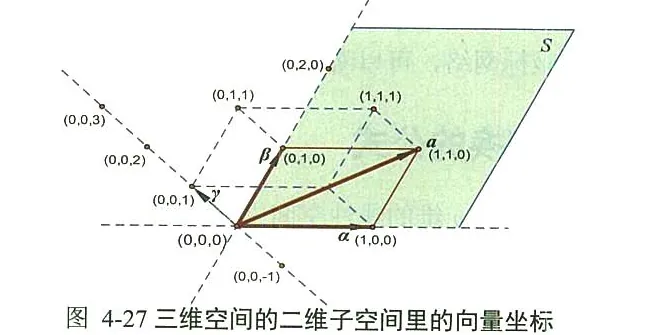 总结一下: 向量 在三维空间 中的 坐标是 , 其中 ; 而向量 在二维空间 中的 坐标变成了 ,其中 。
总结一下: 向量 在三维空间 中的 坐标是 , 其中 ; 而向量 在二维空间 中的 坐标变成了 ,其中 。