4._方程的向量表示及线性组合

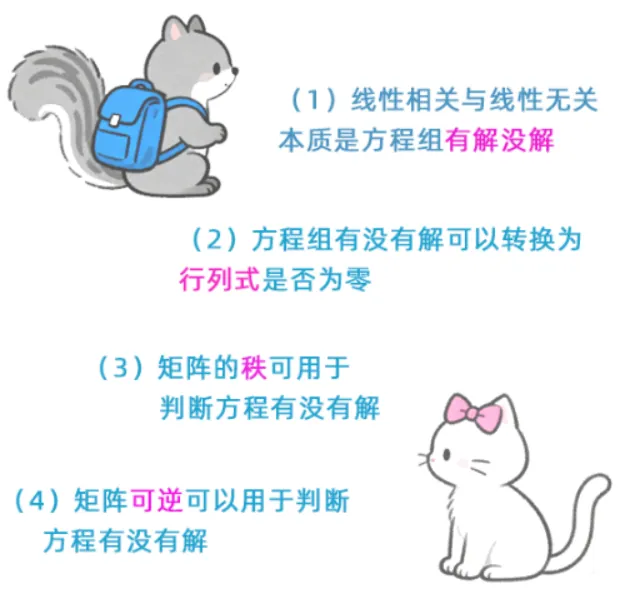
方程的向量表示

设有一个线性方程组

在矩阵章节里介绍，他们可以写成矩阵的方式 详见此处，即

方程除了可以用矩阵表示外，还可以用向量表示。设上面方程组的增广矩阵为

分别用 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n ; \boldsymbol{\beta}$ 表示上述矩阵的列向量, 即

注意：我们默认总是使用列向量

则上面方程组等价于下列向量形式的方程式:

即

这个式子告诉我们，求解一次线性方程组的解，既可以采用“矩阵”的视角，又可以采用“向量”的视角。

如果把(◆) 两边取转置，并根据转置的线性性质就可以得到

通过上面可以看到，矩阵的行与列本质是相同的。

如果我们把$\boldsymbol{a_1}$、 $\boldsymbol{a_2}$ ... $\boldsymbol{a_n}$ 当初坐标系（也就是基），那么其值$\boldsymbol{x}= (x_1,x_2,...x_n)^T$ 就可以看成在该坐标系下的坐标值。

理解一个方程的三种叫法

对于方程 $AX=B$，有三种叫法。 ①方程的叫法是 $AX=B$ （方程有解，矩阵的秩和增广矩阵的秩相等）

②矩阵的的叫法是矩阵$A$乘以矩阵$X$ 等于矩阵 $B$

③写成向量是$\alpha,x$可以线性表示向量$\beta$ (线性相关)。

向量组及其线性组合

我们知道，在平面上的两个二维向量 $\boldsymbol{\alpha}$ 和 $\boldsymbol{\beta}$ ，若存在一常数 $k$ ，使得

则常称向量 $\boldsymbol{\alpha}$ 与 $\boldsymbol{\beta}$ 成比例．例如，

则 $\boldsymbol{\alpha}=\frac{1}{2} \boldsymbol{\beta}$ ． 将这个概念推广到有限多个 $n$ 维向量

定义1 给定 $n$ 维向量组 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n$ ，对于任意一组数 $k_1, k_2, \cdots, k_n$ ，表达式 $k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+\cdots+k_n \boldsymbol{\alpha}_n$ 称为该向量组的一个线性组合.

比如 (这里直接使用行向量转置T表示)

那么 $2 \boldsymbol{\alpha}_1+4 \boldsymbol{\alpha}_2+7 \boldsymbol{\alpha}_3+ 6 \boldsymbol{\alpha}_4$ 成为向量组的一个线性组合。

定义2 给定 $n$ 维向量组 $\alpha_1, \alpha_2, \cdots, \alpha_n$ 和一个 $n$ 维向量 $\beta$ ，如果存在一组数 $k_1, k_2, \cdots, k_n$ ，使得

则称向量 $\beta$ 可由向量组 $\alpha_1, \alpha_2, \cdots, \alpha_n$ 线性表示，或者说向量 $\beta$ 是向量组 $\alpha_1, \alpha_2, \cdots, \alpha_n$ 的一个线性组合.

例如，上面给定向量组 $\alpha_1, \alpha_2, \alpha_3$ ，则向量

都是向量组 $\alpha_1, \alpha_2, \alpha_3$ 的线性组合. 由此可见，一个向量组可以线性表示这个向量组中的每一个向量， 零向量是任意一个向量组的线性组合.

例 设向量组 $\boldsymbol{e}_1=\left(\begin{array}{l}1 \\ 0 \\ \vdots \\ 0\end{array}\right), \boldsymbol{e}_2=\left(\begin{array}{l}0 \\ 1 \\ \vdots \\ 0\end{array}\right), \cdots, \boldsymbol{e}_n=\left(\begin{array}{l}0 \\ 0 \\ \vdots \\ 1\end{array}\right)$ ，则任一向量 $\boldsymbol{\alpha}=\left(\begin{array}{c}a_1 \\ a_2 \\ \vdots \\ a_n\end{array}\right)$ 都可由 $e_1, e_2, \cdots, e_n$ 线性表示， 即 $\boldsymbol{\alpha}=\left(\begin{array}{c}a_1 \\ a_2 \\ \vdots \\ a_n\end{array}\right)=a_1\left(\begin{array}{l}1 \\ 0 \\ \vdots \\ 0\end{array}\right)+a_2\left(\begin{array}{l}0 \\ 1 \\ \vdots \\ 0\end{array}\right)+\cdots+a_n\left(\begin{array}{l}0 \\ 0 \\ \vdots \\ 1\end{array}\right)=a_1 \boldsymbol{e}_1+a_2 e_2+\cdots+a_n \boldsymbol{e}_n$.

我们把$(e_1,e_2,...e_n)$称作 n维单位向量，也称作n维基向量，或者称作标准笛卡尔坐标基。

而这里的$(a_1,a_2...a_n)$ 可以当做坐标值理解。

及时总结

{width=400px}

说明：

• 行列式的值：决定了矩阵 $A$ 是否可逆。如果 $\det(A) \neq 0$，则 $A$ 可逆；如果 $\det(A) = 0$，则 $A$ 不可逆。

• 线性相关/无关：如果列向量线性无关，则 $\det(A) \neq 0$；如果线性相关，则 $\det(A) = 0$。

• 齐次方程组：总是有解（零解），但当 $\det(A) = 0$ 时，还有非零解（无穷多解）。

• 矩阵的值：如果是满秩只有零解，线性无关，否则线性相关。

定理

在本文一开始介绍的方程里，方程(★)的表达方式为

而在线性组合的定义为

可以发现这2个形式本质上是一样的。因此可以得到如下定理

向量 $\beta$ 可由向量组 $\alpha_1, \alpha_2, \cdots, \alpha_n$ (唯一) 线性表示的充分必要条件是线性方程组 $x_1 \alpha_1+x_2 \alpha_2+\cdots+x_n \boldsymbol{\alpha}_n=\beta$ 有 (唯一) 解.

证明 如果向量 $\beta$ 可由向量组 $\alpha_1, \alpha_2, \cdots, \alpha_n$ 线性表示，则存在一组数 $k_1, k_2, \cdots, k_n$ ，使得

这表明线性方程组 $x_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+\cdots+x_n \boldsymbol{\alpha}_n=\boldsymbol{\beta}$ 有解

反之，如果线性方程组

有解

即 $k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+\cdots+k_n \boldsymbol{\alpha}_n=\boldsymbol{\beta}$ ， 从而向量 $\beta$ 可由向量组 $\alpha_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n$ 线性表示.

例 设有向量 $\boldsymbol{\alpha}=\left(\begin{array}{c}5 \\ 3 \\ -6\end{array}\right)$ 及向量组 $\beta_1=\left(\begin{array}{l}1 \\ 1 \\ -1\end{array}\right) \boldsymbol{\beta}_2=\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right) \boldsymbol{\beta}_3=\left(\begin{array}{l}-1 \\ 1 \\ 2 \\ 2\end{array}\right)$, 试问 $\boldsymbol{\alpha}$ 能否由 $\beta_1, \boldsymbol{\beta}_2, \beta_3$ 线性表示.

解 设 $x_1 \beta_1+x_2 \beta_2+x_3 \beta_3=\alpha$ ，由 可知方程组有无穷多解: $\left\{\begin{array}{l}x_1=5+c, \\ x_2=-1-c, \\ x_3=c\end{array}\right.$, 其中 $c$ 为任意常数. 因此 $\boldsymbol{\alpha}$ 能由 $\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_{\mathbf{3}}$ 线性表示, 且表示式不唯一: $\alpha=(5+c) \boldsymbol{\beta}_1+(-1-c) \boldsymbol{\beta}_2+c \boldsymbol{\beta}_3$ ，其中 $c$ 为任意常数.

例设向量组 $\boldsymbol{\alpha}_1=\left(\begin{array}{c}1 \\ 0 \\ -2\end{array}\right), \boldsymbol{\alpha}_2=\left(\begin{array}{c}2 \\ 1 \\ -5\end{array}\right), \boldsymbol{\alpha}_3=\left(\begin{array}{c}-3 \\ 2 \\ 4\end{array}\right) ，$ 而 $\boldsymbol{\beta}=\left(\begin{array}{c}5 \\ 4 \\ -7\end{array}\right)$ ，问：向量 $\boldsymbol{\beta}$ 能否由向量组 $\alpha_1, \alpha_2, \alpha_3$ 线性表示？若可以，求出线性表达式。

解 设 $x_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+x_3 \boldsymbol{\alpha}_3=\boldsymbol{\beta}$ ，由

可知线性方程组无解，所以向量 $\beta$ 不能由向量组 $\alpha_1, \alpha_2, \alpha_3$ 线性表示.

上面解法可能有些同学看不懂，这里给出简单解释：给你一组向量$a_i$，判断他能否表示另外一个（或一组）向量$b_j$，基本思想是把$a_i,b_j$组成一个大矩阵，然后进行初等行变换，化为阶梯形矩阵，然后判断方程组有没有解（上面说过对向量的表示就是求方程组的解）。如何判断方程组有没有解就看矩阵的秩和增广矩阵的秩是否相等。如果相等则表示方程有解，可以线性表示。否则表示无解，线性无关。

以上面例子为例，最后一行化简后为 $0,0,0,7$ 还原方程为 $0x_1+0 x2+0 x_3=7$ 这显然不可能的，所以，方程组无解,也就是$a_i$无法表示$b_j$

在矩阵介绍过，方程的解可以用矩阵的秩判断，详见 矩阵的秩与方程的解 因此，我们就可以得到下面一个推论

$n$ 维向量 $\boldsymbol{\beta}$ 可由向量组 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m$ 线性表示的充分必要条件为 $r(\boldsymbol{A})=r({\boldsymbol{A|\beta}})$ ①$\boldsymbol{\beta}$ 可由 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots$ ， $\boldsymbol{\alpha}_m$ 线性表示且表示系数唯一的充分必要条件是 $r(\boldsymbol{A})=r({\boldsymbol{A|\beta}})= \boldsymbol{m}$ ②$\boldsymbol{\beta}$ 可由 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m$ 线性表示且表示系数不唯一的充分必要条件是 $r(\boldsymbol{A})=r({\boldsymbol{A|\beta}})<m$ ③$\boldsymbol{\beta}$ 不能由 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m$ 线性表示的充分必要条件是 $r(\boldsymbol{A}) \neq r({\boldsymbol{A|\beta}})$

例 令 $\alpha _1=\left[\begin{array}{c}1 \\ -2 \\ -5\end{array}\right], \alpha _2=\left[\begin{array}{l}2 \\ 5 \\ 6\end{array}\right], \beta =\left[\begin{array}{c}7 \\ 4 \\ -3\end{array}\right], \beta$ 能否写成 $\alpha _1$ 和 $\alpha _2$ 的线性组合？ 解 根据定义，问题即判断向量方程

是否有解，即

利用初等行变换将增广矩阵化成行最简形：

上面矩阵（5）还原为方程就是

所以（5）的解是 $x_1=3, x_2=2$ ．因此 $\beta$ 可以写成 $\alpha _1$ 和 $\alpha _2$ 的线性组合，即

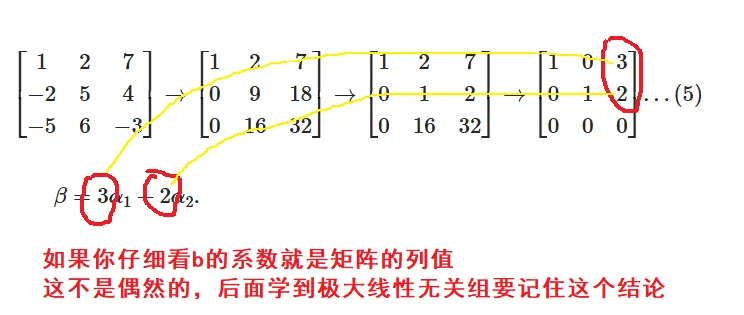
综合运用

例 设向量

讨论 $a, b$ 为何值时， $\beta$ 不能由 $\alpha_1, \alpha_2, \alpha_3$ 线性表示？$a, b$ 为何值时， $\beta$ 可由 $\alpha _1, \alpha _2, \alpha _3$ 线性表示？并写出所有的表示式．

解：令

显然，当 $b \neq-1$ 时，$r( A ) \neq r(\tilde{ A })$ ，线性方程组 $A x = \beta$ 无解，故 $\beta$ 不能由 $\alpha _1, \alpha _2, \alpha _3$ 线性表示；

当 $b=-1, a \neq-2$ 时，$r( A )=$ $r(\tilde{ A })=3$ ，线性方程组 $A x = \beta$ 有唯一解 $x_1=0, x_2=7, x_3=-1$ ，故 $\beta$ 可由 $\alpha _1, \alpha _2, \alpha _3$ 线性表示，且表示系数唯一，表示式为

当 $b=-1, a=-2$ 时，$r( A )=r(\tilde{ A })=2<3$ ，线性方程组 $A x = \beta$有无穷多解，其解为

故 $\beta$ 可由 $\alpha _1, \alpha _2, \alpha _3$ 线性表示，且表示式有无穷多，其表示式为 $\beta =-\left(\frac{1}{2}+\frac{1}{2} k\right) \alpha _1+(5-2 k) \alpha _2+k \alpha _3, k$ 为任意常数．

上面这个例题非常典型，考生必须掌握

例设向量组 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m$ 为 $n$ 维向量组，证明：向量组中每一向量都可由 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m$ 线性表示．

证明：任取 $\boldsymbol{\alpha}_i, 1 \leqslant i \leqslant m$ ，有